Re tout le monde,
Bon je n’aurais pas le temps de créer un Github ce soir , je poste le code ici (dans un premier temps)^^!
Fonction qui teste toutes les combinaisons de poids
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | def computeAllPossibleInterpolatedPoints(step : Double, points : Seq[Seq[Double]], transform: (Double) => Double) : Seq[Seq[Double]] = {
var returned_object : Seq[Seq[Double]] = Seq.empty[Seq[Double]]
recursiveInterpolation(0, Seq.empty[Double])
def recursiveInterpolation(current_weight_id : Int, building_weights : Seq[Double]) : Unit = {
(.0 to 1.0 by step).foreach(current_step => {
if (current_weight_id < points.size - 1) {
recursiveInterpolation(current_weight_id + 1, building_weights :+ current_step)
} else {
val found_solution = (building_weights :+ current_step).map(transform)
if(Math.abs(found_solution.sum - 1.0) < 0.01) {
returned_object = returned_object :+ interpolation(found_solution, points)
}
}
})
}
returned_object
}
|
Comme vous le savez déjà, j’utilise la récursivité. Dans chaque appel récursif, j’itère de 0 à 1 sur chaque poids. Dès qu’une itération est exécutée, l’appel récursif est lancé. Au final ça signifie que je teste bien toutes les combinaisons possibles.
On a déjà dit que c’était gourmand en CPU et RAM et que des solutions alternatives étaient mieux en tout cas pour le CPU et probablement pour la RAM, on a aussi dit que certains points interpolés sont présents en doublons. Mais ces problèmes sont secondaires et ne concernent pas ma question initiale (qui est de savoir pourquoi je n’obtiens pas une jolie face interpolée avec cosinus).
if(Math.abs(found_solution.sum - 1.0) < 0.01) { permet de savoir si j’ai trouvé une combinaison valide (i.e. : dont la somme des poids vaut 1). Attention, ce test est mieux que de tester si la somme est égale à 1 par rapport à l’imprécision due aux chiffres après la virgule, pour l’interpolation cosinus.
transform peut être linear ou cosine.
Fonctions linear et cosine
| def linear(weight : Double) : Double = {
weight
}
def cosine(weight : Double) : Double = {
(1 - Math.cos(weight * Math.PI)) * 0.5
}
|
Fonction d’interpolation entre n points de k coordonnées
Cette fonction est utilisée par exemple par la fonction computeAllPossibleInterpolatedPoints.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20 | def interpolation(weights: Seq[Double], points: Seq[Seq[Double]], transform: (Double) => Double = null) : Seq[Double] = {
var transformed_weights = weights
if(transform != null) {
transformed_weights = weights.map(transform)
}
if(Math.abs(transformed_weights.sum - 1.0) >= 0.01) {
println("ERROR : `SUM(weights) != 1`. Returning `null`.")
return null
}
if(transformed_weights.exists(weight => BigDecimal(weight).setScale(5, BigDecimal.RoundingMode.HALF_UP).toDouble < 0)
||
transformed_weights.exists(weight => BigDecimal(weight).setScale(5, BigDecimal.RoundingMode.HALF_UP).toDouble > 1)) {
println("ERROR : `EXISTS(weight) / weight < -1 OR weight > 1`. Returning `null`.")
return null
}
transformed_weights.zip(points).map(
weight_point => weight_point._2.map(coordinate => weight_point._1 * coordinate)
).reduce((point_a : Seq[Double], point_b : Seq[Double]) => point_a.zip(point_b).map(coordinate_points => coordinate_points._1 + coordinate_points._2))
}
|
-
Remarquez que lorsqu’elle est appelée par computeAllPossibleInterpolatedPoints , aucun transform ne lui est passée en paramètre (regardez l’appel dans le code de computeAllPossibleInterpolatedPoints), et c’est bien logique : computeAllPossibleInterpolatedPoints applique déjà dans son code une transformation (soit cosine , soit linear).
-
On retrouve le test de la somme = 1
-
On trouve un autre test : tout poids doit être compris entre 0 et 1 tous deux inclus
-
J’ai écrit une petite succession de map et de reduce qu’on aime bien en Scala. Ce que ça fait, c’est tout bête : on multiplie chaque coordonnée de chaque point par le poids associé au point (l’ensemble des points est en effet en bijection avec l’ensemble des poids au niveau des paramètres, enfin on part de ce principe… à l’utilisateur de cette fonction de s’en assurer). Le point résultant de la somme de ces multiplications poids-coordonnées_de_point est retourné.
Exécutable
Vous pouvez tester ces fonctions avec ceci :
val more_points_0 : Seq[Seq[Int]] = interpolator.computeAllPossibleInterpolatedPoints(0.05, Seq(Seq(22, 22, 22, 1), Seq(33, 33, 33, 1), Seq(1, 1, 1, 1), Seq(52, 52, 52, 1)), interpolator.linear).map(_.map(_.intValue()))
Je viens de choisir ces coordonnées de manière totalement aléatoire parce qu’il faut que j’y aille ! 
Changez interpolator.linear par interpolator.cosine pour changer d’interpolation. interpolator est une instance de la classe Interpolator qui contient les fonctions ci-dessus.
Merci d’avance !
Eh oui ! Merci d’avance, encore, pour votre aide ! Je vous filerai dès que possible (demain matin et/ou après-midi) un exécutable (projecteur 3D + interpolations de face, l’objectif à terme étant d’utiliser du bruit pour donner une couleur/du volume à chaque face du cube).
Je compte faire un dépôt git auquel on pourra accéder via github.




 Une interpolation, ça se calcule directement. Si ton but est de comprendre les interpolations, il me semblerait plus utile d’écrire un code d’interpolation, pas un code de recherche dans l’espace des combinaisons linéaires…
Une interpolation, ça se calcule directement. Si ton but est de comprendre les interpolations, il me semblerait plus utile d’écrire un code d’interpolation, pas un code de recherche dans l’espace des combinaisons linéaires…
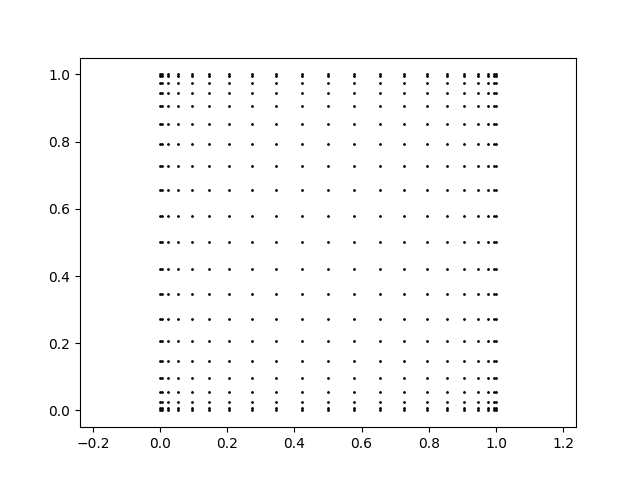
 Pour adapter ça à un quadrilatère quelconque, il faut bien évidemment déformer le résultat obtenu.
Pour adapter ça à un quadrilatère quelconque, il faut bien évidemment déformer le résultat obtenu.