Hello !
Je ne sais pas si tu connais beaucoup de théorie des représentations donc je vais essayer de rappeler un peu comment on peut voir tout ça.
Le groupe que l’on considère ici est S3 (le C3v chez toi), le groupe des permutations (ou groupe symétrique) d’un ensemble à trois éléments. Si je note {1,2,3} cet ensemble, alors S3={id,(12),(23),(13),(123),(132)} où les éléments sont des cycles (id est l’identité qui ne change rien). Par exemple, (123) agit en envoyant 1 sur 2, 2 sur 3 et 3 sur 1.
Une représentation (complexe) de ce groupe est un morphisme S3→GLn(C), c’est à dire qu’on associe à chaque élément de S3 un automorphisme d’un espace vectoriel de dimension n (de manière sympathique pour conserver les lois des groupes). Le caractère d’une telle représentation est simplement la trace de la matrice associée (via le morphisme) à un élément de S3. (Comme Tr(ghg−1)=Tr(g−1gh) =Tr(g)=Tr(h), ce caractère ne dépend que de la classe de conjugaison d’un élément, ce sont les colonnes dans la table.)
Les lignes de la table de caractères sont les valeurs des caractères irréductibles pour chaque classe de conjugaison (colonne). On est irréductible si on "mélange bien" tout l’espace sur lequel on agit, c’est-à-dire si il n’y a pas de sous espace strict qui soit stable sous tout les automorphismes.
Par exemple, dans le cas de la phrase que tu as du mal à comprendre (celle sur les matrices 2x2) : la troisième ligne de ton tableau est celle d’une représentation irréductible de degré 2, c’est à dire que le caractère est celui d’un morphisme S3→GL2(C), d’où les matrices 2x2, ie les "opérations bidimensionnelles".
Avant de me perdre dans mes explications bancales, je vais peut être répondre directement à tes questions :
- Le +2 est effectivement en relation directe avec le fait que C3v=S3 n’est pas abélien : si un groupe fini est abélien alors ses représentations irréductibles sont de dimension 1, et inversement, si il n’a que des représentations irréductibles de dimension 1 alors il est abélien. Le premier sens est un corollaire du lemme de Schur, le second est le simple fait que la somme des carrés des dimensions des représentations irréductibles est égale au cardinal de ton groupe.
Si on voulait dresser la table de S3 nous-mêmes, on pourrait procéder ainsi :
- on a trois classes de conjugaison, donc 3 colonnes et 3 lignes (c’est une proposition que le nombre de représentations irréductibles est égal au nombre de classes de conugaison),
- la première ligne est facile : c’est la représentation triviale (on envoie tout sur l’identité),
- la seconde est sympathique aussi : on prend le caractère donné par la signature d’une permutation,
- la troisième ligne peut se compléter avec des relations d’orthogonalité.
Je voudrais quand même expliciter géométriquement le troisième caractère.
On fait agit S3 sur C3 en permutant les coordonnées des triplets : par exemple (12)⋅(z1,z2,z3)=(z2,z1,z3). Cette représentation n’est pas irréductible : le droite Vect(1,1,1)={(z,z,z)∈C3} est stable (permuter les coordonnées égales ne change rien). On prend un supplémentaire H⊂C3 (tel que C3=H⊕C(1,1,1)).
On restreint alors notre attention sur H, de dimension 2 (le fameux "truc bidimentionnel").
J’espère ne pas trop m’être perdu.
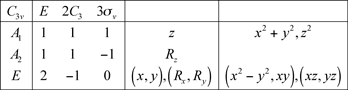







 Plus sérieusement merci pour vos réponses, j’imagine que je reviendrais vous embêter encore avec ces histoires. Les partiels de janvier toussa toussa
Plus sérieusement merci pour vos réponses, j’imagine que je reviendrais vous embêter encore avec ces histoires. Les partiels de janvier toussa toussa 

