Étude de la convergence d'une série

Bonjour à tous !

J’étudie la convergence de la série suivante avec $x \in \mathbb R$ :

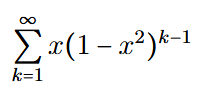
Selon mon corrigé, le domaine de convergence de la série est $D = \ ]-\sqrt{2}, \sqrt{2} \ [$
Je ne suis pas d’accord : pour $x = 1$, le premier terme de la série n’est pas défini et « vaut » : $0^0$.

Pour moi, le bon domaine de convergence est donc $D' = D - \{-1, 1\}$

Qu’en pensez-vous ?

Si je ne me trompe pas, tu peux être capable de faire une étude du domaine par morceaux sur les intervalles où tout est proprement défini. Ensuite étudier aux bornes de x = 1 ou -1 pour constater la continuité.

Ce n’est pas parce qu’il y a des parties du domaine avec des valeurs indéfinies que la continuité n’existe pas. Cela demande juste plus de travail pour s’assurer de la continuité aux bornes de ces valeurs limites.

Je ne comprends pas très bien. On m’a appris qu’une fonction est continue en un point si la fonction est définie en ce point et que les limites à droite/à gauche de ce point existent.

Tu as raison sur ce point, mais le problème n’est pas là.

La forme 0 élevée à la puissance 0 n’est pas une valeur interdite en mathématiques ou pour les fonctions. Dans le cas de l’étude des limites par exemple, cela signifie seulement que tu ne peux pas utiliser des opérations de base sur les limites dans ce cas de figure. En somme, il faut travailler le calcul pour trouver la valeur de la limite qui correspond. Cela ne signifie pas que la valeur n’existe pas. D’ailleurs dans d’autres contextes que l’analyse en mathématiques, la valeur est considérée comme 1.

Avec une étude de continuité en ce point je pense qu’il y a moyen de montrer que ta fonction est continue sur l’ensemble du domaine de définition proposée par ta correction et que la fonction est donc parfaitement définie en tout point de ce domaine.

En effet, mais justement tu peux définir une nouvelle série qui est le prolongement par continuité.

Typiquement, prends la fonction $f(x) = \frac{sin(x)}{x}$ qui n’est pas définie en $0$. Cependant on sait que $lim_{x\rightarrow 0^-} f(x) = 1$ et de même $lim_{x\rightarrow 0^+} f(x) = 1$. On peut donc définir une nouvelle fonction $f'$

qui est alors continue.

Voilà tu peux normalement faire la même chose dans ton exo

Ils ont juste admis que $0^0 = 1$. Ce qui se défend. Mais en toute logique, on se fiche de la valeur de $0^0$, peu importe ce que ce calcul vaut, ça ne change pas le résultat (tant que c’est un nombre).

Assez d’accord avec le message de Ache. Quand on parle de la convergence d’une série, on s’intéresse à ce qui se passe quand n est grand. Uniquement.

Même si on s’intéressait à la série 1/n², pour n commençant à 0, il faudrait répondre que la série converge.

Pour la série 1/n², on pourrait quand même souligner qu’il y a une coquille dans l’énoncé, parce que là, 1/0², c’est clairement non défini. Mais il faut voir cela comme une coquille dans l’énoncé, et pas un argument pour dire que la série ne converge pas.

Mais est-ce que $0^0$, c’est comme $\dfrac{0}{0}$, une indétermination qui peut valoir n’importe quoi ?

ça me perturbe car si la série converge, comment en calculer la valeur de convergence avec une telle indétermination ?

Voici la bon réponse :à)