Il faudrait en effet clarifier les règles qui limites certaines zones à certaines années. En disant entre 2027 et 2036 : les zones 13, 20 et 14, est-ce que ça veux dire que seul ces zones-là peuvent être sélectionnés durant cette période (mais qu’elles peuvent être sélectionnés à d’autres années aussi)? Est-ce que ça veux dire qu’elles ne peuvent être sélectionnés que durant cette période, mais que d’autres zones peuvent aussi être sélectionnés durant cette période? Un combinaison des deux? Pareil pour 2021–2026 avec [27, 3, 44].
Pour l’instant, j’ai juste testé du brute force (générer 10000 listes aléatoires de manière gourmande) et regarder combien des zones ont étés sélectionnés.
Sans limiter certaines zone à certaines années, j’arrive facilement à 46 zones en 80 ans:
16, None, None, 29, None, 24, 48, 3, 52, 15, 14, 42, 44, 34, 13, 38, 27, 25, 45, None, None, None, None, None, None, None, None, 12, None, None, 10, 6, None, 21, None, 33, None, 2, 11, 49, 9, None, 51, 43, 32, 39, 26, 20, 47, None, None, None, None, None, None, None, None, 23, None, None, None, None, None, 28, None, 19, None, 4, 17, 5, 8, 7, 50, 46, None, 30, 22, 35, 36, None
En supposant que les limitations d’années-zones veulent dire qu’on ne peut sélectionner que ces zones durant la période (mais qu’on peut les sélectionner à d’autre moment aussi), j’arrive à 40 zones:
16, None, None, 29, None, 24, 44, 27, 3, None, None, None, 13, 14, None, None, None, None, None, None, None, None, 49, 45, 15, 34, 42, 38, 25, 7, 10, 12, None, 21, None, 33, 51, None, 4, 11, None, None, None, None, None, None, None, None, None, None, None, None, 48, None, None, 32, 26, 35, 30, 20, 9, 23, None, 28, 36, 19, 50, 52, 2, 18, 5, 6, None, None, None, None, None, None, None, None
En supposant que les limitations d’années-zones veulent dire qu’on ne peut sélectionner ces zones que durant la période (mais qu’on peut sélectionner d’autres zones aussi durant la période), j’arrive à 45 zones:
16, None, None, 29, None, 24, 38, 44, 3, 49, 18, 27, 34, 42, 45, 7, 14, 8, 20, None, None, None, None, None, None, None, None, None, None, None, 22, None, None, None, None, 23, 31, 30, 5, 4, 46, 50, 28, 48, 17, 35, 32, 36, 9, None, None, None, None, None, None, None, None, None, None, None, 26, None, None, None, None, 12, None, 25, 10, 2, 6, 52, 33, None, 11, 39, 43, 21, 15, 47
En supposant que les limitations d’années-zones veulent dire qu’on ne peut sélectionner ces zone que durant la période et que seules ces zones peuvent être sélectionnés durant la période, j’arrive à 39 zones:
16, None, None, 29, None, 24, 3, 44, 27, None, None, None, 14, 20, None, None, None, None, None, None, None, None, 45, 49, 7, 32, 18, 38, 42, 12, 10, 15, None, None, None, 33, 4, 51, 26, 28, None, None, None, None, None, None, None, None, None, None, None, None, None, 48, None, None, 17, 25, 43, 36, 39, 5, 23, 8, None, 19, 2, 50, 52, 22, 34, 6, None, None, None, None, None, None, None, None
Au pifomètre, je dirais qu’il n’est pas possible d’explorer de manière exhaustive l’espace des possibilités car ça prendrait trop de temps. En revanche, il est possible de calculer rapidement (et relativement facilement) certaines choses qui pourraient être utile pour construire des heuristiques. Par exemple, si on pouvait sélectionner plusieurs zone pour la même année, il est possible de calculer le nombre maximum de zones qui peuvent être sélectionnés en même temps (en respectant toutes les autres règles). Typiquement, c’est le genre de chose qui permet d’orienter le choix vers des zones qui vont moins bloquer les choix future.

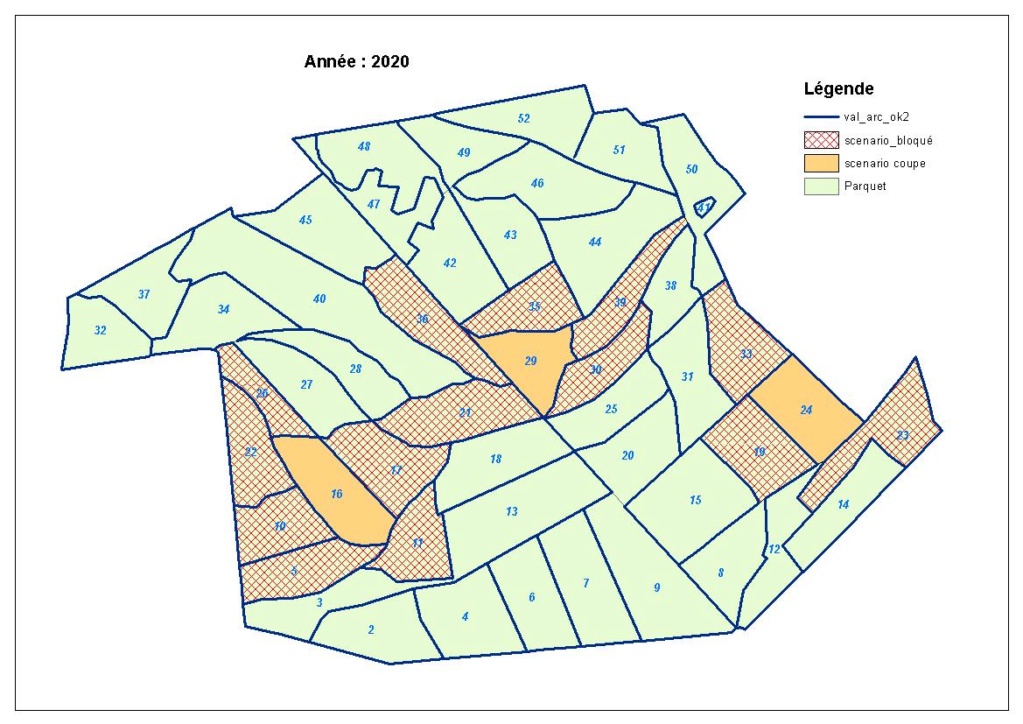
 Et oui c’est un cas réel, la carte représente bien les zones définies sur le terrain.
Et oui c’est un cas réel, la carte représente bien les zones définies sur le terrain.