Pendule Simple: Temps de parcours

Agrégation de science physique

Le problème exposé dans ce sujet a été résolu.

Bonjour à tous,

Comme vous le savez surement je prépare l’agrégation de sciences physique (option chimie). Dans le cadre de cet exercice compliqué j’ai du me rendre compte de mes limites en physiques… Surtout en mécanique. Je n’ai jamais eu de cours de mécanique (juste des corrections d’exercices en M1\text{M1} et là en M2\text{M2}).

Pendule simple

Une porte pousse une bille placée au bord sur une petite plateforme. La bille de masse m1m_1 est suspendue à un fil de longueur ℓ=30  cm\ell = 30\;cm fixé à un point O\text{O} situé à 29  cm29\;cm plus haut que la plateforme de départ de la bille. On supposera que le fil reste tendu en toute circonstance et que la rayon de la bille est négligeable.

Alors voilà comment je vois le problème :

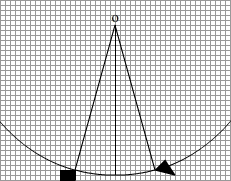
figure 1
figure 1

Un point O\text{O} situé à mis chemin entre le taquet et la plateforme de départ. La bille part de la plateforme de hauteur z=−29  cmz=-29\;cm le point du milieu est donc à z=−30  cmz=-30\;cm et frappe le taquet en z=−29  cmz=-29\;cm mais à l’autre bout.

Et la question est en gros : combien de temps Δt\Delta t met la bille à frapper le taquet ? Je pense qu’il faut accéder aux équations horaires et ainsi arriver à la période ?

Principe fondamental de la dynamique
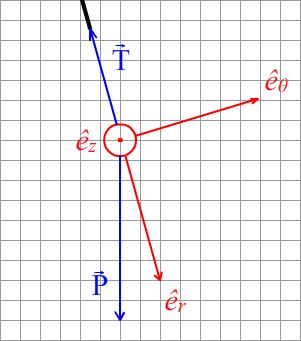
coordonnées cylindriques
coordonnées cylindriques
∑iFi,ext⃗=m1a⃗\sum_i \vec{\mathscr{F}_{i,ext}} = m_1\vec{a}
P⃗+T⃗=m1(araθaz)\vec{\mathscr{P}} + \vec{T} = m_1 \begin{pmatrix} a_r \\ a_\theta \\ a_z \end{pmatrix}
∣∣P⃗∣∣=P=m1g||\vec{\mathscr{P}}|| = \mathscr{P} = m_1g
P⃗=P(cos(θ)−sin(θ)0)\vec{\mathscr{P}} = \mathscr{P}\begin{pmatrix} cos(\theta) \\ -sin(\theta) \\ 0 \end{pmatrix}
∣∣T⃗∣∣=T||\vec{T}|| = T
P⃗=T(−100)\vec{\mathscr{P}} = T\begin{pmatrix} -1 \\ 0 \\ 0 \end{pmatrix}

Par identification j’obtiens :

m1aθ=−Psin(θ)m_1a_\theta = -\mathscr{P}sin(\theta)

Là je bloque sur l’expression de l’accéleration, alors je repars de la définition tel que MM point centré sur la bille :

{OM⃗=ℓer⃗v⃗=dOM⃗dta⃗=d2OM⃗dt2\left\{\begin{aligned} \vec{OM} &= \ell \vec{e_r} \\ \vec{v}&= \dfrac{d\vec{OM}}{dt} \\ \vec{a} &= \dfrac{d^2\vec{OM}}{dt^2} \end{aligned}\right.
dOM⃗dt=ℓdθdteθ⃗\dfrac{d\vec{OM}}{dt} = \ell \dfrac{d\theta}{dt} \vec{e_\theta}
d2OM⃗dt2=−ℓ(dθdt)2er⃗+ℓd2θdt2eθ⃗\dfrac{d^2\vec{OM}}{dt^2} = -\ell \left(\dfrac{d\theta}{dt}\right)^2 \vec{e_r} + \ell \dfrac{d^2\theta}{dt^2} \vec{e_\theta}
m1ℓd2θdt2=−m1gsin(θ)m_1 \ell \dfrac{d^2\theta}{dt^2} = -m_1gsin(\theta)

Sous forme canonique :

d2θdt2+gℓsin(θ)=0 \dfrac{d^2\theta}{dt^2} + \dfrac{g}{\ell}sin(\theta) = 0

Equation différentielle du second ordre si on se permet l’approximation des petits angles sinθ≈θsin\theta \approx \theta :

d2θdt2+gℓθ=0 \dfrac{d^2\theta}{dt^2} + \dfrac{g}{\ell}\theta = 0

Alors on reconnait le temps caractéristique suivant : ωo2=gℓ\omega_o^2 = \dfrac{g}{\ell} que l’on sait relier à la période T=2πωo=1.1  sT=\dfrac{2\pi}{\omega_o} = 1.1\;s… Ok c’est chose fait, ça nous aidera surement plus loin ?

A partir de là j’ai commencer à chercher la distance à parcourir sachant que l’altitude varie de 29  cm29\;cm à 30  cm30\;cm et à nouveau à 29  cm29\;cm alors j’ai pris α\alpha l’angle que fait la bille a début de l’expérience, avec la verticale:

cos(α)=29  cm30  cm⇔α=225πcos(\alpha) = \dfrac{29\;cm}{30\;cm} \Leftrightarrow \alpha = \dfrac{2}{25}\pi

Donc 2α=425π2\alpha = \dfrac{4}{25}\pi ce qui vaut le trajet du départ vers le milieu de la course, puis du milieu de la course vers le taquet… Ensuite le périmêtre (distance parcouru) peut-être calculé :

d=425π×30  cm=15.1  cmd = \dfrac{4}{25}\pi \times 30\;cm = 15.1\;cm

Et là je coince… Si je veux la durée de ce trajet, il me faut la vitesse mais c’est pas évident. l’idée que j’me donne c’est de prendre la dérivé de l’angle θ(t)↦dθ(t)dt\theta(t) \mapsto \dfrac{d\theta(t)}{dt} et donc de reprendre mon equation différentielle et la résoudre :

θ(t)=Aexp(ωot)+Bexp(−ωot)\theta(t) = Aexp(\omega_o t) + Bexp(-\omega_o t)

Or à l’instant initial t=0t=0 j’ai une information :

θ(0)=A+B=−α\theta(0) = A + B = -\alpha

La seconde information que j’ai, c’est la periodicité que je peux exprimer ainsi, si on néglige les forttements sur des petits angles, ce qui parrait cohérrent :

θ(T)=θ(2T)\theta(T) = \theta(2T)
Aexp(ωoT)+Bexp(−ωoT)=Aexp(ωo2T)+Bexp(−2ωoT)Aexp(\omega_o T) + Bexp(-\omega_o T) = Aexp(\omega_o 2T) + Bexp(-2\omega_o T)

J’obtiens que A=0A=0 et B=−αB=-\alpha

θ(t)=−225πexp(−ωot)\theta(t) = -\dfrac{2}{25} \pi exp(-\omega_o t)

Mais en fait malgré tout ça, j’me retrouve bloqué lorsque j’égalise :

v=dΔt=ℓdθdt=ℓωo225πexp(−ωot)v = \frac{d}{\Delta t} = \ell \dfrac{d\theta}{dt} = \ell \omega_o \dfrac{2}{25} \pi exp(-\omega_o t)

J’obtiens δt\delta t et tt j’ai du mal à voir comment j’peux m’en sortir. J’ai vraiment l’impression de ne pas être pertis du bon coté… Au risque de passer pour un aveugle, si quelqu’un pourrait me donner un indice ce serait cool. Ou alors j’me suis planté dans un calcul. Idem faite le moi savoir ^^

+0 -0

Si tu as la période, tu as ta réponse, vu que le pendule fait un demi battement et que la situation est symétrique…

Ceci dit, je pense qu’on attend aussi de justifier qu’on est bien dans un régime de petites oscillations, et d’estimer l’erreur par rapport à la solution exacte.

Après, et ça me paraîtrait logique pour l’agrégation, on n’est peut-être pas du tout dans des petits angles et il faut s’aventurer en terrain non linéaire. Il y a des infos sur Wikipedia à ce sujet.

Édit. : on est bien dans les petits angles, mais le cas non linéaire donne des informations sur la qualité de l’approximation.

+0 -0

Je doute qu’une combinaison d’exponentielles soit la solution.

ImperatorS79

Si si les coefficients des exponentielles sont complexes. Le terme imaginaire donne la pulsation et le terme réel donne l’amortissement (si negatif) ou l’amplification (si positif).

Le terme réel est donné par le terme du premier ordre ( dfdt\frac {\mathrm d f}{\mathrm d t}). Comme dans ce cas il n’y en a pas, il est nul et il n’y a ni amortissmenent, ni amplification (exp(0t)=exp(0)=1exp(0t) = exp(0)=1) : le mouvement est simplement periodique de type cos⁡(ωt+ϕ)\cos (\omega t + \phi).

+0 -0

Salut,

@Blackline : même si on se met dans le cas ou le taquet n’est pas nécessairement symétrique avec le point de départ (et est donc à une position angulaire plus proche de l’axe), je trouve que tu te prends beaucoup la tête à passer par la distance parcourue. Tout ce qui compte est l’angle, tu as une équation différentielle sur l’angle qu’on peut résoudre directement pour trouver θ=θ0cos⁡(ωt)\theta=\theta_0\cos(\omega t) avec ω=g/ℓ\omega=\sqrt{g/\ell} et θ0\theta_0 la position initiale. Une fois là, il est trivial de trouver l’instant t1t_1 auquel θ=θ1\theta=\theta_1 avec θ1\theta_1 la position du taquet : t1=1ωarccos⁡θ1θ0t_1=\frac 1\omega\arccos\frac{\theta_1}{\theta_0}. Pas la peine de passer par la vitesse intégrée sur le chemin quand l’angle suffit et qu’on a une équation dessus…

+0 -0

Et bah c’est bien mon problème. Me compliquer la tête pour rien et ne pas comprendre ce que je fais ! Merci à tous !

Merci beaucoup pour vos retours. J’ai aussi oublier de dire que c’est le sujet officiel de sciences physique (option chimie) de 2017 ! Je vais continuer à publier ma progression s’il y en a davantage :)

+0 -0

qu’on peut résoudre directement pour trouver θ=θocos(ωt)\theta = \theta_o cos(\omega t)

Comment tu fais ça ? J’ai du mal avec les equations différentielles du second ordre. A part apprendre par coeur que "la solution generale est une combinaison d’exponentielle" je ne sais pas trop comment on peut tomber sur cos(ωt)cos(\omega t) comme tu l’as fait ? J’aurais tendance à passer par les complexe pour me mettre en cosinus seulement dans une second temps à l’aide d’Euler…

EDIT :

Ok j’ai fais un peu de recherche et j’ai trouve (ici) une solution très interessante :

Solution détaillée
Solution détaillée

Mais certaines de ces étapes sont difficile à comprendre. Je vois bien qu’on essaye de trouver un facteur qui permet d’intégrer facielement l’équation notamment avec le 2dθ(t)dt2\dfrac{d\theta (t)}{dt}. Mais j’ai toujours pas les yeux en face des trous.

2dθ(t)dtd2θ(t)dt2=−2gℓθ(t)2dθ(t)dt2 \dfrac{d\theta (t)}{dt} \dfrac{d^2\theta (t)}{dt^2} = -2 \dfrac{g}{\ell}\theta (t) 2 \dfrac{d\theta (t)}{dt}
2dθ(t)d2θ(t)dt2=−2gℓθ(t)2dθ(t)2 d\theta (t) \dfrac{d^2\theta (t)}{dt^2} = -2 \dfrac{g}{\ell}\theta (t) 2 d\theta (t)
2dθ(t)d2θ(t)dt2=d(dθdt)22 d\theta (t) \dfrac{d^2\theta (t)}{dt^2} = d \left( \dfrac{d\theta}{dt}\right)^2

Je ne sais pas trop comment…

+0 -0

Euh… Je ne veux pas te faire peur mais tu m’inquiètes un peu là. Pour le document que tu as trouvé, c’est une manière de faire un peu lourdingue ici vu la simplicité de l’équation mais qui peut rendre service dans certains cas. L’idée est de faire apparaître l’énergie cinétique en gros. Tu as des forces à gauche, on les multiplie par θ˙\dot\theta pour avoir la puissance dégagée par leur travail qui est égale à la variation d’énergie cinétique. Ça c’est le côté physique du truc, mais mathétiquement on peut l’appliquer bêtement. Pour te convaincre que ça marche, tu sais normalement que d(f2)=2fdf\mathrm d(f^2)=2f\mathrm d f. Remplace ff par dθ\mathrm d\theta et voilà.

Bon sinon, j’avoue que dans cette instance je préfère largement une approche plus mathématique parce que clairement plus élégante en terme de calcul et plus facilement généralisable.

Si tu as une équation homogène du second ordre à coefficients constants af¨+bf˙+cf=0a\ddot f+b\dot f + cf = 0, un truc qui saute aux yeux directement est qu’en prenant ff une fonction propre de l’opération de dérivation, on va trouver facilement une solution. Essayons de voir ce que ça donne. La fonction propre de l’opération de dérivation par excellence et définition est l’exponentielle, donc prenons f(t)=exp⁡(λt)f(t)=\exp(\lambda t). En injectant dans l’équation, on trouve (aλ2+bλ+c)f=0(a\lambda^2+b\lambda+c)f = 0. On voit apparaître le polynôme caractéristique dont les racines sont λ±=−b±b2−4ac2a\lambda_\pm = \dfrac{-b\pm\sqrt{b^2-4ac}}{2a}.

Si elles sont distinctes, on a fini puisqu’on sait que l’espace des solutions est de dimension 2 et qu’on a trouvé nos deux fonctions de base t↦exp⁡(λ±t)t\mapsto\exp(\lambda_\pm t) pour le générer. Si elles ne sont pas distinctes, on peut remarquer que t↦texp⁡(λ±t)t\mapsto t\exp(\lambda_\pm t) est aussi solution et formera la deuxième fonction de base pour générer l’espace des solutions.

Enfin, si λ±\lambda_\pm est complexe, comme c’est le cas pour notre exemple, on remarque qu’elles sont aussi conjuguées. La solution va donc pouvoir, comme tu l’as dit, s’écrire facilement sous forme de cosinus et sinus de la partie imaginaire, et comme souligné par Vael précédemment, le coefficient b/(2a)b/(2a) (la partie réelle) donne l’amortissement/taux de croissance de la solution, ici 00.

+1 -0
Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte