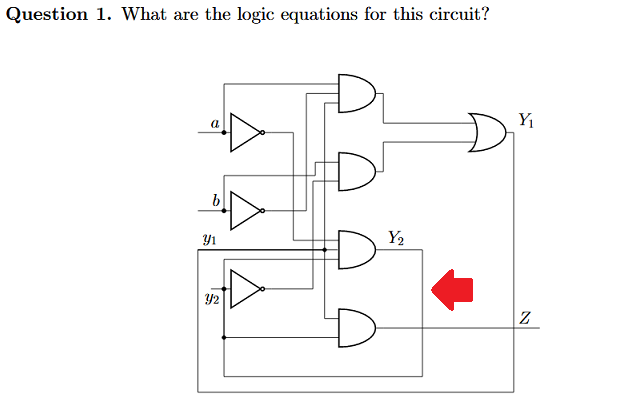
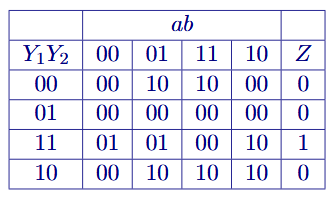
Dans la vraie vie, une porte logique a un temps de propagation, de l’ordre de la nanoseconde pour une porte CMOS par exemple. En l’absence de rétro-action, donc dans un circuit dit combinatoire, on s’en fout car on s’intéresse uniquement au régime permanent et non pas au régime transitoire. Mais quand tu introduis de la rétro-action, donc dans un circuit dit séquentiel, tu ne peux comprendre correctement ce qui se passe qu’en introduisant le paramètre temporel.
On a bien y2(t) = Y2(t) à tout instant comme tu l’as dit, vu que c’est le même noeud, mais on a aussi Y2(t) = a!(t - Tp) . y1(t - Tp) . y2(t - Tp) avec Tp le temps de propagation de la porte qui sort Y2. Ce n’est pas contradictoire.
En réalité, écrire des équations logiques sans paramètre temporel dans un circuit séquentiel n’a pas réellement de sens ; ce qu’on fait en général par convention, pour décrire de manière simple le comportement d’un tel circuit, c’est exprimer ses sorties en fonction de ses entrées à l’état "actuel" et de ses entrées à l’état "précédent", chaque état étant l’instant précis entre la production de la nouvelle sortie et la modification des entrées par rétro-action. Ou, quand on a un signal d’horloge, les états correspondent aux "ticks" de l’horloge.
Donc ici les équations données en solution sont valides, mais elles sont schématiques, elles permettent de donner une idée du comportement du circuit mais ne doivent pas être prises au pied de la lettre, il faut être conscient de ce qui est non-dit par ces équations (la présence de rétro-actions, le paramètre temporel et le temps de propagation) pour comprendre le comportement réel du circuit.
Pour donner un autre exemple, ici http://hyperphysics.phy-astr.gsu.edu/hbase/Electronic/nandlatch.html tu as le schéma d’un circuit NAND Latch, ce sont deux portes NAND tête-bêche qui permettent de garder un bit en mémoire. Le bit est gardé en mémoire car il tourne en boucle dans les portes NAND qui le régénèrent continuellement. Sur un tel circuit, tu peux écrire une équation si tu veux pour les états instables (set et reset), mais ça a beaucoup moins de sens pour l’état stable, vu que dans ce cas la sortie ne dépend pas des entrées mais de ce qui s’est passé avant (et ça peut être 1 seconde avant ou 1 heure, ça ne dépend pas du circuit mais de comment il a été utilisé). On le décrit donc par une table de vérité. Et là encore ce n’est pas une table de vérité au sens strict du terme, vu que "no change" n’est pas une valeur logique. Mais le but est simplement que tout le monde comprenne ce que fait le circuit.
Quand tu vas plus loin, tu te rends compte d’autres phénomènes, par exemple dans les portes CMOS on utilise des transistors P et N, qui ont un comportement légèrement asymétrique en réalité. Ce qui peut donner lieu à des comportements de circuits que tu n’aurais pas pu prévoir sans prendre ça en compte. Tu peux également avoir des comportements différents selon la technologie utilisée, par exemple si tu laisses une entrée dans le vide (en n’appliquant ni 0 ni 1). Bref, l’électronique logique n’est qu’une façon de schématiser les choses dans des configurations pas trop tordues, mais il faut être conscient que ce n’est qu’un schéma, une simplification de la réalité des lois physiques régissant les composants électroniques. 
Donc pour revenir à ta question exacte, ce n’est pas faux de dire que Y2 = y2, même si c’est imprécis, en tous cas ce n’est pas plus faux que de dire que Y2 = a! . y1 . y2 ; mais ce n’est pas ce qui est attendu.
C’est plus clair ?