Bonjour,
J’essaye de coder une simulation de l’Aiguille de Buffon Où l’on lance des aiguilles sur un plancher. Selon la loi des grands nombre la fréquence des aiguilles tombant entre deux lattes de plancher divisé par le nombre de lancer total est censé tendre vers 2/Pi
Seulement dans ma simulation , et ce même jusqu’à 10000 aiguilles, la valeur de Pi semble converger vers 2,7 .. o_O
J’ai essayé de modifier le nombre de planches, la taille des aiguilles mais rien n’y fait.
Voilà mon code:
from tkinter import *
from random import *
from math import *
root = Tk()
root.title('Aiguille de Buffon')
can = Canvas(root,width=1000,height=1000,bd=3)
def verifierIntersection(x1aig,y1aig,x2aig,y2aig,x1seg,y1seg,x2seg,y2seg,dessiner):
#On cherche les équations paramétriques des droites engandrées par les vecteurs
#aiguille
xaig = x1aig
yaig = y1aig
xvectaig = x2aig-x1aig
yvectaig= y2aig - y1aig
# On note le paramètre t
#autresegment
xseg = x1seg
yseg = y1seg
xvectseg = x2seg - x1seg
yvectseg = y2seg - y1seg
# On note le paramètre b
# Si le déterminant est non nul:
if (xvectaig*yvectseg-xvectseg*yvectaig != 0):
# On cherche les paramètres t et b codant le point d'intersection des droites
b = -(-xvectaig*yaig+xvectaig*yseg+yvectaig*xaig-yvectaig*xseg)/(xvectaig*yvectseg-yvectaig*xvectseg)
t = -(xaig*yvectseg-xseg*yvectseg-xvectseg*yaig+xvectseg*yseg)/(xvectaig*yvectseg-yvectaig*xvectseg)
if (0 <= b and 1>=b and 0 <= t and 1>=t):
#L'intersection est sur les deux segments
if dessiner == "oui":
xint = xaig + t*xvectaig
yint = yaig + t*yvectaig
can.create_oval(xint,yint,xint+4,yint+4,fill="red")
return True
else:
return False
else:
return False
def afficherPlancher():
can.create_line(200,300,800,300)
can.create_line(200,400,800,400)
can.create_line(200,500,800,500)
can.create_line(200,600,800,600)
can.create_line(200,700,800,700)
def afficherBords():
can.create_line(200,200,800,200)
can.create_line(200,200,200,800)
can.create_line(800,800,800,200)
can.create_line(800,800,200,800)
def chuteAiguille():
#Vérifie si l'aiguille sort du cadre
incorrect = True
while incorrect == True:
# On part d'un vecteur de norme 200
# le vecteur vérifie alors sqrt(x^2+y^2) = 200
# Les x et y vérifiant cette conditions forment l'équation d'un cercle de rxaigon 200.
# On isole un des paramètres pour trouver l'autre et voilà qu'on a généré les vecteurs aléatoirements
x3 = randrange(-100,101,1)
#change aléatoirement la coordonées y en négative ou positive
pos = randrange(0,2,1)
if pos == 0:
y3 = sqrt(10000-(x3**2))
else:
y3 = -sqrt(10000-(x3**2))
# Il ne reste plus qu'à générer des points aléatoirement qui seront l'origine de ces vecteurs.
# Une mauvaise restriction limite la probabilité de tomber dans les coins, ce qui empêche l'expérience
x1 = randrange(200,800,1)
y1 = randrange(200,800,1)
#Coordonnées du point d'arrivée
x2 = x1 + x3
y2 = y1 + y3
#Il faut vérifier si l'aiguille ne sorte pas du cadre
if verifierIntersection(x1, y1, x2, y2, 200, 200, 800, 200,"non") == False and verifierIntersection(x1, y1, x2, y2, 200, 200, 200, 800,"non") == False and verifierIntersection(x1, y1, x2, y2, 800, 800, 800, 200,"non") == False and verifierIntersection(x1, y1, x2, y2, 800, 800, 200, 800,"non") == False:
incorrect = False
can.create_line(x1,y1,x2,y2,fill="blue")
if verifierIntersection(x1,y1,x2,y2,200,300,800,300,"oui") == True or verifierIntersection(x1,y1,x2,y2,200,400,800,400,"oui") == True or verifierIntersection(x1,y1,x2,y2,200,500,800,500,"oui") == True or verifierIntersection(x1,y1,x2,y2,200,600,800,600,"oui") == True or verifierIntersection(x1,y1,x2,y2,200,700,800,700,"oui") == True:
return True
else:
return False
can.pack()
afficherPlancher()
afficherBords()
lancers = 0
collisions = 0
for i in range(10):
lancers = i
if chuteAiguille() == True:
collisions += 1
print(lancers+1, collisions)
can.create_text(400,100,text="PI = " + str((lancers/collisions)*2),width=700,font=("Arial",20))
mainloop()
Et voilà une petite image:
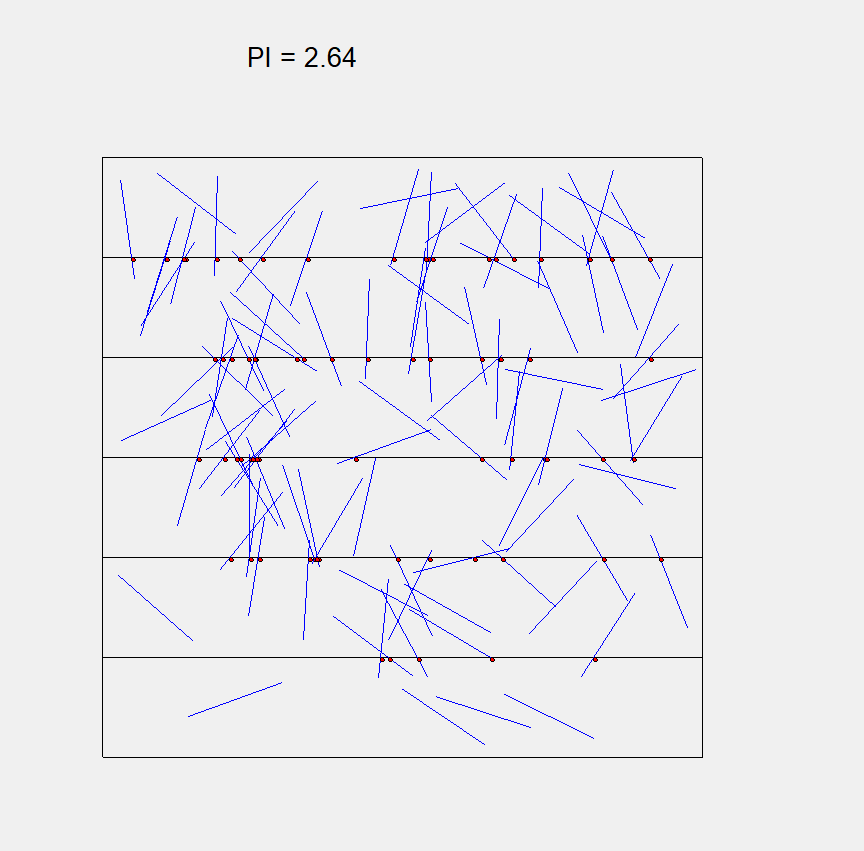
Si quelqu’un pourrait m’orienter vers une solution ? Merci d’avance
+0
-0


