Angle entre un point et l'axe des ordonnées

Bon jour à toutes et à tous,

pour un projet de robotique, j'aimerais calculer l'angle (en degré si possible) entre un point (dont je connais les coordonnées) et l'axes des ordonnées. J'ai bien une piste mais je ne suis pas sûr :

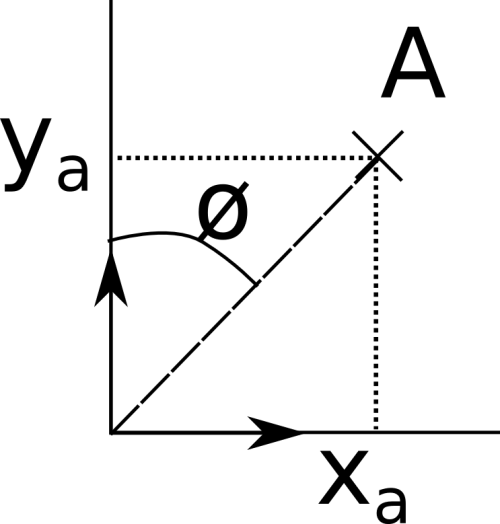
Dans le repère (O,I,J), considèrons un point A(xa, xb). Pour calculer l'angle O,ya,A, nous connaissons : la longueur du côté adjacent à l'angle (ya), et la longueur du côté opposé à l'angle (xa)

Donc si je ne me trompe pas, O,ya,A = Tan^-1(Opposé / Adjacent) = Tan^-1(xa/ya) ?

Merci d'avance

Merci de ta réponse

Avec quel logiciel as-tu fais ton schéma ? Car j'aurais bien voulu en faire un, mais je n'ai que Paint en logiciel de dessin 2D

Et par rapport aux limites de la fonction, comment pourrais-je obtenir un résultat allant de 0 à 360 (ou de 0 à 2 pi) ?

Car je voudrais l'utiliser pour un gestion de joystick pour diriger un robot, et il me faudrais l'angle pour la direction.

Avec quel logiciel as-tu fais ton schéma ? Car j'aurais bien voulu en faire un, mais je n'ai que Paint en logiciel de dessin 2D

J'ai utilisé Inkscape, mais c'est parce que c'est celui que je connais le mieux. Je suis sur que Paint/Paint.net permet de faire un truc vite-fait.

Déjà, je vais parler en radian, car c'est la pratique habituelle pour les fonctions trigo.. Tu veux donc un résultat entre $-\pi$ et $\pi$ (les fonctions renvoient des valeurs négatives, donc il faudra peut-être convertir après si tu veux un résultat entre 0 et $2\pi$). La fonction $\tan^{-1}$ donne des résultats entre $-\pi/2$ et $\pi/2$. Problème : pour les valeurs négatives, tu ne sais pas si c'est $x_a$ ou $y_a$ qui est négatif. Une solution (surement pas la seule, ni la meilleur ) est d'ajouter d'autres équations.

Voilà ce que je te propose : pour chacun des quatre cas :

• $x_a>0$, $y_a>0$
• $x_a>0$, $y_a<0$
• $x_a<0$, $y_a>0$
• $x_a<0$, $y_a<0$

, tu écris si les valeurs de $\tan^{-1}$ sont positives ou négatives. Tu vas ainsi « découper » ton espace en quatre blocs, et pouvoir calculer l'angle à l'aide de ces trois conditions (valeur de $\tan^{-1}$, signe de $x_a$, signe de $y_a$) et lever l’ambiguïté.

Un peu de trigo. n'a jamais tué personne !

P.S. : Fais des dessins.

Le plus simple pour les dessins rapides comme celui-là, c'est Geogebra. C'est un logiciel libre de géométrie dynamique, que je trouve pas top mal fait pour des usages élémentaires.

Pour les angles qui ne sont pas entre 0 et pi/2, la fonction réciproque de tangente ne pourra pas t'aider. Elle te donnera un résultat entre 0 et pi/2. À toi ensuite de retrouver le bon angle, en fonction des signes des composantes x et y de ton vecteur.

P.-S. Désolé pour la mise en forme, je rédige depuis une tablette, c'est pas tip top pour écrire du LaTeX. P.-P.-S OK over grilled, et le message de Gabbro est bien plus complet que le mien.

le message de Gabbro est bien plus complet que le mien.

Mais moins malin.

De un, Geogebra est effectivement très bien pour ça, de deux, poas besoin de s’embêter avec deux fonctions trigo quand on connait le signe de x et y.

J'édite…

Je tiens à préciser que je ne suis qu'en première S, que nous n'avons pas encore abordé la trigo, et que l'année dernière, nous n'en avons pas fait faute de temps… Donc les seules notions que j'ai dans ce domaine, ce sont mes vagues souvenir de 3ème.

Je voudrais pas être le premier O.o

J'ai vaguement compris ce que vous avez dit… Il faudrait donc que je calcul tan^-1, comme prévu, puis que je regarde les signes de mes deux coordonnées pour trouver dans quel quart du repère mon point se trouve ?

C'est ça. Le point délicat, ce sera de déterminé par rapport à quel axe tu mesure ton angle, puis d'ajouter ou retirer le bon nombre de $\pi/2$. N'hésite pas à vérifier, en fixant quelques valeurs de (x,y) (dans chaque quart), que tu obtiens bien le bon angle. Pour rappel, les valeurs remarquable du sinus et cosinus sont disponibles sur ce shémas. La lecture est la suivante : pour un angle de $\pi/6$, tu trouve un cosinus de $\sqrt{3}/2$ et un sinus de 1/2, donc une tangente de $1/\sqrt{3}$. Prends garde, ton angle n'est pas orienté pareil (sens différent : ton angle croisse « vers le bas » (sens anti-trigonométrique), axe de base différent (celui des y plutôt que celui des x)).

Il n'y a pas besoin de notions très approfondi, mais d'une rigueur implacable.

Pour que ça marche, il faudrait changer de sens ?