Dans la vie de tous les jours, on a affaire aux nombres. Et les mathématiciens, évidemment, utilisent les nombres quotidiennement : ils jouent avec, essayent de comprendre leurs propriétés et comparent les différentes « sortes » de nombres qui existent.
Une question que les mathématiciens se sont posés (et à laquelle ils ont répondu) il y a environ 150 ans, est de savoir combien il y a de nombres. Il est assez clair pour tout le monde qu’il y en a un nombre infini. Mais peut-on donner un sens plus précis à cette notion ? En particulier, tous les ensembles de nombres contiennent-ils le même… nombre d’éléments ? Y a-t-il autant de nombres entiers positifs que de fractions ? Et que d’irrationnels ?
C’est à cette question que je vous propose de répondre dans ce mini-tutoriel. Nous allons mener des raisonnements parfois un peu compliqués, mais vous verrez que, si vous ne vous précipitez pas, vous pourrez tout comprendre. Les raisonnements mathématiques ne seront jamais très longs, et feront appel à des notions assez intuitives. Ce tutoriel est auto-contenu, c’est à dire que toutes les notions qui nous seront utiles seront présentées en amont. Cela a deux conséquences : la première est qu’il n’y a aucun prérequis nécessaire à la lecture, si ce n’est de connaître les notions de nombres entiers, de fractions et les autres choses élémentaires en rapport avec les nombres ; la deuxième est que les outils présentés ne le sont que dans le cadre restreint qui nous est utile, et seul le strict nécessaire est expliqué pour pouvoir aller au bout du tutoriel. Pour autant, nous allons démontrer des résultats à vous faire hérisser les cheveux sur la tête : nous parlerons de choses extrêmement profondes, et nous verrons notamment qu’il y a des infinis de différentes tailles.
Nous allons, dans ce tutoriel, parler de produits cartésiens, d’ensembles dénombrables, indénombrables et de bijections. En route. 
- Ensembles et ensembles de nombres
- Suites, fonctions et bijections
- Cardinaux et ensembles dénombrables
- Vers l'infini, et au-délà
Ensembles et ensembles de nombres
Avant d’entrer dans le vif du sujet, nous allons avoir besoin de plusieurs notions. Dans cette première partie, je vais surtout vous parler des ensembles, plus particulièrement des ensembles de nombres puisque ce sont eux qui vont nous intéresser. Ensuite, je vous parlerai d’une opération que l’on peut réaliser sur les ensembles : le produit cartésien.
Notions générales sur les ensembles
Quelques définitions et premières notions
D’abord, qu’est-ce qu’un ensemble en mathématiques ? Là, je ne vais pas répondre. Je vous dirai simplement que les ensembles désignent des « paquets » d’objets. Par exemple, si en bas de chez vous il y a des voitures stationnées, elles constituent un ensemble, dans lequel chaque élément est une voiture.
Lorsque l’on travaille avec des ensembles quelconques, on les note souvent avec les lettres E, F, etc. (lettres majuscules). Les ensembles sont de toutes sortes : ensembles de voitures du parking, ensemble des lettres dans votre boîte aux lettre, ensemble des particules de l’univers, ensemble des lettres de l’alphabet et des mots d’une langue (l’étude de ces ensembles d’un point de vue mathématique constitue la théorie des langages). Il y a aussi des ensembles infinis, par exemple l’ensemble des nombres positifs ou l’ensemble des couleurs de l’arc-en-ciel, ou encore l’ensemble des points sur une droite.
Considérons par exemple l’ensemble fini contenant les couleurs bleu, rouge, vert. Pour désigner cet ensemble, on note {bleu, rouge vert}.
Hey ! Minute, pourquoi tu as noté les valeurs entre accolades ?
Il s’agit d’une convention d’écriture : en maths, les éléments contenus dans un ensemble sont notés entre accolades.
Comme je vous l’ai dit, les ensembles contiennent des objets (qui peuvent être des voitures, des nombres, des points du plan mathématique, etc.). Si $E$ est un ensemble et $x$ désigne un élément qui est dans $E$, on note $x\in E$, qui se lit « $x$ appartient à $E$ ». Par exemple, bleu$\in${bleu, rouge, vert} mais jaune$\notin${bleu, rouge, vert} (lire « jaune n’appartient pas à {bleu, rouge, vert} »).
Une notion importante pour travailler avec les ensembles est la notion d’inclusion. On dit qu’un ensemble $E$ est inclus dans un ensemble $F$ si tous les éléments de $E$ appartiennent à $F$. Autrement dit, pour tout $x\in E$, on a en fait $x\in F$. Par exemple, l’ensemble {vert, bleu} est inclus dans l’ensemble {rouge, vert, bleu}, mais pas l’ensemble {vert, jaune}, ni l’ensemble {jaune}. Si $E$ est inclus dans $F$, on note $E\subset F$.
Ces quelques paragraphes sont un peu abstraits car je n’ai parlé que d’ensembles généraux. Avec les ensembles de nombres, nous allons rencontrer davantage d’exemples, ce qui devrait vous éclairer un peu.
Produit cartésien d’ensembles
Je vais ici travailler directement sur un exemple, avant de donner la définition plus générale de ce qu’est un produit cartésien. Considérons un ensemble V de marques de voitures et C un ensemble de couleurs. Pour fixer les idées, supposons V = {Mercedes, Jaguar, Porsche, Maserati} (ben quoi, quitte à faire des maths, autant se faire rêver un peu  ) et C = {rouge, vert, bleu}. On dispose de deux ensembles distincts, contenant des objets de natures différentes (l’un contient des voitures, l’autre des couleurs). On peut réaliser une opération, appelée le produit cartésien de V et C, qui donne un nouvel ensemble. Ce nouvel ensemble contiendra tous les couples possibles voiture-couleur. On notera ces couples entre parenthèses : (voiture, couleur). Ainsi, (Maserati, bleu) sera un élément de notre nouvel ensemble.
) et C = {rouge, vert, bleu}. On dispose de deux ensembles distincts, contenant des objets de natures différentes (l’un contient des voitures, l’autre des couleurs). On peut réaliser une opération, appelée le produit cartésien de V et C, qui donne un nouvel ensemble. Ce nouvel ensemble contiendra tous les couples possibles voiture-couleur. On notera ces couples entre parenthèses : (voiture, couleur). Ainsi, (Maserati, bleu) sera un élément de notre nouvel ensemble.
Ce nouvel ensemble est noté V×C (lire « V croix C »). Pouvez-vous lister tous les éléments qu’il contient ? Je vous rappelle que dans V×C, chaque élément est un couple, c’est à dire que V×C est un ensemble de paires (voiture, couleur). La réponse est cachée ci-dessous.
V×C = {(Mercedes, rouge), (Mercedes, vert), (Mercedes, bleu), (Jaguar, rouge), (Jaguar, vert), (Jaguar, bleu), (Porsche, rouge), (Porsche, vert), (Porsche, bleu), (Maserati, rouge), (Maserati, vert), (Maserati, bleu)}
C’est un peu compliqué à écrire (surtout au clavier), mais il n’y a rien de sorcier une fois qu’on a compris l’idée.
S’il y a des amateurs de programmation parmi vous, je vous propose un petit exercice. Essayez d’écrire un script dans votre langage de programmation préféré qui, étant donnés deux ensembles E et F, dresse la liste des éléments de E×F.
Ici, nous avons travaillé avec deux ensembles finis. Une bonne question est de savoir, étant donnés deux ensembles E et F, combien l’ensemble E×F contient d’éléments. Cette question n’est pas extrêmement difficile, mais elle n’est pas non plus d’objet de ce tutoriel donc je ne vais pas en parler. Google vous aidera à y répondre si cette question vous intéresse.
Nous, on va faire des choses beaucoup plus tordues : nous allons faire des produis cartésiens d’ensembles infinis. Mais pour cela, il faut attendre la suite de ce tutoriel. Avant cela, essayons de prolonger l’exemple ci-dessus. Nous avons notre ensemble V de voiture et notre ensemble C de couleurs. Nous avons construit l’ensemble V×C des couples (voiture, couleur). Imaginons maintenant que nous ayons un ensemble P de prix. Pour faire simple, disons que P = {10, 15} (ben quoi, une Jaguar à 10 €, c’est pas mal, non ?). Essayez de construire le produit cartésien V×P (couples (voiture, prix)) et même le produit C×P (ensemble des couples (couleur, prix) — ça n’a pas tellement de sens en pratique, mais ça existe quand même).
On peut faire le produit cartésien de deux ensembles… et pourquoi pas de trois ensembles ? Ainsi, essayez de déterminer le produit cartésien de V, C, P. Ce sera un ensemble de triplets de valeurs, cf. le résultat masqué ci-dessous.
V×C×P = {(Mercedes, rouge, 10), (Mercedes, rouge, 15), (Mercedes, bleu, 10), (Mercedes, bleu, 15), (Mercedes, vert, 10), (Mercedes, vert, 15), , (Jaguar, rouge, 10), (Jaguar, rouge, 15), (Jaguar, bleu, 10), (Jaguar, bleu, 15), (Jaguar, vert, 10), (Jaguar, vert, 15), (Porsche, rouge, 10), (Porsche, rouge, 15), (Porsche, bleu, 10), (Porsche, bleu, 15), (Porsche, vert, 10), (Porsche, vert, 15), (Maserati, rouge, 10), (Maserati, rouge, 15), (Maserati, bleu, 10), (Maserati, bleu, 15), (Maserati, vert, 10), (Maserati, vert, 15)}
Là, ce n’est vraiment pas facile à écrire. Mais bon, on y arrive quand même.
On peut donc faire des produits cartésiens de deux et trois ensembles. Je pense que vous aurez compris que l’on peut continuer ainsi et faire des produits cartésiens d’un nombre quelconque d’ensembles. On peut également faire un produit cartésien d’un ensemble avec lui-même. Par exemple, déterminez l’ensemble V×V, et l’ensemble P×P×P. Combien contiennent-ils d’éléments ?
Note aux programmeurs — C’est le moment de généraliser le script que vous avez écrit plus haut pour qu’il soit capable, étant donné des ensembles en nombre quelconque (fini, bien sûr), de donner la liste de leur produit cartésien
J’ai pris ici des exemples avec des ensembles finis pour pouvoir illustrer facilement la notion. Mais cela fonctionne exactement de la même manière pour les ensembles infinis. Dans la suite de cette section, nous déterminerons des produits cartésiens d’ensembles infinis.
Avant de passer à la suite, petite note historique. Le terme « produit cartésien » a été choisi en hommage à René Descartes, un éminent mathématicien des XVIe et XVIIe siècles. Remarquez que c’est le même homme qui a théorisé la notion philosophique du cogito (« Je pense, je suis »).
Ensembles de nombres
Nombres entiers naturels
Avant de parler de choses plus compliquées, parlons des ensembles de nombres. Dans ce tutoriel, nous allons beaucoup parler des nombres. Nous allons même essayer de les compter. Commençons par le plus facile : les nombres entiers naturels. Ceux-là, vous les connaissez : 0, 1, 2, 3, 4, etc., sont des nombres entiers positifs. De façon intuitive, les nombres entiers naturels sont les nombres positifs (y compris zéro) qui n’ont pas de virgule. On note $\mathbb N$ cet ensemble, et on a donc $\mathbb N = \{0, 1, 2, 3, …\}$. Souvenez-vous que pour désigner l’appartenance à un ensemble, on utilise le symbole $\in$. Ainsi, comme 4 est un nombre entier naturel, on note $4\in\mathbb N$ et $-2,5\notin\mathbb N$, car 2,5 n’est pas un entier naturel.
Si je veux considérer l’ensemble des nombres entiers naturels pairs, je le note $\{2n, n\in\mathbb N\}$ : c’est l’ensemble des nombres qui s’écrivent comme le double d’un nombre entier. Remarquez qu’ici, je n’ai pas défini l’ensemble en faisant la liste de ses éléments ; j’ai donné une propriété qui caractérise les éléments de mon ensemble. On fait cela très souvent en mathématiques, parce que l’on manipule des ensembles trop grands pour lister leurs éléments. Prenons un autre exemple. Je veux décrire l’ensemble des nombres entiers négatifs. Naïvement, c’est l’ensemble {…, -4, -3, -2, -1, 0}. Mais cette notation n’est pas satisfaisante mathématiquement. De manière rigoureuse, l’ensemble des entiers négatifs est l’ensemble des opposés des entiers naturels. Une manière de le décrire est la suivante : $\{-n, n\in\mathbb N\}$.
Si vous êtes vraiment attentif, vous aurez remarqué que j’aurais dû décrire l’ensemble des entiers naturels à l’aide d’une propriété caractéristique. Je ne l’ai pas fait, car dans le cadre de ce tutoriel on considérera que l’ensemble des entiers naturels est défini sans ambiguïté comme je l’ai fait plus haut. Mais sachez qu’il est possible de construire $\mathbb N$ de manière rigoureuse ; simplement, cela sort largement de notre cadre.
Une dernière petite remarque annexe. Si, lorsque je définis un ensemble à l’aide d’une propriété manifestement fausse, alors cet ensemble est vide. Avant de donner un exemple, on appelle ensemble vide l’ensemble qui ne contient aucun élément. Autrement dit, l’ensemble vide est l’ensemble {}. Cette notation est un peu désagréable, c’est pourquoi on a introduit un symbole spécial pour désigner l’ensemble vide : le symbole $\varnothing$. Par exemple, l’ensemble des entiers naturels strictement négatifs est vide. En symboles, $\{n\in\mathbb N, n<0\} = \varnothing$.
Nombres entiers relatifs
Les nombres entiers relatifs sont les nombres entiers positifs (c’est à dire les entiers naturels) et les nombres entiers négatifs. On note $\mathbb Z$ cet ensemble, et donc $\mathbb Z = \{…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …\}$. Remarquez que les entiers naturels font partie des entiers relatifs. Autrement dit, tout élément de $\mathbb N$ est également un élément de $\mathbb Z$. Cela signifie que $\mathbb N$ est inclus dans $\mathbb Z$, on note donc $\mathbb N \subset\mathbb Z$.
Et là, je vous fais une première remarque. On a l’impression que $\mathbb N$ est « plus petit » que $\mathbb Z$, ce qui est vrai en un sens car $\mathbb N\subset\mathbb Z$. Pourtant, nous verrons plus loin qu’en fait, il n’en est rien : ces deux ensembles contiennent autant d’éléments. Évidemment, ils sont tous les deux infinis, donc il faudra d’abord définir précisément ce que signifie « avoir le même nombre d’éléments » dans le cadre des ensembles infinis.
C’est l’occasion de faire une remarque de terminologie assez centrale en sciences et en mathématiques plus particulièrement : il faut prendre garde au sens que l’on donne aux mots. Lorsque j’affirme que $\mathbb N$ est « plus petit » que $\mathbb Z$, c’est vrai en un certain sens : après tout, $\mathbb N\subset \mathbb Z$. Mais pourtant, comme je le disais, il est possible — et nous allons le faire — de démontrer qu’ils sont de même cardinal. Ainsi, il est vrai que $\mathbb N$ est plus petit que $\mathbb Z$ au sens de l’inclusion, mais c’est faux au sens des cardinaux. Sachez d’ailleurs que c’est un phénomène très courant en mathématiques : étant donné deux ensembles E et F, l’un peut être plus petit que l’autre en un certain sens, mais plus grand en un autre sens. En fait, c’est un phénomène tellement courant que cela a été formalisé par la notion de relation d’ordre, qui explique comment on peut comparer deux ensembles.
Nombres rationnels
Les nombres rationnels portent un nom bien compliqué. Mais en fait, les nombres rationnels sont simplement les fractions, c’est à dire les nombres qui s’écrivent comme le quotient de deux nombres entiers. Par exemple, $\frac13$, $\frac25$, $\frac{-10}{1564}$ sont des fractions. Mais les nombres entiers relatifs (et donc aussi les entiers naturels) sont également des fractions. De fait, le nombre -3, par exemple, peut s’écrire sous la forme $\frac{-3}{1}$. C’est donc une fraction. Zéro est également une fraction, car on peut l’écrire $\frac01$. Ainsi, l’ensemble des nombres relatifs est inclus dans l’ensemble des rationnels.
Pour ceux d’entre vous que le vocabulaire intéresse, le nombre au-dessus de la barre de fraction est appelé le numérateur ; celui qui est sous la barre est appelé le dénominateur. Mais rassurez-vous, je n’utiliserai pas ce vocabulaire par la suite, ce tutoriel étant déjà suffisamment dense.
L’objectif de ce tutoriel n’est pas de vous apprendre à calculer avec les fractions, pour faire cela, je vous redirige vers Google et vos cours de maths de collège.  Néanmoins, je vous rappelle, car ça sera important pour la suite, qu’un même nombre rationnel admet de nombreuses écritures. En effet, par exemple, on a toujours $\frac12 = \frac24 = \frac36 = \frac{5}{10}$. Il en est de même pour tous les nombres rationnels : multiplier en haut et en bas par un même nombre entier (non nul) conserve la valeur de la fraction. Ainsi, chaque nombre rationnel admet un nombre infini de représentants, qui sont en fait tous égaux au même nombre. Il faudra prendre en compte ce phénomène lorsque nous voudrons compter les nombres rationnels. Pour éviter cette difficulté, nous allons donc travailler avec l’ensemble des nombres rationnels dits irréductibles.
Néanmoins, je vous rappelle, car ça sera important pour la suite, qu’un même nombre rationnel admet de nombreuses écritures. En effet, par exemple, on a toujours $\frac12 = \frac24 = \frac36 = \frac{5}{10}$. Il en est de même pour tous les nombres rationnels : multiplier en haut et en bas par un même nombre entier (non nul) conserve la valeur de la fraction. Ainsi, chaque nombre rationnel admet un nombre infini de représentants, qui sont en fait tous égaux au même nombre. Il faudra prendre en compte ce phénomène lorsque nous voudrons compter les nombres rationnels. Pour éviter cette difficulté, nous allons donc travailler avec l’ensemble des nombres rationnels dits irréductibles.
Pour finir, il faut que vous sachiez que l’ensemble des nombres rationnels irréductibles est noté $\mathbb Q$. Rappelez-vous également que lorsque l’on veut donner la définition d’un ensemble, on l’écrit entre accolades. Ainsi, une manière de définir $\mathbb Q$ est la suivante : $\mathbb Q = \{\frac{p}{q}, p\in\mathbb Z, q\in\mathbb N, q\not=0, p\wedge q = 1\}$. La notation $p\wedge q = 1$ spécifie que l’ensemble $\mathbb Q$ ne contient que des fractions irréductibles, donc qu’il ne contient qu’un seul « exemplaire » de chaque rationnel. Ainsi, lorsque nous dénombrerons $\mathbb Q$, nous compterons exactement le nombre de rationnels distincts, en ne comptant pas les doublons plusieurs fois. Vous observez donc que $\mathbb Q$ est l’ensemble des éléments « $p$ sur $q$ avec $p$ entier relatif et $q$ entier naturel non nul »… Pourquoi demander que $q$ soit non nul ? Eh bien, simplement parce que l’on ne divise pas par zéro. On ne veut donc pas de zéro en bas de la fraction. Bien sûr, il y a de nombreuses manières de définir $\mathbb Q$, mais heureusement, elles sont toutes équivalentes. Mais celle que j’ai choisie permet de bien voir que l’on ne divise pas par zéro… Et en plus elle est bien pratique pour compter les éléments, comme vous le verrez plus tard.
Souvenez-vous que les entiers relatifs sont inclus dans les rationnels. Donc $\mathbb Z\subset\mathbb Q$. Et on a aussi $\mathbb N\subset\mathbb Z\subset\mathbb Q$.
Nombres irrationnels
Jusqu’à maintenant, nous avons parlé de nombres avec lesquels vous êtes vraisemblablement familiers : entiers, relatifs, fractions. Mais il y a des nombres que l’on ne peut pas écrire sous la forme de fractions. Le plus célèbre est probablement $\pi$, la fameuse constante qui permet de calculer le périmètre d’un cercle en connaissant son rayon. On pourrait écrire tout un tutoriel rien que pour parler du nombre pi. D’ailleurs, ça a été fait par nul autre que Cécric Villani, mathématicien médaillé Fields en 2010 pour ses travaux de recherche. Je n’ai pas lu ce livre, mais normalement il est accessible si vous êtes déjà un peu familier avec les maths.
Le nombre $\pi$ ne se laisse pas mettre sous forme de fraction. Autrement dit, les chiffres après sa virgule sont en nombre infini, et surtout il n’y a pas de cycle dans les chiffres après la virgule. C’est une caractéristique de ces nombres. On dit que ce sont des nombres irrationnels. $\pi$ est un nombre irrationnel célèbre, mais il est compliqué : les mathématiciens ignorent encore beaucoup de choses sur ce nombre. Je vous propose de parler d’un autre nombre irrationnel, un peu plus simple. Il s’agit du nombre $\sqrt 2$.
Je vous rappelle que $\sqrt 2$ est le nombre positif tel que, lorsqu’on l’élève au carré, on obtient 2. Ainsi, $\sqrt2\times\sqrt 2 = 2$. Eh bien, ce nombre ne peut pas être écrit comme le quotient de deux nombres entiers. Autrement dit, il est irrationnel. Je vous propose de démontrer cette propriété à l’aide d’un raisonnement par l’absurde.
Hop, hop ! Question ! C’est quoi un raisonnement par l’absurde ?
En mathématiques, lorsque l’on veut démontrer un résultat, il y a quelques règles. On utilise des arguments logiques et d’autres résultats préalablement démontrés, afin d’obtenir de nouvelles propriétés. Le raisonnement par l’absurde est une stratégie de démonstration. Elle consiste à supposer que le résultat que l’on cherche à obtenir est faux, et à essayer d’obtenir une contradiction. Si on obtient une contradiction, cela veut dire que lorsque l’on suppose le résultat faux, on peut démontrer des choses fausses… Donc le résultat est vrai.
Ainsi, nous allons supposer que $\sqrt 2$ est un nombre rationnel. Il existe $p$ un entier naturel et $q$ un entier relatif non nul tels que $\sqrt 2 = \frac pq$. On suppose en outre que $\frac pq$ est irréductible, c’est à dire que l’on a choisi la fraction la plus simple possible pour représenter $\sqrt 2$ (n’oubliez pas qu’il existe une infinité de représentations d’une même fraction). On sait que : $\sqrt 2^2 = 2$. Mais aussi, $\sqrt 2^2 = \left(\frac pq\right)^2 = \frac{p^2}{q^2}$. Donc $\frac{p^2}{q^2} = 2$. Donc, en multipliant par $q^2$ de part et d’autre, $p^2 = 2q^2$. Donc $p^2$ est un nombre pair, et donc $p$ est aussi un nombre pair.
En effet, lorsque le carré d’un nombre est pair, alors le nombre de départ est également pair. Par exemple, 36 est pair et 6 est pair, 64 est pair et 8 est pair, etc.
Comme $p$ est pair, on peut trouver un nombre entier, disons $r$, tel que $p = 2r$. Donc $p^2 = 4r^2$. Donc $2q^2 = 4r^2$. Donc $q^2 = 2r^2$. Donc $q$ est pair, donc on peut trouver un nombre entier $s$ tel que $q = 2s$. Donc $\frac pq = \frac{2r}{2s}$. Mais nous avions supposé que la fraction $\frac pq$ était la plus simple possible, et nous venons de démontrer qu’en fait, on peut encore la simplifier par 2. Ceci est contradictoire, donc il est impossible que $\sqrt 2$ soit un nombre rationnel !
Ainsi, nous avons trouvé un nombre qui ne peut pas s’écrire sous la forme d’une fraction. Ces nombres sont appelés, comme je le disais, des nombres irrationnels. Il n’y a pas de notation pour cet ensemble, qui est pourtant très important et assez compliqué. Je vous propose d’adopter la notation non standard $\mathbb V$ pour désigner l’ensemble des nombres irrationnels.
Attention, attention — Cette notation $\mathbb V$ pour désigner les irrationnels n’est pas standard, c’est à dire qu’elle sera interne à ce tutoriel. À ma connaissance, il n’existe pas de notation couramment utilisée, donc il faut bien en inventer une. J’ai choisi la lettre $\mathbb V$ car les lettres $\mathbb{R, S, T, U}$ sont habituellement utilisées pour d’autres choses… Et je ne souhaite pas changer les normes.
Pour votre curiosité, et si vous avez déjà fait un peu de maths, sachez que la constante $e$ est également irrationnelle.
De par leur nature, les nombres irrationnels sont plus difficiles à comprendre que les rationnels. Vous verrez que nous allons avoir du mal à les compter !
Nombres réels : la vraie grandeur
Venons-en au dernier ensemble de nombre dont je voulais vous parler : l’ensemble des nombres réels. C’est facile : c’est l’ensemble de tous les nombres que nous avons vus jusqu’à maintenant : entiers naturels, entiers relatifs, rationnels, et irrationnels (qui sont un peu à part). On a vu que $\mathbb N\subset\mathbb Z\subset\mathbb Q$. Par contre, l’ensemble des irrationnels est séparé. En particulier, $\mathbb Q$ n’est pas inclus dans $\mathbb V$. En fait, les nombres rationnels ne sont pas irrationnels et les nombres irrationnels ne sont pas rationnels — la terminologie est bien choisie. On dit que $\mathbb Q$ et $\mathbb V$ ne s’intersectent pas, parce qu’ils n’ont aucun élément en commun.
L’ensemble de tous les nombres, rationnels et irrationnels s’appelle l’ensemble des nombres réels et est noté $\mathbb R$.
Produits cartésiens d’ensembles de nombres
Si vous n’êtes pas à l’aise avec ce qui a été fait jusqu’à maintenant, faites une pause et relisez à tête reposée demain ou dans deux jours. Parce que ce que nous allons faire ici nécessite une bonne compréhension de ce qui précède, notamment la partie sur les produits cartésiens.
Nous avons vu comment faire des produits cartésiens d’ensembles, et nous avons vu les ensembles de nombres. Qu’est-ce qu’on va pouvoir faire maintenant ? Des produits cartésiens d’ensembles de nombres, évidemment. 
Un premier exemple : $\mathbb{N}\times\mathbb N$
Commençons gentiment avec l’ensemble $\mathbb N\times\mathbb N$ ; c’est l’ensemble des couples de nombres entiers : (0, 0), (0, 1), (1, 0), (1, 1), (1, 2), (2, 1), (2, 2), etc. Attention, l’ordre compte, donc (1, 2) et (2, 1) ne sont pas égaux. Formellement, le produit $\mathbb N\times\mathbb N$ admet la définition suivante : $\mathbb N\times\mathbb N = \{(m, n), n\in\mathbb N, m\in\mathbb N\}$. Un dessin sera sans nul doute plus parlant :
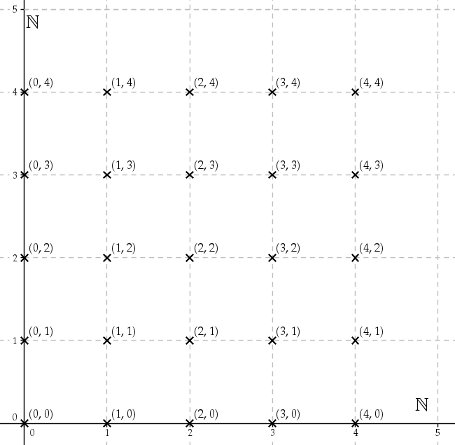
Et les nombres rationnels ?
Nous allons ici voir quelque chose qui va peut-être vous surprendre. Mais de toute façon, vous risquez d’être surpris plusieurs fois pendant ce tutoriel, alors autant vous préparer.  Vous allez voir que l’ensemble des nombres rationnels peut être réinterprété en terme de produit cartésien.
Vous allez voir que l’ensemble des nombres rationnels peut être réinterprété en terme de produit cartésien.
Vous souvenez-vous de la définition de l’ensemble $\mathbb Q$ que je vous avais donnée ? On avait vu que $\mathbb Q = \{\frac pq, p\in\mathbb Z, q\in\mathbb N, q\not=0, p\wedge q = 1\}$. Grâce aux produits cartésiens, on peut facilement donner une définition plus simple de cet ensemble. En fait, un nombre rationnel n’est rien d’autre que la donnée d’un nombre entier naturel et d’un nombre entier relatif (non nul). Autrement dit, $\mathbb Q$ est l’ensemble des couples (entier naturel, entier relatif non nul). Mais là, nous voyons un produit cartésien apparaître. Certes, me direz-vous, un rationnel s’écrit $\frac pq$, sous la forme d’une fraction. Mais dans le fond, ce n’est qu’une écriture et on pourrait très bien décider que les rationnels s’écrivent $(p, q)$. On aurait un peu changé la notation, mais la nature de ce qu’est l’ensemble $\mathbb Q$ serait restée la même. Ainsi donc, on peut dire que $\mathbb Q = \mathbb Z\times\mathbb N^*$. La notation $\mathbb N^*$ désigne simplement l’ensemble $\mathbb N$ duquel on a retiré zéro, c’est à dire $\mathbb N^* = \{1, 2, 3, 4, …\}$.
Mais alors, si $\mathbb Q$ est en fait un produit cartésien, pourquoi a-t-on changé de notation et adopté l’écriture avec les fractions ?
La réponse va sûrement vous surprendre : on le fait parce que c’est pratique. Lorsque l’on souhaite calculer avec des rationnels (additions, soustractions, produits), la présentation sous forme de fraction est plus facile à manipuler. En outre, la présentation $\frac pq$ nous incite à penser $\frac pq$ comme une division, ce qui est exactement l’objectif. Si l’on avait écrit $(p, q)$, on aurait également eu affaire à une division, mais ce n’est pas aussi confortable à manipuler.
Venons-en maintenant à deux autres notions requises avant de passer au vif du sujet : les suites et les fonctions.
Suites, fonctions et bijections
Nous avons (un peu) vu les ensembles, nous avons parlé des nombres et je vous ai expliqué ce qu’est un produit cartésien d’ensembles. Nous n’avons pas encore commencé à « compter les nombres », parce que nous n’avons pas encore tous les outils nécessaires : il nous faut encore parler de suites, de fonctions et de bijections. Comme nous allons utiliser toutes ces notions, je vais les passer en revue et vous en parler un peu. Nous allons faire pas mal de vocabulaire et ça n’est pas toujours très amusant, mais c’est nécessaire. Et je vous ai concocté des exemples que j’espère éclairants.
Notion de suite et de suite bijective
Les suites
Cette notion nous sera très utile par la suite (haha). En mathématiques, les suites sont des objets cruciaux. Ils interviennent dans absolument toutes les branches des mathématiques. Il n’est donc pas question ici de vous faire un cours sur les suites : je vais seulement introduire ce qui nous sera utile pour la suite, et vous verrez que seules les notions les plus élémentaires vont être traitées.
Si vous avez suivi, à l’école (au lycée, vraisemblablement — pour les lecteurs français en tout cas) des cours sur les suites, vous aurez peut-être l’impression que ce que je vous raconte n’a rien à voir. C’est parce que les suites, en mathématiques, sont des objets très généraux. Et dans les lycées, on parle essentiellement des suites numériques récurrentes, qui sont vraiment des suites très particulières.
En outre, désolé pour les puristes, mais je vais ici me contenter de définitions informelles.
Commençons par une définition. Une suite est un opérateur qui prend un nombre entier naturel et qui lui associe… une valeur. Mais une valeur peut être n’importe quoi : un nombre, un couple de nombres, et même, pourquoi pas, un ensemble. Dans ce tutoriel, ce sont les suites qui prennent des valeurs numériques qui nous intéresseront. On note souvent $u$ et $v$ les suites. Par exemple, on peut imaginer la suite qui, à tout entier naturel, associe son opposé. Ainsi, la suite prendra les valeurs suivantes :
| Variable | Valeur |
|---|---|
| 0 | 0 |
| 1 | -1 |
| 2 | -2 |
| 3 | -3 |
| … | … |
Notons $u$ la suite qui prend un nombre entier naturel et lui associe son opposé. Comme $u$ agit sur $\mathbb N$ et prend ses valeurs dans $\mathbb Z$, on note $u: \mathbb N\to\mathbb Z$. On utilise aussi la notation $(u_n)_{n\in\mathbb N}$ pour désigner la suite $u$. La notation $u_n$ désigne la valeur du nombre $u_n$. Par exemple, $u_{17} = -17$, dans l’exemple précédent. Une suite peut prendre des valeurs dans n’importe quel ensemble, pas forcément dans $\mathbb Z$.
De manière générale, si $E$ est un ensemble quelconque, et si $(u_n)_{n\in\mathbb N}$ est une suite à valeurs dans $E$, on note $u: \mathbb N\to E$. Néanmoins, attention : ce n’est pas parce que la suite prend ses valeurs dans $E$ que tous les éléments de $E$ correspondent à une valeur que prend la suite. Par exemple, soit $u:\mathbb N\to\mathbb Z$ la suite définie par $u_n = -2n$. Cette suite associe l’opposé du double d’un entier ; ses premières valeurs sont les suivantes :
| $n$ | $u_n$ |
|---|---|
| 0 | 0 |
| 1 | -1 |
| 2 | -4 |
| 3 | -6 |
| 4 | -8 |
Cette suite est à valeurs dans $\mathbb Z$, mais certains entiers relatifs ne correspondent à aucun indice $n$. Par exemple, il n’existe aucun entier naturel $n$ tel que $u_n = -7$. De même, aucun nombre positif n’est représenté par un indice de la suite.
Je rebondis pour faire un point de vocabulaire, même si j’éviterai de m’en servir par la suite. Si $n$ est un entier naturel, on dit que $n$ est un antécédent de $u_n$. Dans l’exemple précédent, 7 n’admet pas d’antécédent.
Ainsi, on peut considérer la suite $(v_n)_{n\in\mathbb N}$, qui à un nombre entier naturel $n$ associe le produit cartésien de tous les entiers plus petits que $n$. Autrement dit, $v_0 = 0$, $v_1 = (0, 1)$, $v_2 = (0, 1, 2)$, …, $v_n = (0, 1, 2, …, n-1, n)$. L’ensemble d’arrivée de cette suite est assez compliqué, je ne vais donc pas vous le donner. C’est très mal de faire cela : normalement, lorsque l’on définit une suite, il faut obligatoirement donner son ensemble d’arrivée. L’exemple que je viens de donner sera la seule entorse à ce principe.
Ce qu’il est important de retenir, c’est qu’une suite prend un nombre entier naturel et agit dessus. On dit que la suite suite admet une variable qui est un entier naturel, ou encore que la suite est indicée par les entiers naturels. Si vous êtes habitués à programmer, vous pourrez y voir une analogie avec une fonction dans votre langage de programmation favoris, qui prend un int en paramètre, et renvoie n’importe quel type de valeur ou d’objet.
Je terminerai cette partie en parlant d’une suite particulière : la suite qui à un entier naturel $n$ associe… l’entier $n$ lui-même. On note $(u_n)_{n\in\mathbb N}$ cette suite, de sorte que pour tout $n\in\mathbb N$, $u_n = n$. Cette suite qui, en quelque sorte, ne fait rien, est appelée la suite identité.
Suites bijectives
Dans cette partie, je vais vous parler d’un type particulier de suite : les suites bijectives. Soit $E$ un ensemble et soit $(u_n)_{n\in\mathbb N}$ une suite à valeurs dans $E$. Autrement dit, $u:\mathbb N\to E$. La suite $u$ est dite bijective si pour tout élément $x$ appartenant à $E$, il existe un et un seul indice $n\in\mathbb N$ tel que $u_n = x$. Autrement dit, chaque élément de $E$ peut être associé à un unique entier naturel.
On peut le voir encore un peu différemment. Définir une suite bijective $(u_n)_{n\in\mathbb N}$ à valeurs dans un ensemble $E$, ce n’est rien faire d’autre que numéroter les éléments de $E$. En effet, on l’a vu, une suite bijective prend un entier et lui associe un unique élément de $E$. Bref, la suite $(u_n)_{n\in\mathbb N}$ compte les éléments de $E$.
L’exemple le plus simple de suite bijective est la suite identité $u:\mathbb N\to\mathbb N$ définie, je le rappelle, par $u_n = n$. Dans ce cas, $E = \mathbb N$ et évidemment chaque entier naturel est représenté par lui-même. Étudions un exemple plus tordu. On note $E$ l’ensemble des entiers négatifs, c’est à dire $E = \{…, -4, -3, -2, -1, 0\}$. Alors, la suite $u:\mathbb N\to E$ définie par $u_n = -n$ est une bijection. Chaque entier naturel est associé à un unique entier négatif, qui est son opposé. Réciproquement, chaque entier négatif est l’image d’un entier naturel.
Attention, attention, il y a ici une difficulté. Le caractère bijectif d’une suite dépend fortement de l’ensemble $E$ choisi. En effet, la suite définie par $u_n = n$, par exemple, est une bijection de $\mathbb N$ dans $\mathbb N$. Mais ce n’est pas une bijection de $\mathbb N\to\mathbb Z$. En effet, les entiers négatifs ne sont pas atteints par la suite $u$. Si $k$ est négatif, il n’existe aucun entier positif $n$ tel que $u_n = k$. Ainsi, $u$ n’est pas une bijection entre $\mathbb N$ et $\mathbb Z$. Cela jouera un rôle clé par la suite.
À ce stade, vous vous demandez peut-être pourquoi je vous ai parlé de suites bijectives. Le point-clé est qu’une suite bijective permet de numéroter les éléments d’un ensemble. Devinez quoi ! Dans la prochaine partie, nous allons essayer de numéroter… les nombres. C’est d’ailleurs tout l’enjeu de ce tutoriel.
Notion de fonction
Définition intuitive
Nous avons vu les suites, qui sont des opérateurs associant à chaque entier naturel, une valeur. La valeur d’arrivée peut être à peu près n’importe quoi : un nombre, un couple de nombres, éventuellement un ensemble, etc. Parlons maintenant des fonctions.
Pour ce qui nous concerne, les suites et les fonctions se ressemblent beaucoup. Une fonction, de même qu’une suite, est un opérateur qui prend une valeur et lui associe un résultat. Par exemple, l’opération qui à une voiture associe sa couleur est une fonction. On note souvent avec les lettres $f, g, h$ les fonctions.
Si $E$ et $F$ sont deux ensembles et $f$ une fonction qui à un élément de $E$ associe un élément de $F$, on note $f: E\to F$, comme pour les suites sauf que l’ensemble de départ n’est pas $\mathbb N$. En un sens, les suites sont des cas particuliers de fonctions, dont l’ensemble de départ est $\mathbb N$.
Fonction bijective
Comme pour les suites, on dit qu’une fonction $f: E\to F$ est une bijection si pour tout $y\in F$, il existe exactement un élément $x\in E$ tel que $y=f(x)$. Autrement dit, $f$ est une table d’association entre $E$ et $F$.
Il existe une fonction particulière, appelée la fonction identité. Si $E$ est un ensemble, la fonction identité est notée $Id$ et $Id: E\to E$ est la fonction qui associe à un élément de $E$, lui-même. Autrement dit, pour tout $x\in E$, $Id(x) = x$. La fonction identité est une bijection, car naturellement tout élément de $E$ admet une unique valeur par $Id$, qui est lui-même.
Dans ce tutoriel, les fonctions et les suites sont fortement similaires. La seule différence est que l’ensemble de départ d’une suite est $\mathbb N$ alors que l’ensemble de départ d’une fonction peut être n’importe quoi. Les suites seront utilisées pour établir des bijections entre l’ensemble des entiers naturels et d’autres ensembles (grâce aux suites bijectives). Les fonctions nous permettront d’établir des bijections entre des ensembles qui ne sont pas beaucoup plus compliqués que $\mathbb N$. Toutefois, ne vous fourvoyez pas : il y a des différences importantes entre les suites et les fonctions. Je vous invite à lire l’excellent tutoriel de Micmaths sur les fonctions pour en savoir davantage.
Le mot de la fin
Je vous ai un peu parlé des suites et des fonctions. Je suis allé directement à ce qui va nous servir pour la suite : les bijections. Le résultat est que ces paragraphes sont un peu secs et étranges dans leur structure. Ils ne constituent en aucun cas la finalité de ce tutoriel, mais fournissent seulement des outils pour que nous puissions comparer les tailles (au sens du nombre d’éléments) des différents ensembles de nombres.
Néanmoins, pas d’inquiétude : les notions introduites ici seront suffisantes pour aborder la suite ; je vous recommande simplement de ne pas vous précipiter.
Cardinaux et ensembles dénombrables
Quelques définitions
Cardinal d’un ensemble
Lorsque l’on travaille avec les ensembles, on aime bien connaître le nombre d’éléments qu’ils contiennent. Par exemple, l’ensemble {rouge, bleu, vert} contient trois éléments. L’ensemble {3}, qui est l’ensemble contenant 3 comme seul élément, contient un élément.
Le nombre d’éléments contenus dans un ensemble est appelé son cardinal. Si $E$ est un ensemble, on note parfois $|E|$ le cardinal de $E$, c’est la notation qui sera utilisée par la suite dans ce tutoriel. Ainsi, |{rouge, bleu, vert}| = 3, $|\varnothing| = 0$ et |{3}| = 1.
Lorsqu’un ensemble contient un nombre infini d’éléments, on utilise le symbole $\infty$. Tous les ensembles de nombres vus précédemment on un nombre infini d’éléments, on note $\infty$ leur cardinal. Je n’insiste pas là-dessus pour le moment, mais nous verrons dans quelques paragraphes que la notion de cardinal pour les ensembles infinis a un certain nombre de faiblesses.
Ensembles de même cardinal
Pour les ensembles finis, c’est facile : deux ensembles sont de même cardinal s’ils contiennent le même nombre d’éléments. Rien de bien transcendant jusque-là. Mais que dire des ensembles infinis ? Est-ce que $\mathbb N$ et $\mathbb Z$, par exemple, ont le même nombre d’éléments ? Et qu’en est-il de $\mathbb Q, \mathbb R$ ?
Comme on l’a vu, $\mathbb N\subset\mathbb Z\subset\mathbb Q\subset\mathbb R$. Notre intuition tend donc à nous dire que $|\mathbb N| < |\mathbb Z| < |\mathbb Q| < |\mathbb R|$. Pourtant, nous avons ici affaire à des valeurs qui sont toutes infinies, et il n’y a pas vraiment de sens à dire que $\infty<\infty$ (« l’infini est strictement inférieur à l’infini », c’est insensé). Ainsi, la notion de cardinal d’un ensemble n’est pas fiable pour comparer les nombres d’éléments de deux ensembles infinis.
Il nous faut une notion plus robuste. Et c’est là que la notion de bijection va nous servir. Comme vous devez vous en souvenir (ou alors, je vous invite à relire la partie précédente), on dit que deux ensembles $E$ et $F$ sont en bijection s’il existe une fonction $f: E\to F$ qui est une bijection. Ainsi, on peut identifier chaque élément de $E$ à un unique élément de $F$. Il y a donc une sorte de « table d’association » entre $E$ et $F$. C’est une bonne piste pour dire que deux ensembles infinis ont un même nombre d’éléments : chaque élément de l’un est associé à un et un seul point de l’autre.
Ainsi, notre objectif par la suite va être de savoir s’il existe des bijections entre les ensembles de nombres. S’il en existe, cela voudra dire que tous les ensembles de nombres ont exactement le même nombre d’éléments. Et si ce n’est pas le cas, alors cela voudra dire qu’il y a des ensembles infinis… plus grands que d’autres ! Sans lire la suite, essayez d’anticiper les résultats que nous allons obtenir. Je veux bien parier que vous serez surpris. 
Je ne vois pas pourquoi cette approche avec les bijections serait meilleure que celle qui consiste à dire que $\mathbb Z$ a plus d’éléments que $\mathbb N$…
Pour comprendre pourquoi c’est l’approche avec les bijections qui est la bonne, il faut revenir aux ensembles finis, et généraliser aux ensembles infinis. Comment pouvez-vous expliquer que l’ensemble {rouge, vert, bleu} a trois éléments ? La réponse est que vous avez compté, ou encore que vous avez établi une bijection entre l’ensemble {rouge, vert, bleu} et l’ensemble {1, 2, 3}. Vous pouvez aussi dire que {rouge, vert, bleu} a autant d’éléments que {Mercedes, Jaguar, Maserati}. Bref, pour dire que deux ensembles sont de même cardinal, il s’agit de les mettre en bijection. Et quand on y réfléchit vraiment, c’est bien cette approche qui est correcte, même pour les ensembles infinis. Pour savoir si deux ensembles $E$ et $F$ ont le même nombre d’éléments, il suffit de savoir associer un élément de $E$ à un élément de $F$, en n’oubliant aucun élément de part et d’autre.
Notion de dénombrabilité
On dit qu’un ensemble est dénombrable si on peut compter ses éléments. Et vu cette définition, l’ensemble dénombrable le plus facile à imaginer est… l’ensemble des nombres entiers naturels, évidemment. 0 est l’élément 1, 1 est élément 2, 2 est l’élément 3, etc. On peut énumérer tous les nombres entiers naturels dans l’ordre et les compter ainsi.
Dans le paragraphe précédent, on a vu que deux ensembles ont un même nombre d’éléments s’ils sont en bijection. On dira donc qu’un ensemble est dénombrable s’il peut être mis en bijection avec $\mathbb N$. Autrement dit, tout ensemble dans lequel on peut énumérer les éléments sera en bijection avec $\mathbb N$.
Prenons un exemple : celui des nombres entiers naturels pairs que nous avons rencontré dans la première partie. Cet ensemble est bien sûr infini. Est-il dénombrable ? Intuitivement, on dirait que oui : on peut facilement énumérer les nombres pairs : 0, 2, 4, 6, 8, 10, … Essayons d’être plus rigoureux. Souvenez-vous qu’un ensemble est dénombrable s’il peut être mis en bijection avec $\mathbb N$. On cherche donc une suite $(u_n)_{n\in\mathbb N}$ à valeurs dans $\{2n, n\in\mathbb N\}$, qui est une bijection. Essayez de la trouver, ce n’est pas si difficile. La réponse est masquée ci-dessous.
On définit $u:\mathbb N\to \{2n, n\in\mathbb N\}$ par $u_n = 2n$. Cette suite associe à chaque entier naturel, son double. Évidemment, chaque entier naturel admet un unique double et chaque entier qui est pair peut être divisé par 2. Ainsi, $u$ est une suite bijective entre l’ensemble des entiers naturels et des entiers pairs. Donc l’ensemble des entiers pairs et l’ensemble des entiers naturels contiennent exactement le même nombre d’éléments !
Je trouve ce résultat particulièrement intéressant, pour plusieurs raisons. La première, c’est qu’il est assez simple et utilise des notions assez élémentaires. Et puis, il donne un assez bon aperçu des phénomènes qui se produisent avec les ensembles infinis : dans l’ensemble des nombres pairs, on a retiré la moitié des éléments qui sont dans $\mathbb N$ et, pour autant, l’ensemble reste infini et contient le même nombre d’éléments que $\mathbb N$. Cela montre quelque chose d’assez frappant : on peut retirer un nombre infini d’éléments dans un ensemble infini, sans faire diminuer le cardinal de l’ensemble.
Ainsi donc, l’ensemble des nombres pairs est dénombrable (et infini). Donc il y a autant de nombres pairs que de nombres entiers naturels. Certes, me direz-vous, il sont tous les deux infinis… Mais attendez la suite.
Quelques ensembles dénombrables
Pour le moment, nous n’avons pas vu de choses extrêmement surprenantes — enfin, un peu quand même, mais pas de quoi s’arracher les cheveux. Nous allons continuer notre voyage à travers les ensembles infinis.
L’ensemble des nombres relatifs
Nous allons regarder si l’ensemble $\mathbb Z$ est dénombrable. Rappelez-vous que $\mathbb Z = \{…, -4, -3, -2, -1, 0, 1, 2, 3, …\}$. Rappelez-vous également qu’un ensemble est dit dénombrable s’il existe une suite bijective à valeurs dans cet ensemble. Pour montrer que $\mathbb Z$ est dénombrable, il s’agit donc de trouver une suite $u: \mathbb N\to\mathbb Z$ qui soit bijective. La question est d’abord de savoir si une telle suite existe. D’après vous, est-ce le cas ?
Le fait que ces paragraphes soient placés dans la section « Quelques ensembles dénombrables » est normalement un bon indice… Et en effet, une telle suite existe. Ce n’est pas très évident, mais je vous invite à essayer de la trouver. Je masque la réponse ci-dessous.
On définit $u:\mathbb N\to\mathbb Z$ par $u_n = \frac n2$ si $n$ est un nombre pair, et par $u_n = \frac{-n-1}{2}$ si $n$ est un nombre impair. Par exemple, $u_0 = \frac02 = 0$, car 0 est pair. En revanche, $u_{19} = \frac{-19-1}{2} = \frac{-20}{2} = -10$, car 19 est impair.
Je suppose à partir d’ici que vous avez lu la solution, donc que vous connaissez la suite $u$ que j’ai choisie. Notez bien que cette suite n’est pas unique, il en existe plusieurs. Avant de démontrer vraiment que cette suite $(u_n)_{n\in\mathbb N}$ est bijective, calculons ses premiers termes pour avoir une idée de son comportement :
| $n$ | $u_n$ |
|---|---|
| 0 | 0 |
| 1 | -1 |
| 2 | 1 |
| 3 | -2 |
| 4 | 2 |
| 5 | -3 |
| 6 | 3 |
Démontrons que $u$ est bijective. Tout d’abord, assurons-nous qu’elle prend effectivement ses valeurs dans $\mathbb Z$. Autrement dit, il s’agit de vérifier que quel que soit $n\in\mathbb N$, $u_n$ est un nombre relatif. Il est possible, a priori, que $u_n$ ne soit pas un nombre entier. Il faut démontrer que c’est bien le cas. On distingue deux cas, selon la parité de $n$. Si $n$ est un nombre pair, alors $u_n = \frac n2$, qui est un nombre entier naturel étant donné que $n$ peut être divisé par 2. Donc, si $n$ est pair, $u_n\in\mathbb N$ donc $u_n\in\mathbb Z$. Si maintenant $n$ est impair, alors $u_n = \frac{-n-1}{2}$. Mais $-n-1$ est alors un nombre pair, donc $\frac{-n-1}{2}$ est un nombre entier. Donc $\frac{-n-1}{2}\in\mathbb Z$. Ainsi, il est vrai que la suite $u$ est à valeurs dans $\mathbb Z$.
Maintenant, il faut montrer que $u$ est une bijection, autrement dit que pour tout $k\in\mathbb Z$, il existe un unique $n\in\mathbb N$ tel que $u_n = k$. Soit donc $k$ un nombre entier relatif. On distingue deux cas, selon le signe de $k$.
Si $k$ est positif ($k\ge 0)$, alors $u_{2k} = \frac{2k}{2} = k$. Ainsi, il existe bien un entier naturel $n$, à savoir $n=2k$, tel que $u_n = k$.
Si maintenant $k<0$, on pose $n = -2k-1$. Comme $k<0$, $-2k\ge 2$, donc $-2k-1\ge 1$. Donc $n\in\mathbb N$. De plus, $u_n = u_{-2k-1} = \frac{-(-2k-1)-1}{2} = \frac{2k+1-1}{2} = \frac{2k}{2} = k$. Donc on a trouvé un entier naturel $n$, ici $n = -2k-1$, tel que $u_n = k$.
Au final, n’importe quel entier relatif est bien une valeur prise par la suite $u$. Reste à démontrer que cette valeur est atteinte pour un seul entier naturel $n$. Pour ce faire, fixons $k\in\mathbb Z$. On sait qu’il existe $n\in\mathbb N$ tel que $u_n = k$. On veut montrer que $n$ est unique. Ce n’est pas certain a priori : il se peut que deux indices $m$ et $n$ distincts soient tels que $u_m = u_n$. Supposons que ce soit le cas et qu’il existe justement $m, n$ deux entiers naturels tel que $u_m = u_n$. On note $k$ cette valeur. À nouveau, on distingue deux cas : soit $k\ge 0$, soit $k<0$. Si $k$ est positif, alors $u_m = \frac{-m-1}{2} = k$ et $u_n = \frac{-n-1}{2} = k$. Mais alors, $\frac{-m-1}{2} = \frac{-n-1}{2}$ donc $-m-1 = -n-1$ et donc $m=n$. Ainsi, si $u_m=u_n$, alors $m=n$. Étudions maintenant le cas où $k>0$. Alors, $u_m = \frac m2 = k$ et $u_n = \frac n2 = k$, donc $\frac m2 = \frac n2$ et donc $m=n$, comme précédemment.
En fin de compte, la suite $(u_n)_{n\in\mathbb N}$ est une bijection à valeurs dans $\mathbb Z$. Conclusion : $\mathbb Z$ est dénombrable, au même titre que $\mathbb N$. Ainsi, l’ensemble des entiers relatifs, qui a l’air de contenir deux fois plus d’éléments que l’ensemble des entiers naturels, en contient en fait autant, ni plus, ni moins.
L’ensemble des nombres rationnels
Nous allons maintenant montrer que l’ensemble $\mathbb Q$ des nombres rationnels est lui aussi dénombrable. Je vous rappelle pour cela que nous avons défini cet ensemble par $\mathbb Q = \{\frac pq, p\in\mathbb Z, q\in\mathbb N, q\not=0, p\wedge q = 1\}$. Cette définition assure que la donnée d’un nombre rationnel $\frac pq$ est équivalente à la donnée d’un entier relatif $p$ et d’un entier naturel non nul $q$. Autrement dit, donner une fraction $\frac pq$, c’est donner un couple $(p, q)\in\mathbb Z\times\mathbb N^*$ où $p$ et $q$ sont les plus simples possibles.
Que désigne la notation $\mathbb N^*$ ?
En effet, je n’ai pas introduit cette notation précédemment. $\mathbb N^*$ est l’ensemble $\mathbb N$ privé de $0$. Autrement dit, $\mathbb N^* = \{1, 2, 3, …\}$. On a vu que $\mathbb Q$ et $\mathbb Z\times\mathbb N^*$ sont deux notations pour le même ensemble. Plus précisément, $\mathbb Z\times\mathbb N$ contient les rationnels, certains en plusieurs exemplaires. Dit autrement, on peut voir $\mathbb Q$ comme étant un ensemble inclus dans $\mathbb Z\times\mathbb N^*$. Pour montrer que $\mathbb Q$ est dénombrable, il suffit donc de montrer que $\mathbb Z\times \mathbb N^*$ l’est. Or, on a déjà vu que $\mathbb Z$ est dénombrable, i.e. que $\mathbb Z$ et $\mathbb N$ sont de même cardinal. Donc, pour montrer que $\mathbb Z\times\mathbb N^*$ est dénombrable, il suffit de montrer que $\mathbb N\times \mathbb N^*$ est dénombrable.
On a bien simplifié le problème ! Pour montrer que $\mathbb Q$, qui est un ensemble de fractions, est dénombrable, il suffit de montrer que l’ensemble $\mathbb N\times\mathbb N^*$ est dénombrable. Rappelons que l’ensemble $\mathbb N\times \mathbb N^*$ est l’ensemble des couples $(p, q)$ avec $p\in\mathbb N$ et $q\in\mathbb N^*$, ce qui est bien plus facile à étudier que $\mathbb Q$.
Pour montrer que $\mathbb N\times\mathbb N^*$ est dénombrable, nous allons étudier un dessin. En effet, c’est la meilleure manière de comprendre de quoi l’on parle, et ici des formules apporteraient davantage de confusion que de clarté. Savez-vous comment l’ensemble $\mathbb N\times\mathbb N^*$ peut se représenter graphiquement ? Cela ressemble à l’ensemble $\mathbb N\times\mathbb N$ vu au début de ce tutoriel :
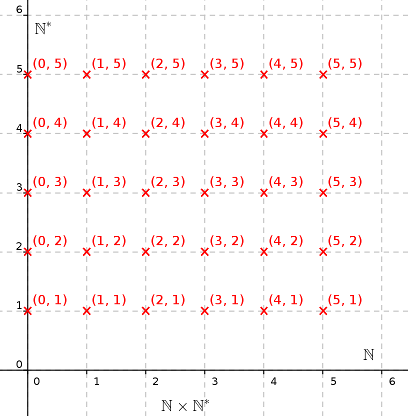
Chaque couple $(p, q)\in\mathbb N\times\mathbb N^*$ s’interprète comme la fraction $\frac pq$, où $p$ se lit sur l’axe horizontal et $q$ sur l’axe vertical. Pour montrer que $\mathbb N\times\mathbb N^*$ est dénombrable, il ne reste qu’à trouver une suite $u:\mathbb N\to\mathbb N\times \mathbb N^*$. Et ça, c’est plutôt facile ! Il suffit simplement de parcourir en zigzags la grille, en attribuant un numéro à chaque croix rouge rencontrée. Une belle image vaut mieux qu’un long discours, dans ce genre de situations !
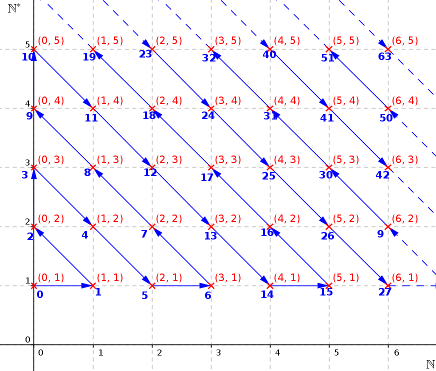
À chaque nombre entier naturel $n$ écrit en bleu sur l’image, on associe un et un seul élément de $\mathbb N\times \mathbb N^*$ de manière bijective. Ce dessin est infini et recouvre tous les couples de points. On parcourt ainsi l’ensemble $\mathbb N\times\mathbb N^*$ en zigzag, et on associe un numéro à chacun de ses éléments. Ceci construit une suite bijective à valeurs dans $\mathbb N\times\mathbb N^*$. Or, $\mathbb N\times\mathbb N^*$ et $\mathbb N\times\mathbb Z^*$ sont aussi en bijection, et de plus on a vu que $\mathbb Q$ et $\mathbb Z\times\mathbb N^*$ désignent le même ensemble (modulo les fractions irréductibles). On en déduit que $\mathbb N$ et $\mathbb Q$ sont en bijection, donc que $\mathbb Q$ est dénombrable…
En plus, nous avons évité une difficulté importante, liée à la multiplicité des façons de représenter un rationnel. Nous avons beaucoup travaillé au moment où nous avons défini l’ensemble $\mathbb Q$ pour éviter les doublons, et pour pouvoir interpréter $\mathbb Q$ comme une partie de $\mathbb Z\times\mathbb N^*$. Ensuite, nous avons dénombré $\mathbb N\times\mathbb N^*$, ce qui n’est pas très difficile, et cela suffit à conclure que $\mathbb Q$ est dénombrable.
Pour certains mathématiciens, le dessin que j’ai fait ne saurait tenir lieu de démonstration valable mathématiquement. Pourtant, nous allons nous en contenter dans le cadre de ce tutoriel. Sachez qu’il y a une formule explicite pour la suite que nous avons construite, mais elle est compliquée et à mon avis pas vraiment éclairante pour comprendre de quoi l’on parle. C’est pourquoi j’ai choisi de ne pas l’évoquer. Il y a plein d’infos sur Wikipédia. À mon sens toutefois, ce genre de dessins suffit à établir la démonstration : il n’y a pas d’ambiguïté et pas d’argument fallacieux caché dans l’illustration.
Ceci clôture cette partie. Nous avons vu que $\mathbb N$ et $\mathbb Z$ sont dénombrables. De manière un peu plus surprenante, nous avons aussi démontré que $\mathbb Q$ est aussi dénombrable, alors que d’apparence, les nombres rationnels ont l’air bien plus nombreux. Nous allons maintenant passer à l’étude de l’ensemble $\mathbb R$ des nombres réels.
Vers l'infini, et au-délà
Dénombrabilité et non dénombrabilité
Jusqu’ici, nous avons mis au point un critère pour comparer deux ensembles. Ce critère est celui de la bijection : si deux ensembles sont en bijections (par exemple $\mathbb{N}$ et $\mathbb{Z})$ alors on dit qu’ils ont le même nombre d’éléments.
La question légitime à se poser est la suivante : y-a-t-il des ensembles qui ne sont pas en bijection ?
Bien sûr, vous connaissez déjà la réponse pour les ensembles finis : deux ensembles finis sont en bijection si, et seulement si, ils ont le même nombre d’éléments (au sens usuel). En particulier, vous connaissez plein d’exemples d’ensembles finis qui ne sont pas en bijection. Par exemple $\{1\}$ et $\{1,2\}$ ne sont pas en bijection. Mais la question se pose pour les ensembles infinis.
On se ramène donc à essayer de trouver des ensembles infinis qui ne sont pas en bijection avec $\mathbb N$, par exemple. De tels ensembles sont dits non dénombrables, et a priori les exemples manquent. Le but de cette partie est donc le suivant. On va montrer que l’ensemble des nombres réels est indénombrable, et donc qu’il est « vraiment » beaucoup plus gros que celui des rationnels ou des entiers (qui sont les mêmes, à bijection près). Dit de manière plus provocante (et, avouons-le, un peu plus spectaculaire), nous allons démontrer qu’il existe des infinis de différentes tailles.
Retour sur la définition de $\mathbb{R}$
Avant de s’attaquer à montrer que $\mathbb{R}$ n’est pas dénombrable, encore faut-il lui donner une description que l’on puisse manipuler.
Le choix effectué est le suivant. L’ensemble $\mathbb{R}$ des nombres réels est l’ensemble des écritures décimales $$ x = n.d_1d_2d_3\dots $$,
où $n$ est un entier relatif et les $d_1,d_2,\dots$ sont des entiers compris entre $0$ et $9$. Plus informellement, l’ensemble $\mathbb R$ est l’ensemble de tous les nombres à virgule possibles, y compris ceux pour lesquels l’écriture est totalement imprévisible. Néanmoins, une question se pose : est-il vraiment certain qu’un nombre réel s’écrive de manière unique de la manière définie ci-dessus ?
La réponse est non, et donc a priori, cette écriture est mauvaise. Par exemple, on peut montrer que $0.999\dots = 1$ (sauriez-vous le montrer — ce n’est pas évident, mais si vous avez connaissance de la notion de série convergente, c’est à votre portée — ?). Heureusement, il y a une parade efficace, et c’est la suivante. On demande à ce que pour tout $n$ entier fixé, il existe $k\geq n$ tel que $d_k\neq 9$. En d’autres termes, on interdit que la suite des décimales soit identique à $9$ après un certain nombre de premières décimales.
On dira alors que $(n,d_1,d_2,d_3,\dots)$ est un développement décimal propre du nombre réel $x$. Typiquement, l’écriture $1$ est le développement décimal propre du réel $0.999…$, et ce développement est unique. De manière plus générale, on peut démontrer que tout réel $x$ admet un unique développement décimal propre. Ainsi, lors du comptage des nombres réels, on saura éviter les doublons. On définit donc l’ensemble $\mathbb{R}$ comme étant exactement l’ensemble des développements décimaux propres.
Diagonale de Cantor
On peut enfin procéder à la démonstration. Tout d’abord, on va se ramener au cas de l’intervalle $[0,1[$. En effet, si on peut montrer que $[0,1[$ n’est pas dénombrable, alors il en est nécessairement de même pour $\mathbb{R}$ (puisque le second contient le premier).
La méthode est la suivante. On va montrer que toute partie dénombrable de $[0,1[$ évite un élément de $[0,1[$. En d’autres termes, toutes les parties dénombrables de $[0,1[$ sont strictement incluses dans $[0,1[$. Et donc $[0,1[$ ne peut pas être dénombrable (sinon, il serait lui-même une partie de $[0,1[$ qui ne serait pas strictement incluse dans $[0,1[$). L’argument utilisé est communément appelé celui de la « diagonale de Cantor ». Le principe est très semblable à celui que vous avez rencontré précédemment.
Toute partie dénombrable de $[0,1[$ peut être écrite comme une suite d’éléments de $[0,1[$, par définition de la dénombrabilité. Par exemple si $f:\mathbb{N}\to [0,1[$ est une bijection, on peut prendre la suite $(f(n))_{n\in\mathbb{N}}$. Donnons-nous donc $(r_n)_{n\in \mathbb{N}^*} = (r_1,r_2,\dots)$ une suite d’éléments $[0,1[$.
On va maintenant exhiber un $x\in [0,1[$ qui n’est pas dans cette suite. Pour ce faire, on définit ses décimales : soit $n$ est un entier naturel non nul, la $n$-ième décimale de $x$ est choisie pour être un nombre différent de la $n$-ième décimale de $r_n$. Comme il y a 10 décimales possibles, on peut toujours en choisir une, et faire en sorte que le développement décimal soit propre (en fait on peut toujours en choisir une parmi les 9 premières et non les 10).
Ainsi donc, la $n$-ième décimale de $x$ assure que $x$ est différent de $r_n$, pour tout entier naturel $n$ non nul. Autrement dit, pour tout $n\in\mathbb{N}^*$, $x\not=r_n$, et donc $x$ n’est pas un élément de la suite $(r_n)_{n\in\mathbb{N}^*}$.
On a donc montré que la suite $(r_n)_{n\in\mathbb{N}^*}$ évite nécessairement un élément de $[0, 1[$. Mais la suite $(r_n)_{n\in\mathbb{N}}$ est une partie dénombrable quelconque, et donc toute partie dénombrable de $[0,1[$ évite au moins un point. Donc $[0,1[$ est indénombrable et $\mathbb{R}$ aussi.
O.K., ta preuve me convient. Mais pourquoi l’argument est-il appelé argument diagonal ?
Tout d’abord, il ne s’agit que d’un point de vocabulaire, on aurait pu choisir un autre nom. Toutefois, l’idée reste assez géométrique. En effet, reprenons notre suite $(r_n)_{n\in\mathbb N^*}$ d’éléments de $[0, 1[$. Quel que soit $n\in\mathbb N^*$, $r_n$ admet un unique développement décimal propre. On peut donc écrire les éléments de la suite les uns en dessous des autres, de la manière suivante : $ r_1 = 0.r_{1,1}r_{1,2}r_{1,3}r_{1,4}…\ r_2 = 0.r_{2,1}r_{2,2}r_{2,3}r_{2,4}…\ r_3 = 0.r_{3,1}r_{3,2}r_{3,3}r_{3,4}…\ r_4 = 0.r_{4,1}r_{4,2}r_{4,3}r_{4,4}…$
Avec ces notations, $r_{i,j}$ désigne la $j$-ième décimale de $r_i$, pour $(i, j)\in\mathbb N^*\times\mathbb N^*$.
Lorsque l’on construit $x$, on demande que sa $i$-ième décimale $x_i$ soit différente de la $i$-ième décimale de $r_i$, i.e. on demande que $x_i\not=r_{i,i}$. Géométriquement, les décimales de $x$ doivent éviter la diagonale des $(r_{i,i})_{i\in \mathbb{N}^*}$.
Le mot de la fin
Ce tutoriel touche à sa fin ; il faut dire qu’il a été plutôt long. Nous avons fait beaucoup de choses, et des choses plutôt déconcertantes. L’objectif, souvenez-vous, était d’évaluer la taille des ensembles de nombres, le mot « taille » devant ici s’entendre au sens du nombre d’éléments.
Seulement, la notion de « nombre d’éléments » a une faille majeure : elle tombe en défaut pour le cas des ensembles infinis. Nous avons donc expliqué que deux ensembles infinis sont de cardinaux égaux si et seulement s’ils sont en bijection. Ainsi, les ensembles $\mathbb N$, $\mathbb Z$ et, de manière un peu plus surprenante, $\mathbb Q$, sont en bijection, et on dit qu’ils sont dénombrables. Par contre, l’ensemble des nombres réels $\mathbb R$, lui, n’est pas dénombrable. Ce résultat a pour conséquence que les infinis peuvent être de tailles différentes.
Comme vous le voyez, les mathématiques sont pleines de surprises, et il est possible d’étudier des phénomènes mathématiques compliqués avec peu de connaissances de base. Gageons que ce tutoriel en est une illustration, et j’espère qu’il vous aura intéressé, diverti et amusé.
Licence et droits d’auteur
Ce tutoriel est publié sous licence CC BY-SA. Vous avez le droit, et c’est encouragé, de copier ce tutoriel, de le partager et de le modifier à votre guise. Il vous est seulement demandé de citer mon pseudonyme et de conserver la même licence d’utilisation.
Illustration du tutoriel
Comme vous l’aurez remarqué, l’illustration du tutoriel est moche et pas tellement représentative de ce que l’on y apprend. Si vous avez davantage de talent que moi, du temps et envie de me proposer une image pour illustrer le tutoriel, je suis preneur : vous pouvez m’envoyer un message privé ou poster directement dans les commentaires vos propositions. 
Quelques remerciements
Je remercie chaleureusement Holosmos, qui a pris de son temps pour relire ce tutoriel et pour m’aider à en voir le bout. C’est notamment lui qui m’a remotivé pour arriver à rédiger la dernière section, sur la non dénombrabilité de l’ensemble $\mathbb R$. Ses commentaires ont toujours été pertinents et m’ont permis de sensiblement améliorer certains points parfois difficiles à expliquer en termes simples.







