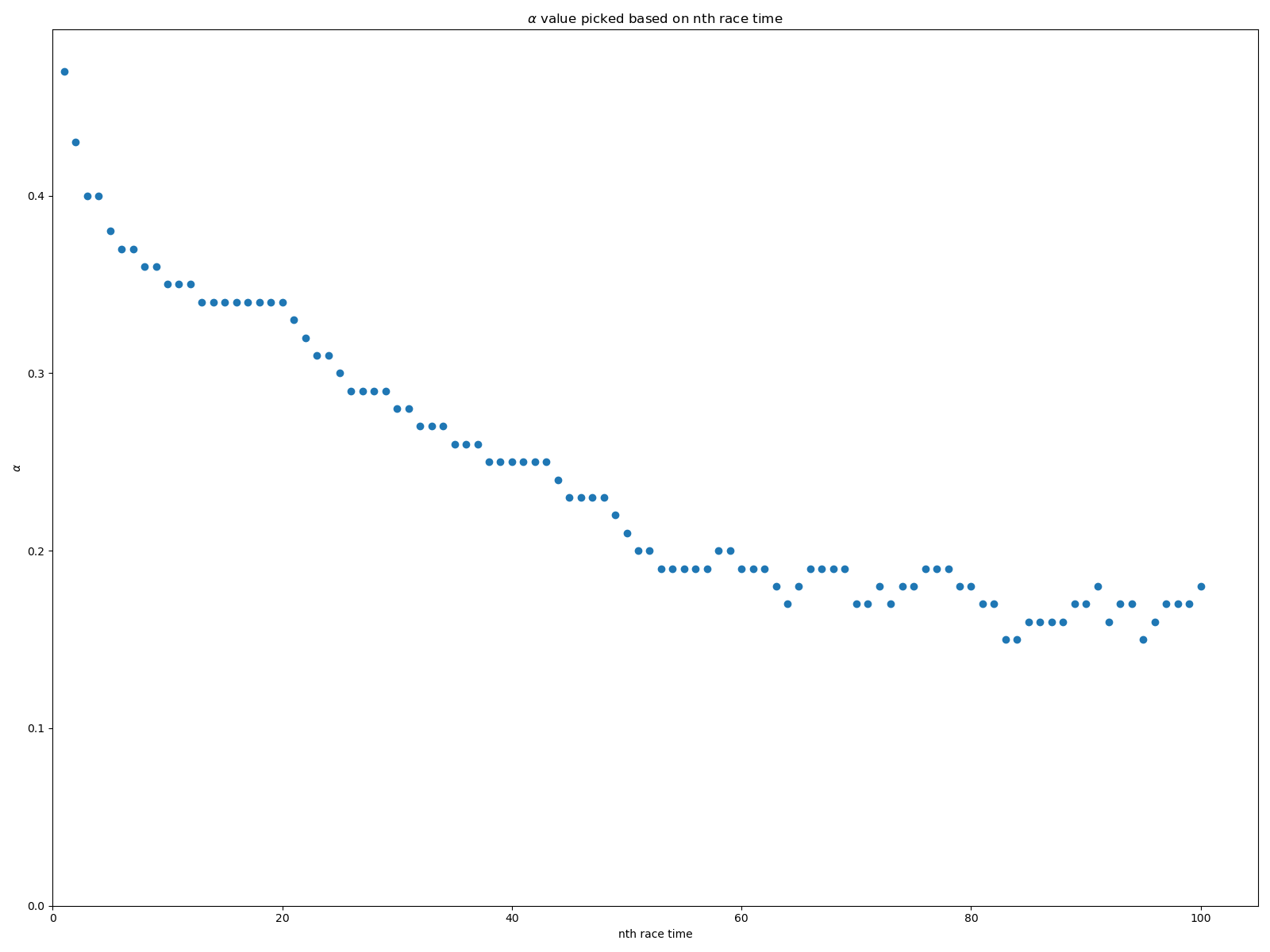
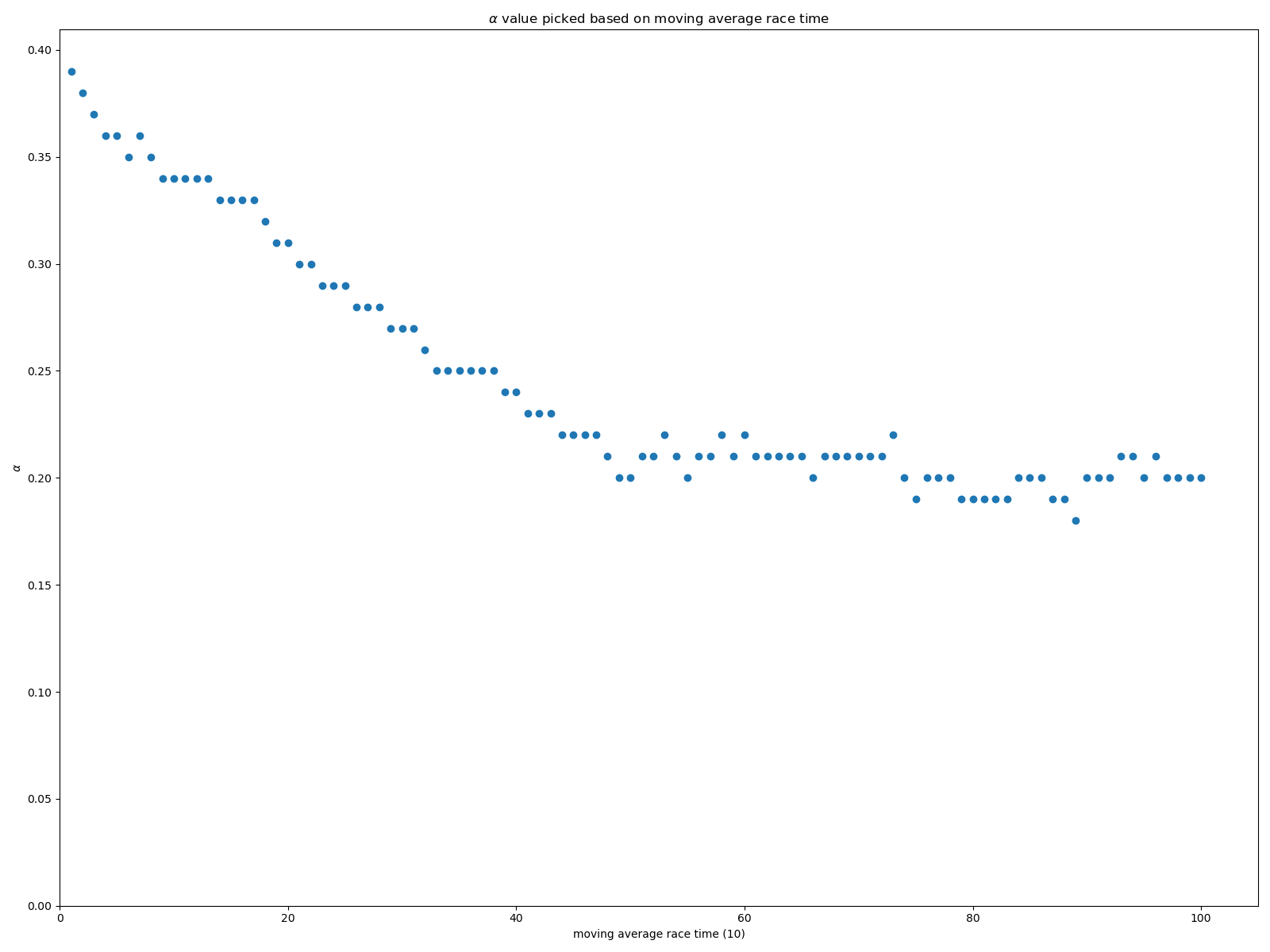
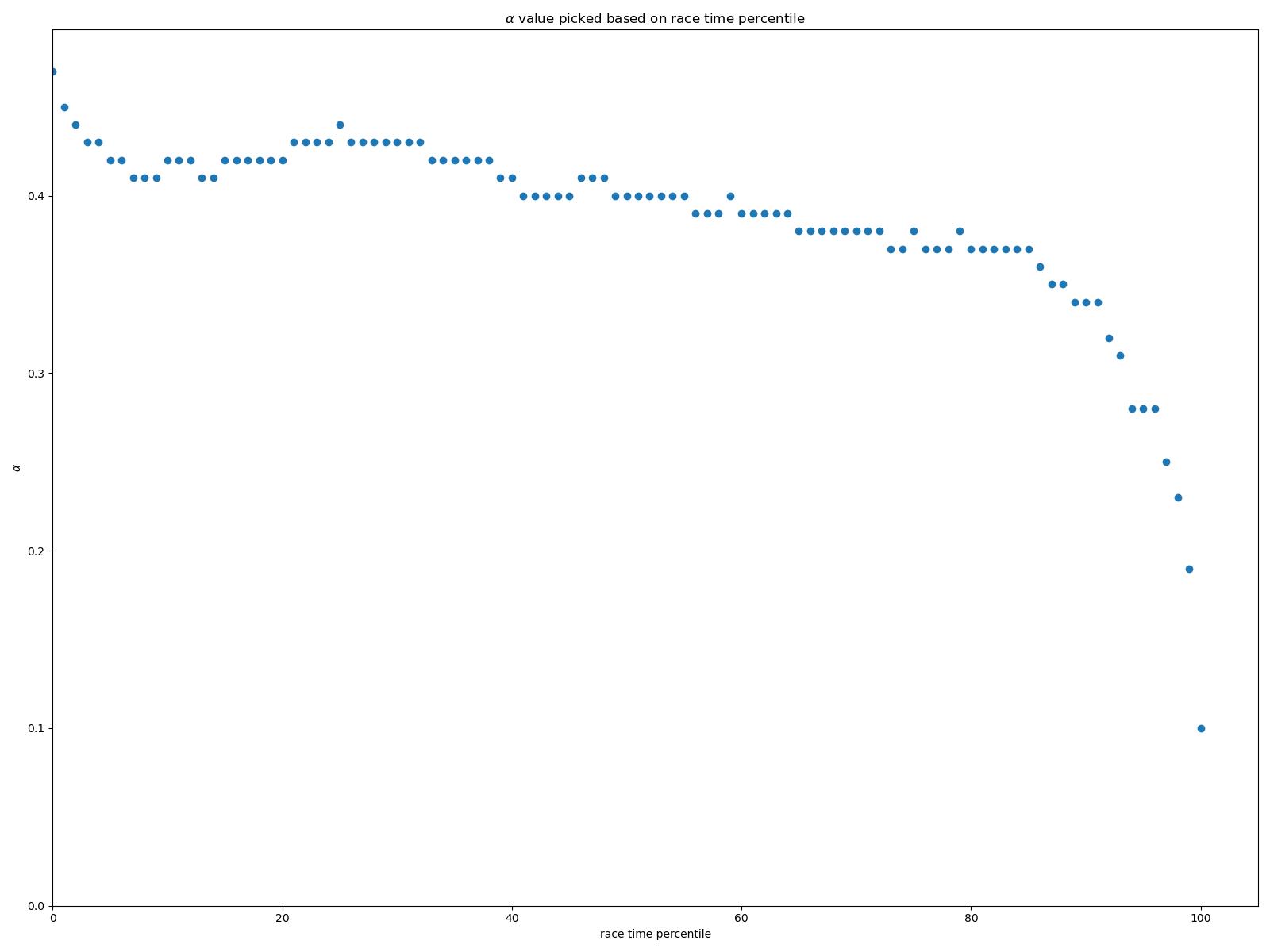
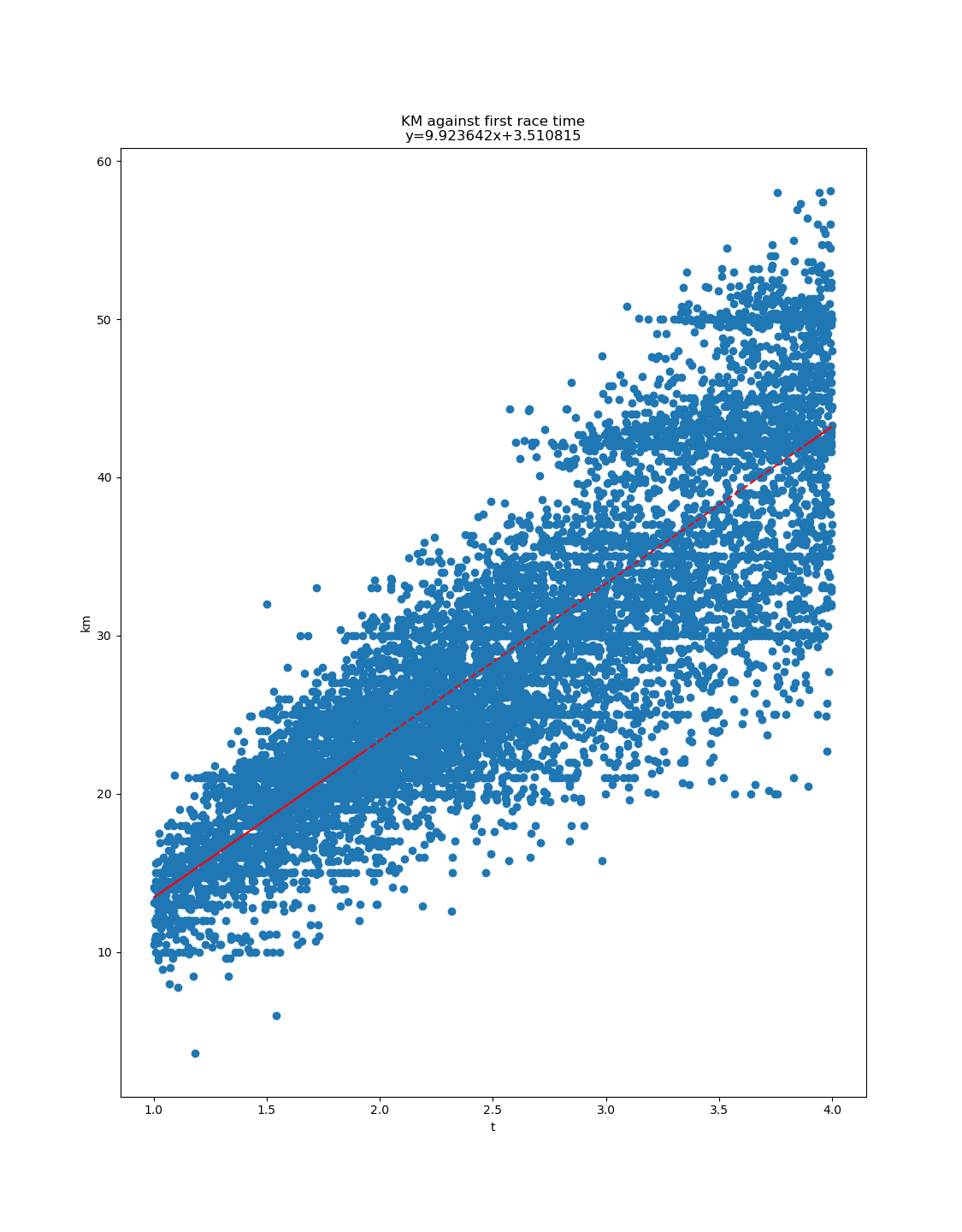
- tleb,
Salut à tous,
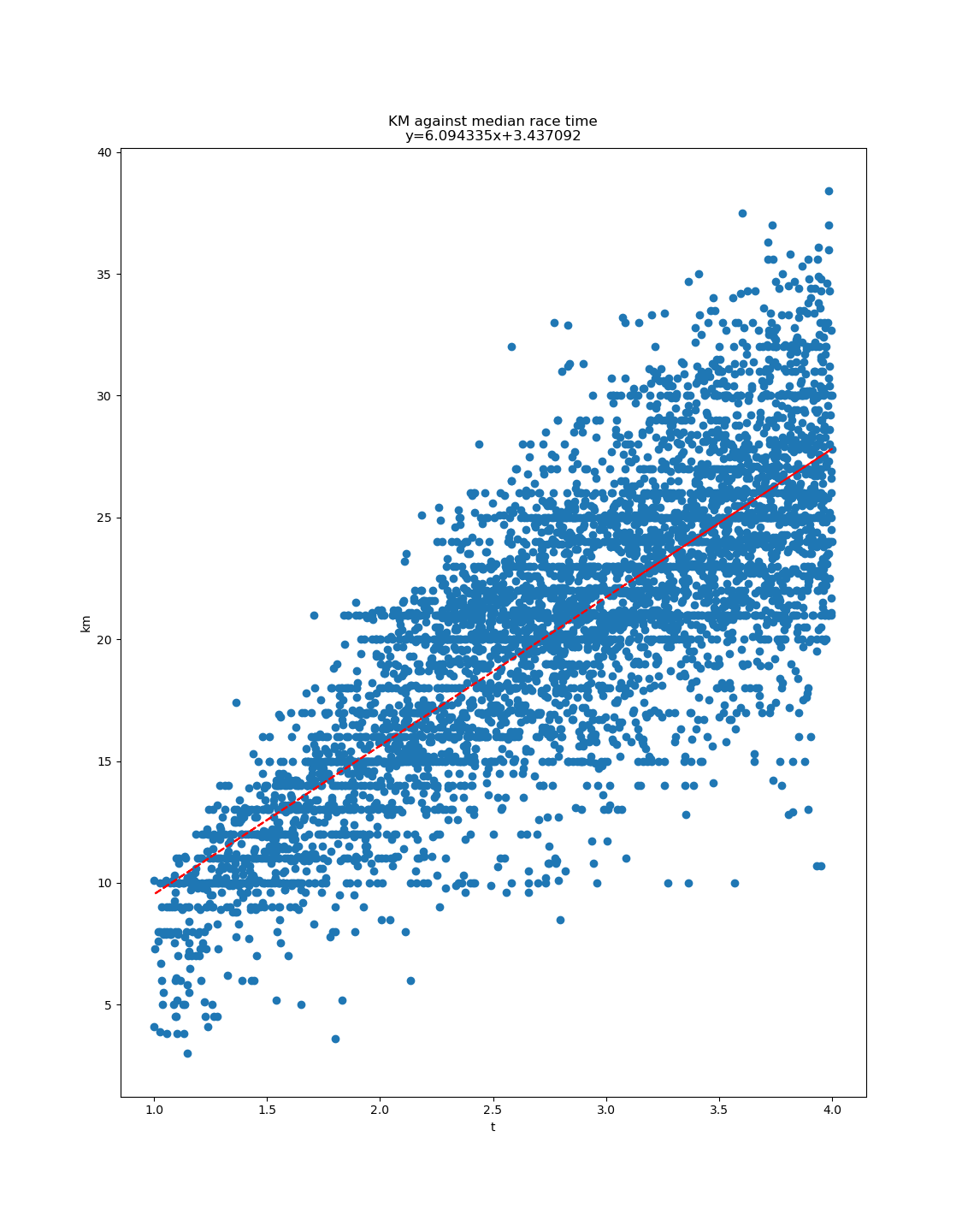
Il m’est venu aujourd’hui la question suivante : que vaut l’estimation commune du "kilomètre-effort" d’une course ?
C’est un concept primitif pour estimer la difficulté d’une course à pied. Le but est d’avoir une mesure qui prend en compte le dénivelé positif, pour avoir quelque chose de plus représentatif que simplement le nombre de kilomètres.
On prend km la longueur du parcours en kilomètres et D+ son dénivelé positif en mètres, et on estime :
kme=km+100D+
En gros, on estime que 100m de D+ vaut 1km. C’est vraiment pratique comme estimation, mais c’est proche de la réalité au moins ?
J’ai eu une démarche pour calculer ça, et j’ai obtenu un résultat. Je partage ici pour avoir des retours sur la démarche. Vous voyez des erreurs ? Vous auriez pris des raccourcis ?
Voici donc la démarche :
Le problème est que km est une mauvaise estimation de l’effort à fournir. Le but est de trouver une meilleure approximation à base de D+.
D’abord, il faudrait savoir ce qu’est "un effort" pour pouvoir le quantifier et y comparer différentes estimations. Le temps semble être pas mal. Si c’est facile, on va plus vite ce qui montre que l’effort est moindre. Sinon, on ralenti et on réparti notre effort sur une plus longue période. L’avantage, c’est que c’est une donnée facilement obtenable des courses.
Donc, en supposant qu’on obtient plein de triplets (km,D+,t), avec t le temps passé, on en fait quoi ?
On cherche une meilleure estimation de l’effort que kme, mais la forme qu’il a semble logique :
kme′=km+100αD+
On se demande si α=1 est la meilleure solution. Donc, on suppose que kme′×β=t, càd qu’ils grandissent ensemble de manière linéaire.
Pour ça, je me dis qu’on peut faire une estimation linéaire entre t et kme′ pour différentes valeurs de α. L’estimation qui aura la plus petite erreur sera la plus adaptée.
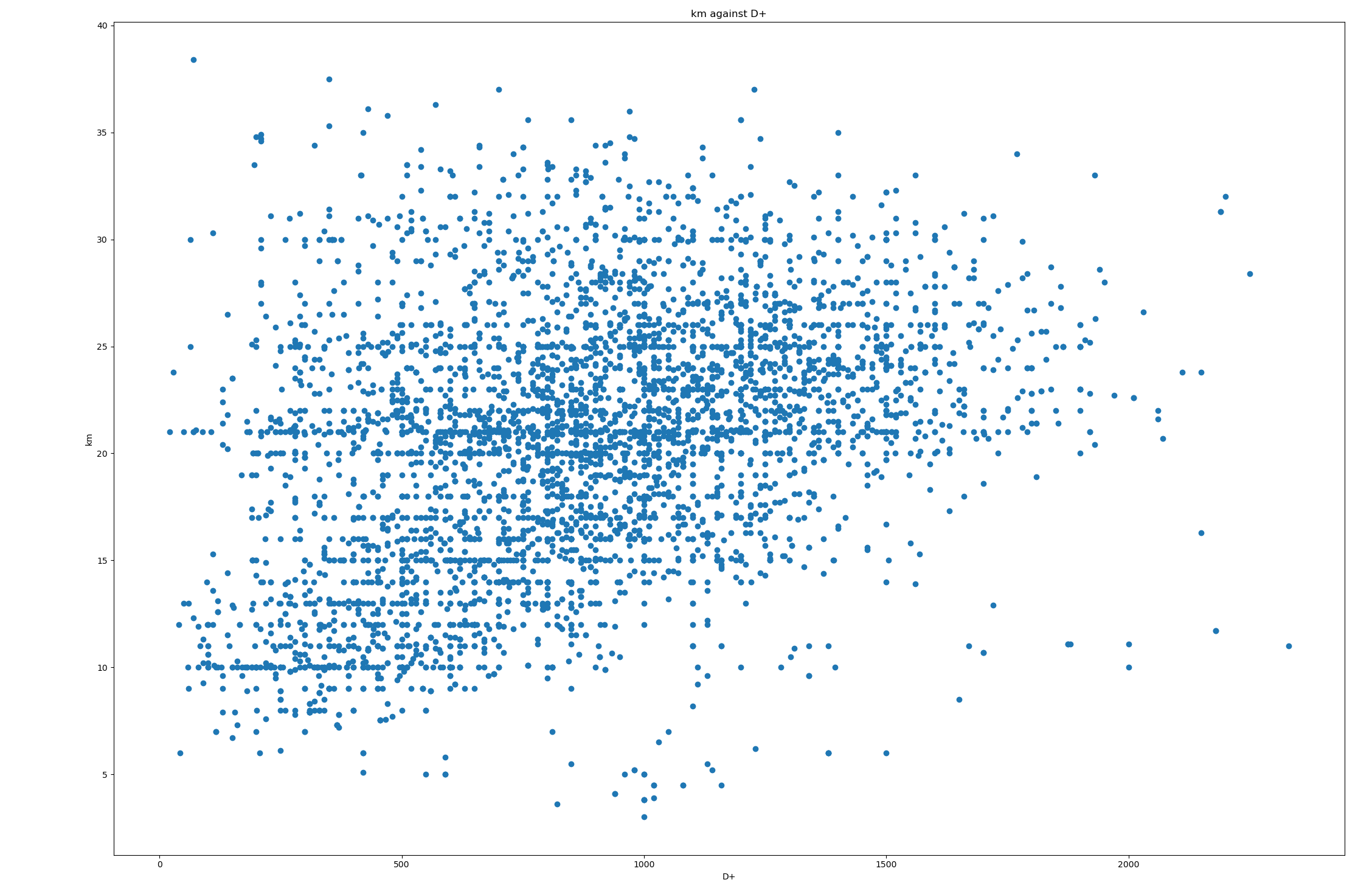
Donc maintenant, on passe au concret. On télécharge des données de courses du site de l'UTMB, qui recense beaucoup de course (34505 courses).
Pour chaque course, on extrait uniquement (1) la distance, (2) le D+ et (3) le temps médian. Pour ce dernier, je n’ai pas de bonne justification. Il me fallait un temps, et le médian m’a semblé le plus adapté (surtout pour éviter les extrêmes). J’ignore les courses :
- avec moins de 50 temps,
- de moins d’une heure,
- de plus de 4 heures,
- avec du D+ de moins de 10m (soucis de saisie de données).
Ensuite, pour les valeurs de α entre 0 et 1.5 avec un pas de 0.01, on fait ça :
x = data[:,2] # t
y = (data[:,0] + (data[:,1] * alpha / 100)) # km + (dplus * alpha / 100)
_, a, _, _, _ = np.polyfit(x, y, 1, full=True)
error = a[0]
On utilise la "méthode des moindres carrés" avec un degré 1 pour viser une droite. On récupère ce que la documentation NumPy appelle "residuals – sum of squared residuals of the least squares fit".
(Une autre technique si on n’a pas un nombre décimal représentant l’erreur est de diviser y par le temps. Comme ça, on vise à minimiser le polynôme de degré 1 parce qu’on sait que l’estimation qu’on désire est une droite parallèle à l’axe des abscisse.)
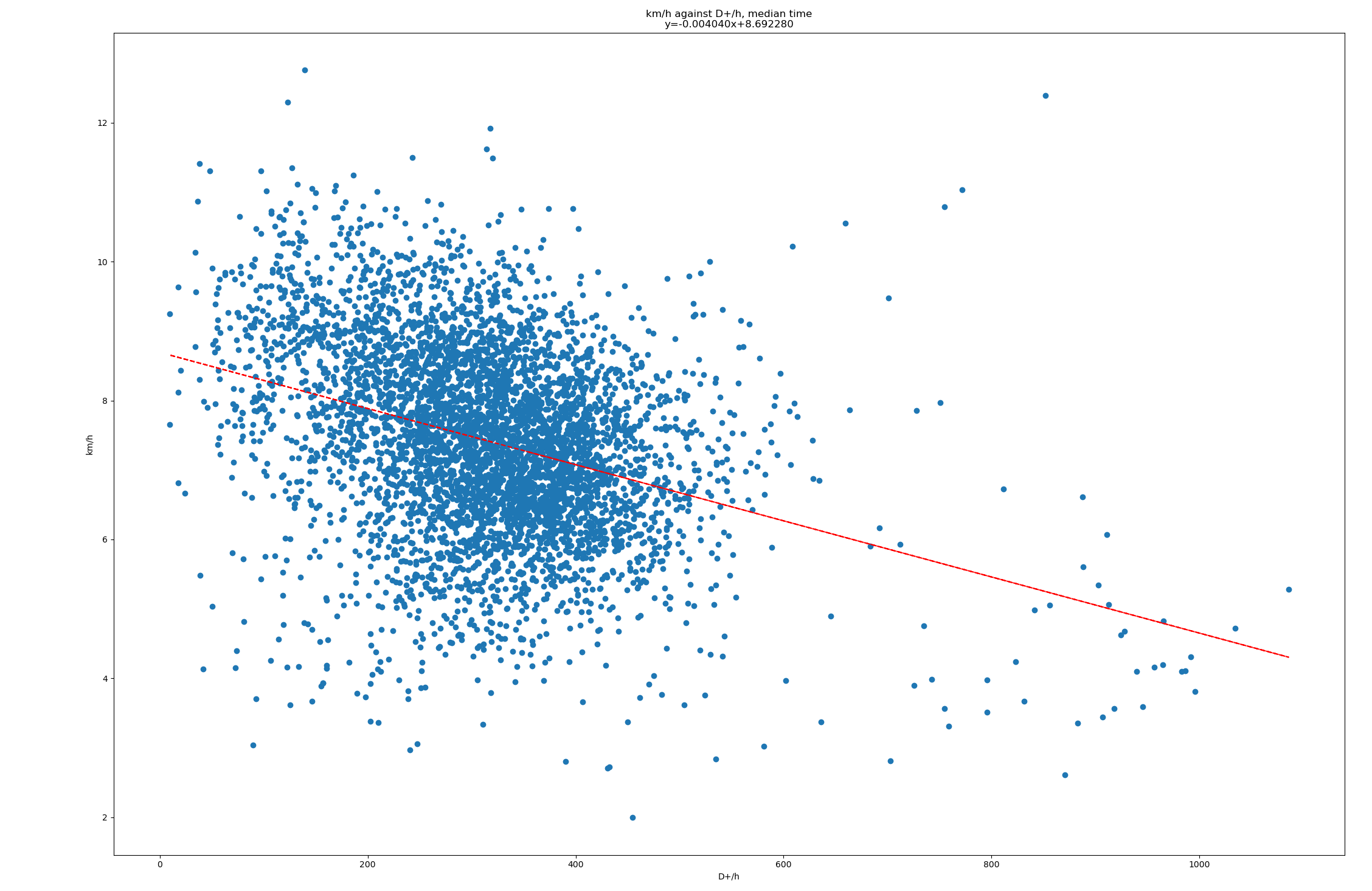
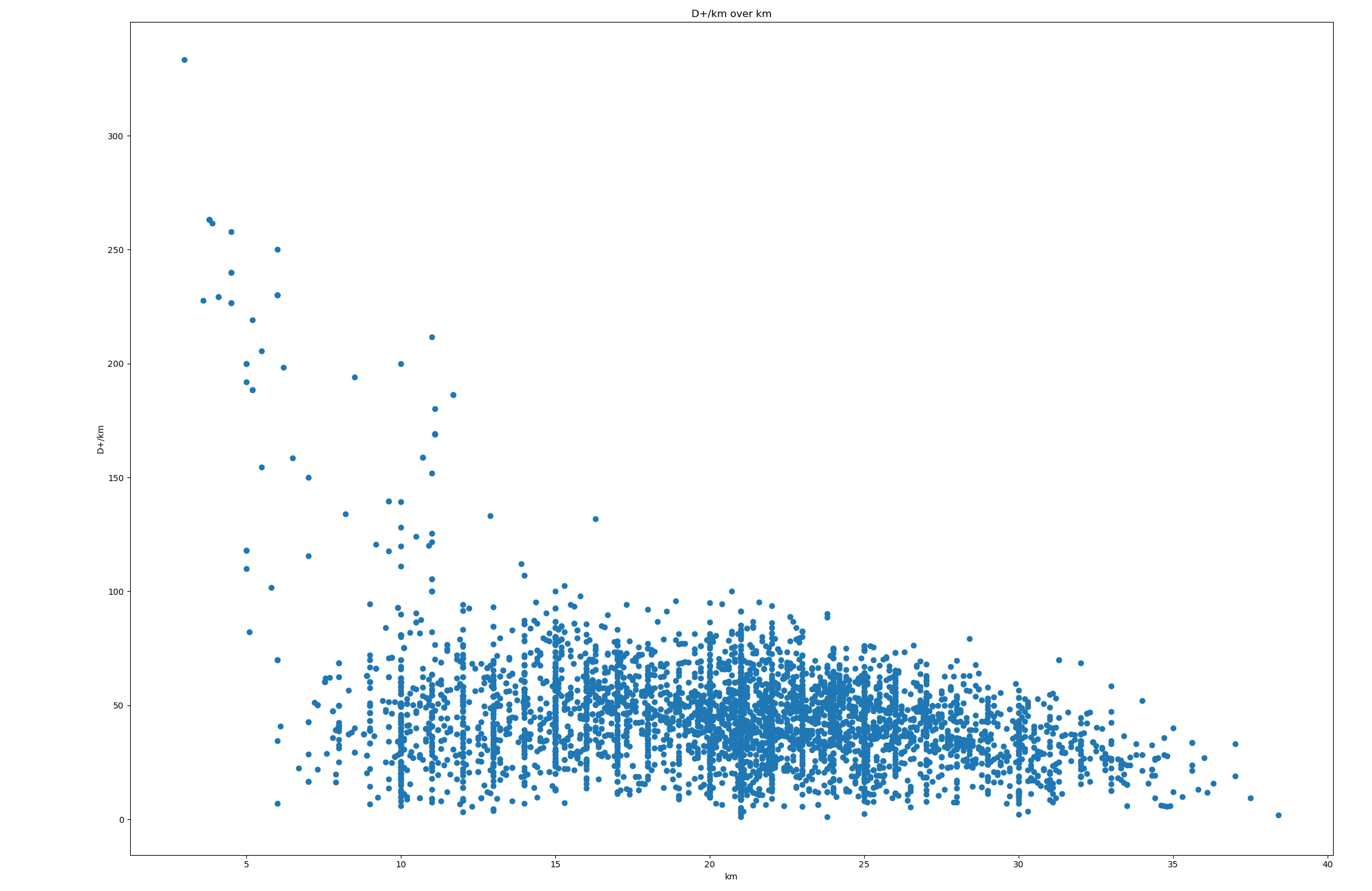
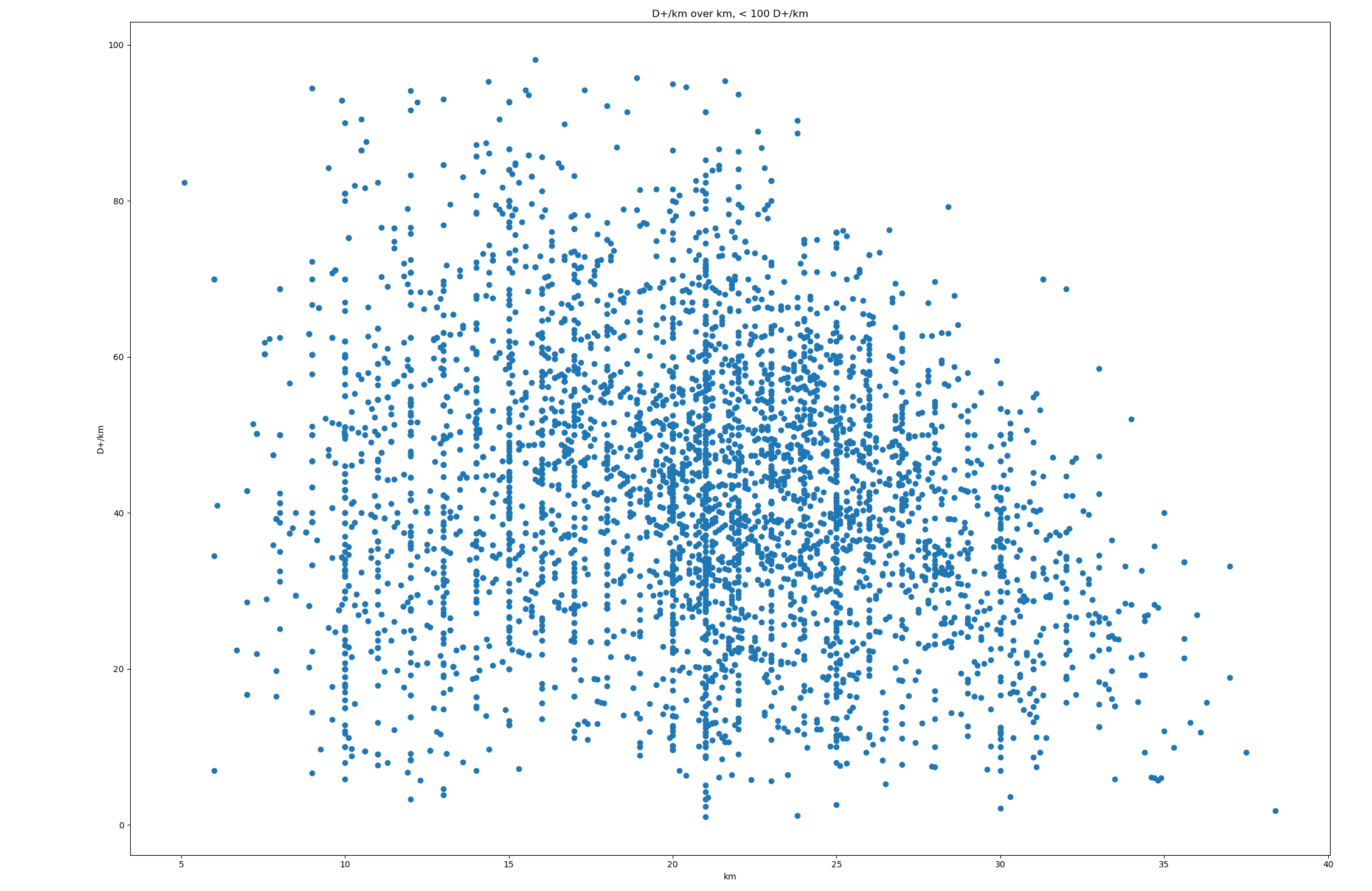
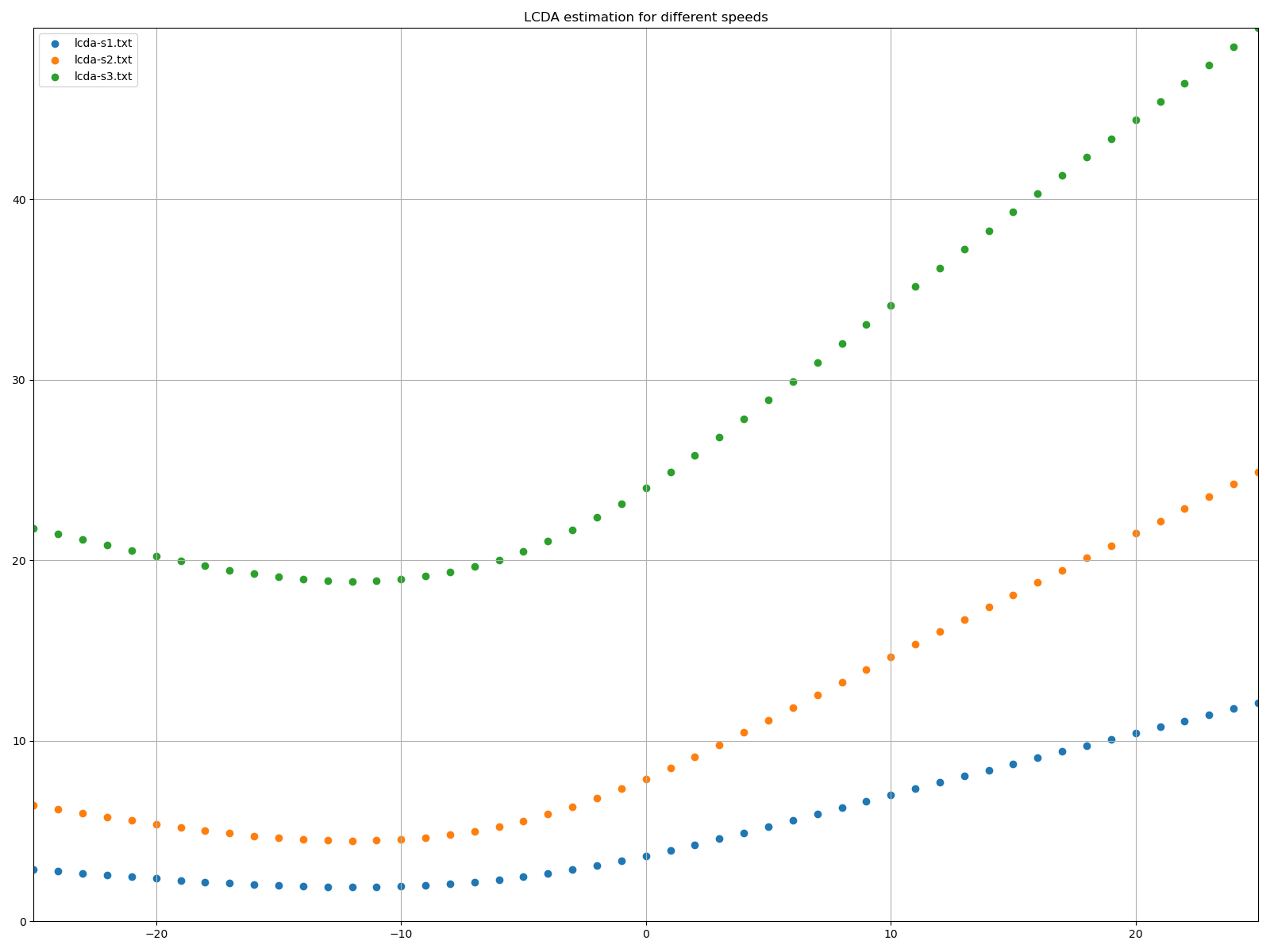
Le résultat obtenu est … 0.37. L’estimation serait donc que 100m de D+ équivaut à 370m.
Voici les 25411 courses que j’ai utilisé, avec km, D+ et t (heures), trié par D+. Je peux fournir plus de données et scripts au besoin. Deux bouts de Python pour jouer avec les données :
Afficher/Masquer le contenu masqué
De quoi charger les données dans la variable data comme au dessus :
data = []
with open('race-stats.txt') as f:
for line in f:
km, dplus, h = line.split()
km, dplus, h = float(km), float(dplus), float(h)
if h > 1 and h < 4:
data.append((km, dplus, h))
data = np.array(data)
Et une fonction pour dessiner un kme′ et son estimation avec matplotlib :
import matplotlib.pyplot as plt
def draw(x, y):
plt.figure()
plt.xlabel('h')
plt.ylabel('kme')
plt.scatter(x, y)
z = np.polyfit(x, y, 1)
p = np.poly1d(z)
plt.plot(x, p(x), "r--")
plt.title("y=%.6fx+%.6f" % (z[0],z[1]))
plt.show()
Remarques et questions :
-
Je ne sais pas réellement comment vérifier mon résultat. Je me dis que je pourrais appliquer ma formule et voir que ça donne un meilleur résultat que α=1 par exemple. Mais ça reviendrai à faire exactement la même chose !
-
Vous pensez à d’autres démarches potentielles ?
Je me dis par exemple qu’on pourrait par exemple mesurer la consommation d’énergie d’un corps humain pour des efforts qui incluent, ou non, du dénivelé. Ça a probablement déjà été fait (?). -
Est-ce que vous voyez des méthodes pour exploiter les données individuels de coureurs ? Ça permettrait de voir si α change en fonction du niveau ou l’expérience par exemple.
-
Votre ressenti de coureur ? :-)
Le mien : je trouve 0.37 plus réaliste que 1.0, mais je m’attendais à une valeur entre 0.5 et 0.7.
Merci, et bonne soirée !