- KFC,
Bonjour à tous,
Je voudrais aujourd'hui vous proposer un défi ou exercice.
La difficulté du problème est grande et il s'agit d'un problème ouvert, mais je pense qu'il s'agit simplement d'un bon challenge à différents niveaux.
Avant de présenter le problème, je souhaite introduire les problèmes d'optimisation multi-objectifs.
Mono-objectif version multi-objectif
Mono-objectif
Traditionellement lorsque l'on parle de problème d'optimisation, on parle de trouver le minimum (ou le maximum) d'une fonction $f : E \to F$ où $E$ est l'espace des variables de décision et $F$ généralement $\mathbb{R}$, appelé l'espace objectif.
On peut alors écrire ce problème $\underset{x \in F}{min} f(x)$, qui signifie « trouver $x$ appartenant à $F$ tel que $f$ atteigne son minimum en $x$ ».
Généralement on rajoute des contraintes $g_i$ sur l'espace $F$ et l'on réécrire le problème de la manière suivante:
$\underset{x \in F \\ g_i(x) \leq b_i}{min} f(x)$ que l'on peut lire « trouver $x$ appartenant à $F$ ET tel que $x$ satisfasse toutes les contraintes $g_i(x) \leq b_i$ tel que $f$ atteigne son minimum en $x$.
Tout problème de décision, par exemple « existe-il un nombre premier dont la somme de ses chiffres vaut 12345 ? » peut se mettre sous la forme de problème d'optimisation. De même, énormément de problème de la vie de tous les jours peuvent se mettre sous forme de problème d'optimisation comme « quel mettre en couple des personnes pour maximiser le bonheur de chacun ? », « quelle la stratégie optimale pour jouer au shifumi ? », etc.
On comprendra pourquoi c'est une branche des mathématiques très féconde en applications.
Contrairement à l'idée reçue, la difficulté d'un problème d'optimisation ne provient pas de sa classe, c'est à dire par exemple s'il est Polynomiale ou Non-déterministe Polynomial (NP-complet ou NP-dur)[^1], mais de la forme de l'espace contraint et de la forme de la fonction $f$. Les problèmes « faciles » sont les problèmes où ces éléments sont convexes. Les problèmes « difficiles » sont les problèmes où ces élements sont concaves. Le cas médian, où les contraintes sont linéaires, est généralement appelé programmation linéaire est également un problème facile (les méthodes des points intérieurs sont polynomiales sur les problèmes d'optimisation linéaire, quadratique convexe, semi-définie positive).
Enfin, ce genre de problèume peut ne pas admettre de solution (surcontraintes) ou une seule solution (il se peut que plusieurs points de $E$ donne la même valeur pour $f$ mais on parle ici de la valeur de $f$ minimale qui est unique).
Multi-objectifs
Dans la réalité, la plupart des situations sont multi-objectifs et l'on ne veut pas optimiser un seul objectif mais plusieurs à la fois : une entreprise qui fabrique un produit voudrait minimiser le coût de production du produit et maximiser sa qualité.
Un problème d'optimisation multi-objectif n'est donc pas très différent en apparence d'un problème mono-objectif dans sa formulation:
On notera que l'on a remplacé $min$ ou $max$ par $opt$ car il se peut que l'on veuille maximiser selon un objectif et minimiser selon un autre, comme décrit dans l'exemple ci-dessus. En réalité on peut toujours se ramener au cas de minimisation en disant que l'on ne cherche pas à maximiser la qualité mais minimiser les défauts par exemple et au lieu de maximiser $f_i$ on minimisera $-f_i$.
La question que vous devez vous poser est: en quoi est-ce différent par rapport à un problème mono-objectif ? Si dans un problème mono-objectif il était facile de déterminer l'optimilité d'une solution par rapport à une autre (si vous avez $x$ et $y$ deux solutions, si $f(x) < f(y)$ et que vous minimisez $f$, alors $x$ est meilleur que $y$), en multi-objectif la notion d'optimalité est modifiée.
En effet, imaginons que dans l'exemple de production donné donné plus haut (en cherchant à minimiser les deux objectifs pour simplifier), j'ai les solutions suivantes: $A = \begin{pmatrix}5\\10\end{pmatrix}$, $B= \begin{pmatrix} 6\\ 7 \end{pmatrix}$ et $C = \begin{pmatrix}12\\11\end{pmatrix}$
S'il est clair que $C$ est moins bon que $A$ et $B$ car ses deux composantes sont moins bonnes, comment comparer $A$ et $B$ ? En effet, $A$ est meilleur sur le premier objectif (le cout), mais présente plus de défauts, tandis que $B$ est coute plus cher mais présente moins de défauts. Les solutions $A$ et $B$ sont dites « non-comparable au sens de Pareto ». La solution $A$ « domine au sens de Pareto » la solution $C$, la solution $B$ domine la solution $C$ et la solution $C$ est dominé par $A$ et par $B$. Parmi tous les éléments de $E$, l'espace des variables de décisions, l'ensemble des élements qui ne sont pas dominés est appelé l'Ensemble de Pareto et les vecteur objectifs associés sont appelé le Front de Pareto.

Certains pourrait me dire qu'il est préférable de choisir $B$ car il ne coute qu'une unité de plus mais réduit de 3 unité les défauts par rapport à $A$. Ce à quoi je répondrais que le choix ne peut être fait qu'en présence du maximum d'information, c'est à dire le Front de Pareto complet.
En résumé, un problème multi-objectif ne présente pas une seule solution comme les problèmes mono-objectifs, mais un ensemble de solutions qui représente des compromis. Au décideur de prendre la décision final, lorsqu'il aura toutes les cartes en main pour décider, à savoir l'ensemble des éléments du Front de Pareto.
Le problème
Après ce vaste hors-sujet, je présente ici le problème à résoudre.
Il y a $n$ villes $C_i$, toutes reliées entre elles, formant ainsi une clique. Une ville de départ $C_I$ et une ville d'arrivée $C_G$ sont également reliées à toutes les villes centrales. $t$ passagers attendent en $C_I$ pour se rendre en $C_G$. $p$ avions sont initialement en $C_I$ et ne peuvent chacun transporter qu'une personne à chaque instant.
Chaque arc possède une durée $d_{ij}$ représentant le temps de vol entre la ville $C_i$ et $C_j$. Les durées sont symétriques, ce qui implique que $d_{ij} = d_{ji}$ (EDIT: ce n'est pas le cas de l'illustration ci-dessous). Aussi, se poser dans une ville $C_i$, à cause des droits de douane, coûte $c_i$ (à l'exception de $C_I$ et $C_G$ qui ont un coût nul.
Une solution faisable à ce problème est appelé un « plan ». Un plan décrit à chaque instance ce que fait chaque avion. Par exemple « il va à de $C_i$ à $C_j$ vide et prend le passager qui se trouvait en $C_j$ ». Le coût du plan est évidemment la somme de toutes les villes croisées au sein du plan (et donc quelque soit les avions). Cependant, la valeur du temps, que l'on appelle « makespan » dans le domaine de la planification, est la valeur maximale de l'exécution des actions d'un avion. En effet, chaque avion travaille en parallèle et donc la durée total pour finir d'amener les passagers est donné par le moment où le dernier avions termine sa séquence d'actions.
L'objectif est d'amener les $t$ passagers de $C_I$ en $C_G$ avec le makespan et le cout minimal.
Je ne donne pas plus de contraintes sur les distances $d_{ij}$ et les $c_i$ mais vous vous doutez bien que le cas intéressant est lorsque le cout augmente lorsque le temps diminue (sinon il n'y a pas de compromis à faire).
Voici une instance du problème (les villes $C_I$ et $C_G$ ont été appelé $C_0$ et $C_4$) avec $n=3$:
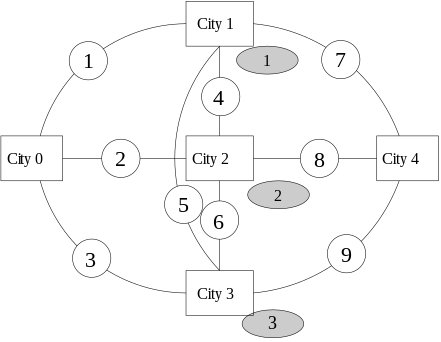
L'exercice
L'exercice consiste à trouver un algorithme qui donne l'ensemble du front de Pareto de problème. Il s'agit de donner le Front de Pareto et non nécessairement l'Ensemble de Pareto, c'est à dire qu'éventuellement, construire explicitement les plans n'est pas obligatoire.
L'algorithme doit être le plus efficace possible surtout donner l'ensemble des points du front. Il ne doit en manquer aucun.
L'algorithme doit prendre en entrée: $n$, $t$, $p$, le vecteur des couts et les distances. Cela permettra de comparer les algorithmes et implémentation sur une série de scripts en fonction des valeurs des entrées.
Si vous pouviez calculer la complexité dans le pire des cas de votre algorithme (eventuellement cas moyen et meilleur des cas), ainsi que prouver que la méthode fonctionne (si nécessaire), ça serait encore mieux !
Conseils:
- Exploitez au maximum les symétries présentent dans le problème.
- Ne vous inquietez pas si votre algorithme ne permet pas de résoudre en temps raisonnable même de petites instances. Le problème est PSPACE complet, disons grosso-modo, plus dur théoriquement que les problèmes NP-Complet.
- N'hésitez pas à poser des questions. Vu la complexité du problème et l'ensemble des notions sous-jacentes, il est fort probable que j'ai mal expliqué certaines choses.
[^1] : N'allez jamais dire qu'un problème est non polynomial, ou alors venez chercher votre prix de un million de dollars à l'Institut Clay.

