Salut,
Je viens soliciter votre aide, parce que j'ai un problème qui me chipote. Je dois analyser des molécules qui ont la forme d'une spirale (comme l'ADN, par exemple). Je sais qu'elles ont la forme d'une spirale et que donc, je peux les décrire, pour des unités répétitives (ou pour les coordonées du même atome qui se répète) en employant
Sauf qu'employer les coordonnées cylindriques requière que la spirale soit effectivement orientée selon un axe (Z dans ce cas-ci). Et là c'est le drame, puisque ce n'est absolument pas le cas (j'ai bien la spirale, mais elle est orientée n'importe comment). J'aimerai donc savoir si il existe un moyen simple et mathématique (que je sache implémenter dans un langage de programmation conventionnel) pour réorienter mes points de manière à ce que ma spirale soit dans le bon sens et que je puisse y appliquer ma formule ci-dessus ?
Sachant que mes recherches m'ont poussé à regarder si il n'y avais pas moyen de trouver la position du centre et de réorienter ensuite la molécule en calculant plusieurs fois le centre (en fait en cherchant l'équation du cercle correspondant avec 3 ou 4 points). Et ça ne fonctionne pas, parce que:
- si je prend juste la coordonnée $x$ et $y$ (comme l'équation de la spirale le laisse entendre, puisque $z$ peut s'obtenir à partir de $x$ et $y$), comme tout est orienté n'importe comment, ça ne fonctionne pas (ça fonctionnerai si la molécule était déjà aligné selon un axe)
- Si je prend $x$, $y$ et $z$, j'ai un centre, mais qui ne correspont pas au "bon centre", puisqu'il s'agit non pas d'un cercle mais d'une spirale, et je suis coincé.
Donc si quelqu'un avait une proposition, j'avoue que ça m'aiderai 
D'avance merci.

 :
: 



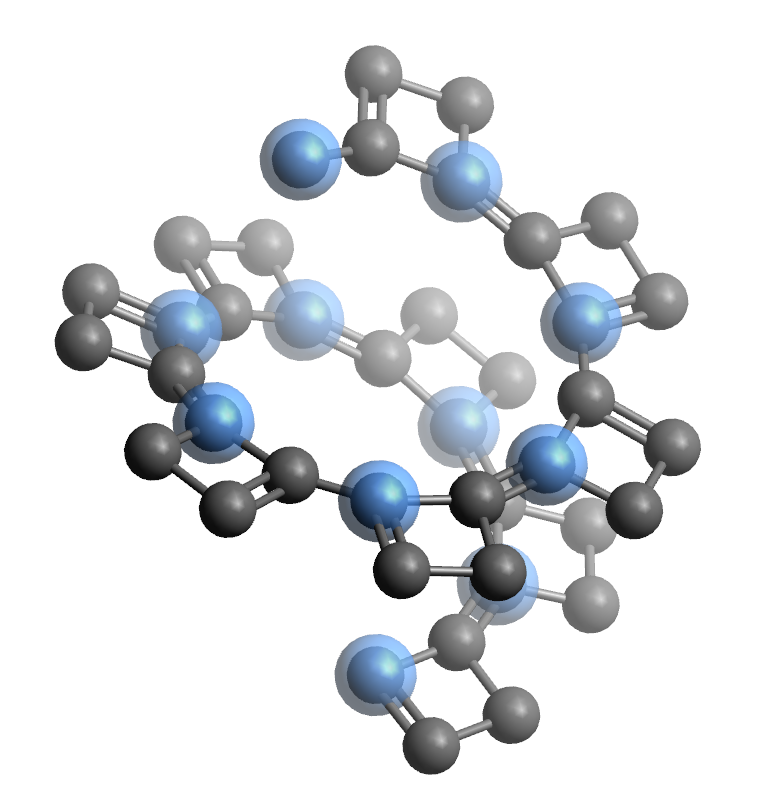

 (En fait je ne connais pas la différence entre Hélocoïdale et Hélice, c'est peut-être là que j'suis dans l'flou ^^' )
(En fait je ne connais pas la différence entre Hélocoïdale et Hélice, c'est peut-être là que j'suis dans l'flou ^^' )