Salut à tous.
Je suis débutant en électronique et j'ai trouvé un cours intéressant sur les portes logiques : http://www.ai.univ-paris8.fr/~audibert/ens/6-PORTESLOGIQUES.pdf. J'ai fais les quelques exercices de la partie 6 que voici :
Considérer un porte ET à quatre entrées. Elle ramène 1 lorsque les quatre entrées valent 1, et 0 sinon.
1) En utilisant l’associativité abcd = ((ab)c)d, faire le schéma de cette porte en utilisant uniquement des portes ET à deux entrées.
2) En utilisant l’associativité : abcd = (ab)(cd) faire le schéma de cette porte en utilisant uniquement des portes ET à deux entrées.
3) En utilisant le fait que abcd = $\overline{\overline{(ab)(cd)}}$ et en utilisant une loi de Morgan, montrer que la porte ET à quatre entrées peut être construite avec deux portes NON ET et une porte NON OU, et faire le schéma.
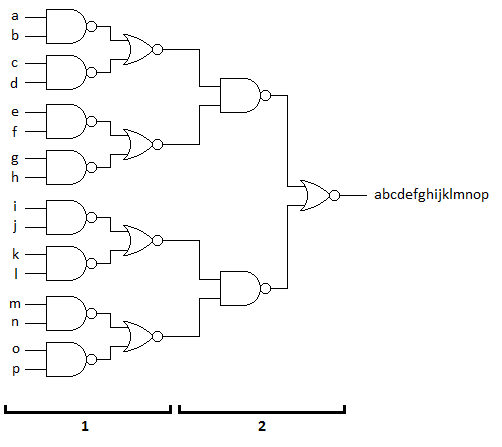
4) Généralisation : En reprenant le procédé du 3), faire le schéma d’une porte ET à 16 entrées en utilisant des portes NON ET et NON OU.
J'ai pas eu trop de problème pour les 3 premières questions mais pour la quatrième je bloque (et il n'y a pas le corrigé). Est-ce que quelqu'un pourrait me mettre sur la voie ?
Aussi, voici mes réponses. Je ne me suis pas trompé ?
1) Schéma de ((ab)c)d :
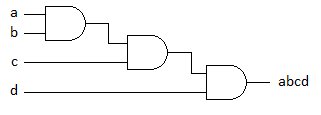
2) Schéma de (ab)(cd) :
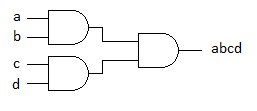
3) $abcd = \overline{\overline{(ab)(cd)}} = \overline{\overline{(ab)}+\overline{(cd)}}$
Schéma :
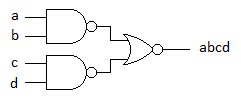
Merci d'avance.


 !
!