Bonjour !
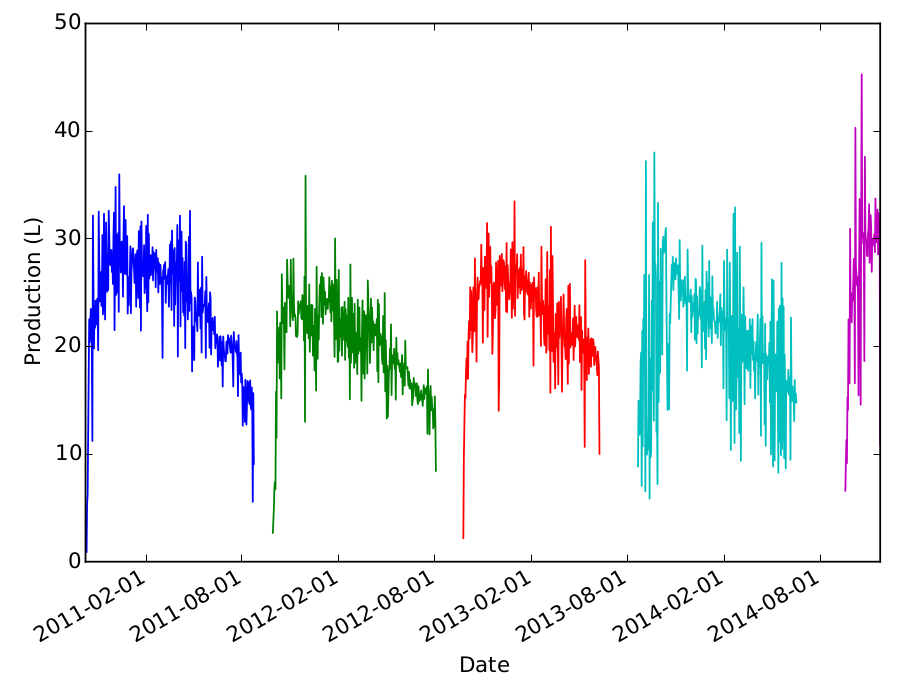
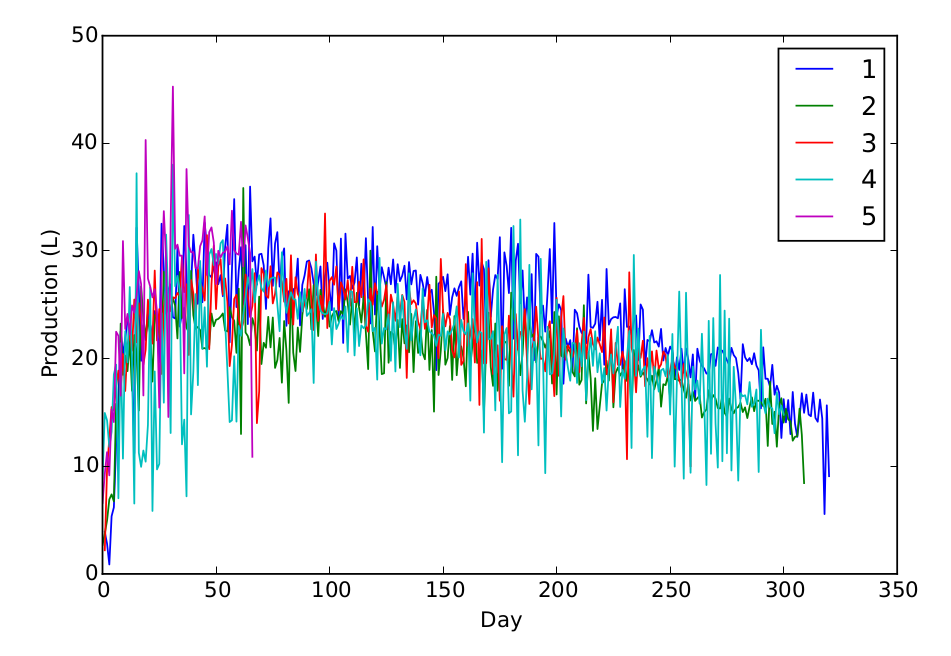
Page 29 de ce PDF, il est indiqué que l'étude de la suite $(x_{t} - x_{t-1})$ constituait un moyen simple pour déterminer la tendance de la série temporelle.
Peut-être ne comprené-je, mais je ne vois pas comment ça peut fonctionner quand il y a des variations. Faire la différence donne la pente pour une droite (en considérant les abscisses écartées d'une unité), mais pas du tout pour un cosinus par exemple (la tendance serait une droite horizontale).
Edit : Page 30, il est question de seasonal differencing :
For example, with monthly data, where there are 12 observations per year, the seasonal difference is written as ∇{12}x{t} = (x_{t} − x_{t-12}).
Cela ne permet-il pas aussi de déterminer la tendance ?
Merci.
+0
-0