Bonjour,
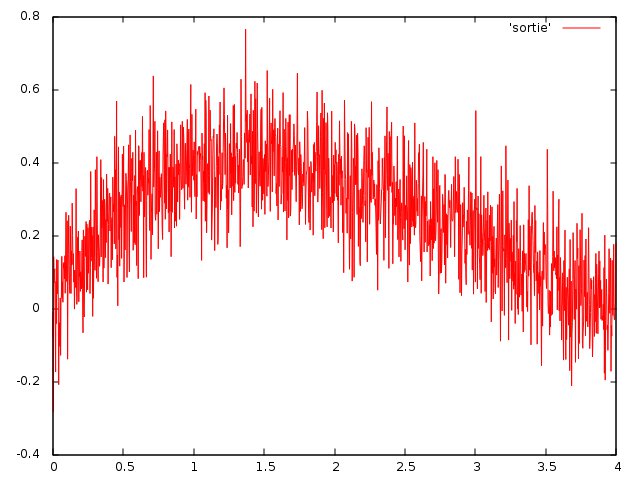
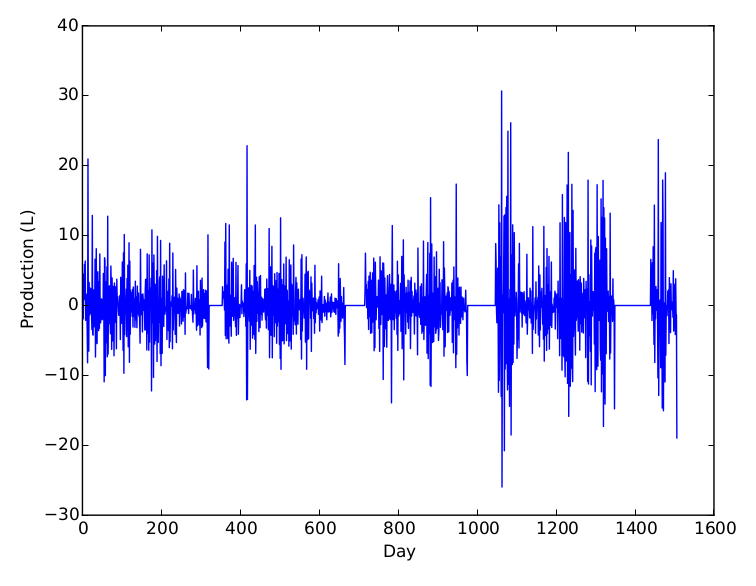
J'utilise la bibliothèque statsmodels (Python) et je travaille sur ces données (chez moi, les graphes ne s'affichent pas sur GitHub).
Conformément à cet exemple, je génère un modèle :
1 2 3 4 5 6 | import statsmodels.api as sm p = 1 d = 0 q = 1 model = sm.tsa.ARIMA(data, (p, d, q)).fit() |
Puis, en m'inspirant de ça, je crée un processus :
1 | process = sm.tsa.ArmaProcess(model.arparams, model.maparams) |
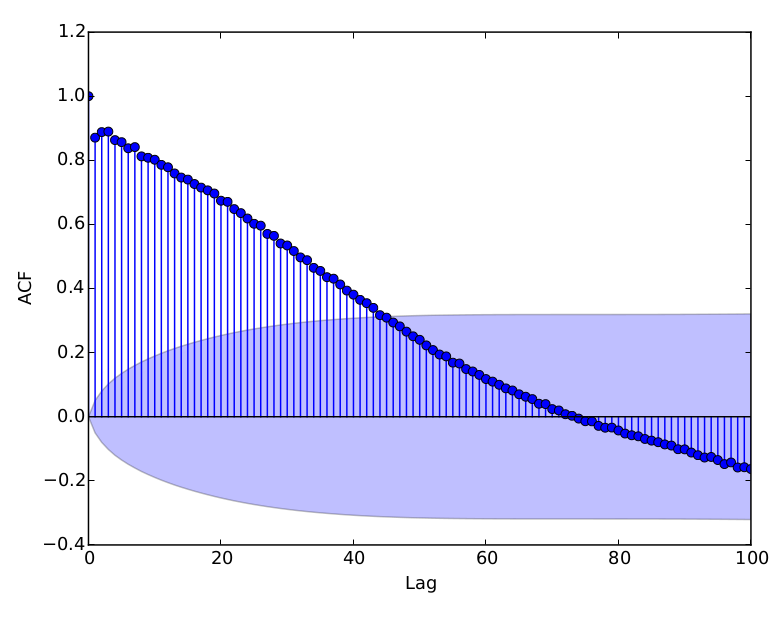
Or l'ACF et la PACF montrent assez clairement qu'il n'est pas stationnaire. Pourtant :
1 2 3 4 | >>> process.isinvertible True >>> process.isstationary True |
Et, mais ça semble plus cohérent, on retrouve le même résultat (sauf au niveau des paramètres AR et MA) après une différenciation.
Ai-je mal compris quelque chose ou y a-t-il un problème au niveau de la lib ?
Merci !
+0
-0



 Ton phénomène n'est pas stationnaire (mais peut-être périodique), ton modèle est stationnaire. Soit il y a une erreur quelque part (interprétation, calcul…), soit le modèle ne décrit pas correctement les données. Je ne trancherai pas…
Ton phénomène n'est pas stationnaire (mais peut-être périodique), ton modèle est stationnaire. Soit il y a une erreur quelque part (interprétation, calcul…), soit le modèle ne décrit pas correctement les données. Je ne trancherai pas…