Hexagonal Compact - Compacité

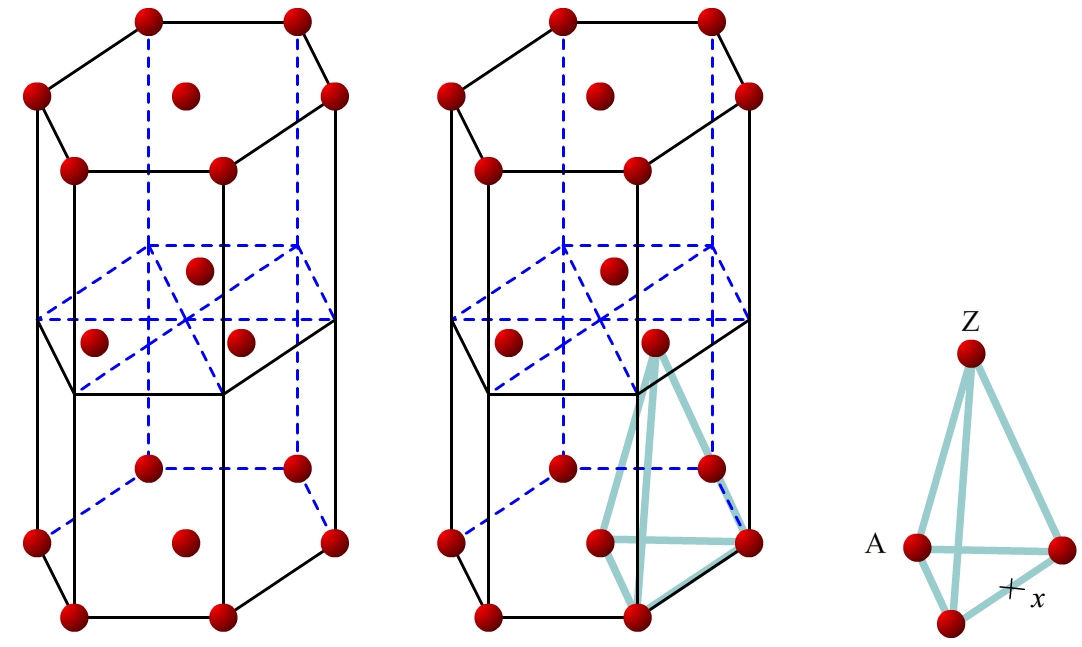
Bonsoir, j'ai appris en cours que pour calculer la compacité d'une structure cristalline, je devais isoler le plan pour lequel il y a le plus d'atomes, puis chercher la distance qui sépare les 2 atomes les plus éloignés. ça marche globalement bien (des précisions ici : http://eduscol.education.fr/rnchimie/chi_gen/dossiers/kh/01_structure_cristalline.pdf)

Sauf pour l’hexagonal compact où je n'y arrive pas du tout .. Je n'ai pas compris la méthode. J'ai trouvé une expression de ce genre mais je n'arrive pas à la redémontrer :

Je veux juste qu'on m'explique comment le redémontrer simplement

Merci

Habituellement la méthode que j'emploi c'est un rapport : volume de sphère multiplié par le nombre d'atome par maille. le tout divisé donc par l'espace de la maille.

Le volume d'une sphère est certes réducteur, mais est simple à calculer. Ensuite le nombre d'atome par maille en structure hexago c'est 6 ?

Puis le volume de maille se mesure avec la hauteur de la maille multiplié par la surface d'un hexagone, géométrie basique ? non ?

La formule que j'emploi habituellement c'est le nombre d'atome par maille multiplié par la volume de la sphère le tout divisé par a au cube.

Je suis d'accord que le nombre d'atome par maille est 6. Mais comment trouver r en fonction de a ?

Bah $\mathrm{a}$ c'est le parametre d'un cube. Mais dans le cas d'une maille hexagonal tu dois un peu réfléchir en géométrie !

Avec $\mathrm{S}$ surface de l'hexagone. Un hexagone, c'est 6 triangle équilatéraux, j'espère que tu sais trouver la surface d'un triangle équilatéral ???

$\mathrm{S = 6s}$ Avec $\mathrm{s}$ surface d'un petit triangle.

Pour la hauteur $\mathrm{H}$ c'est un peu compliqué, j'te conseille de regarder ce post.

PS : désolé si je ne suis pas claire, demain je te ferais une réponse clair et précise si tu veux, mais là j'suis KO Demain j'te photographie des pages que j'ai redigées.

Je veux bien que tu m'expliques plus clairement demain si possible

Je sais que ce sont des relations géométriques simples mais j'ai pas réussi à trouver la méthode générale. Sur les CC ou les CFC j'ai réussi à comprendre la méthode (c'était la même) mais là, j'aimerai étendre cette méthode aux HC. Si tu pouvais me le détailler demain, je veux bien

Merci

Très clair merci !

lol j'ai écris "triangle rectancle"

bonjour, stp comment calculer les parametres de maille (a, b et c) pour une structure hexagonale

Salut,

De quelles infos disposes-tu ?

Qu'as-tu essayé de faire ?

Je te conseille de lire ce que j'ai publié plus haut car cela est clairement en rapport avec les paramètres d'une maille hexagonale.

BONUS introductif

Salut,

il faudrait préciser un peu ce que tu entends par là. Les paramètres de maille ne sont pas définis que par la structure, mais aussi par les conditions physiques (P, T, B…) et les atomes présents.

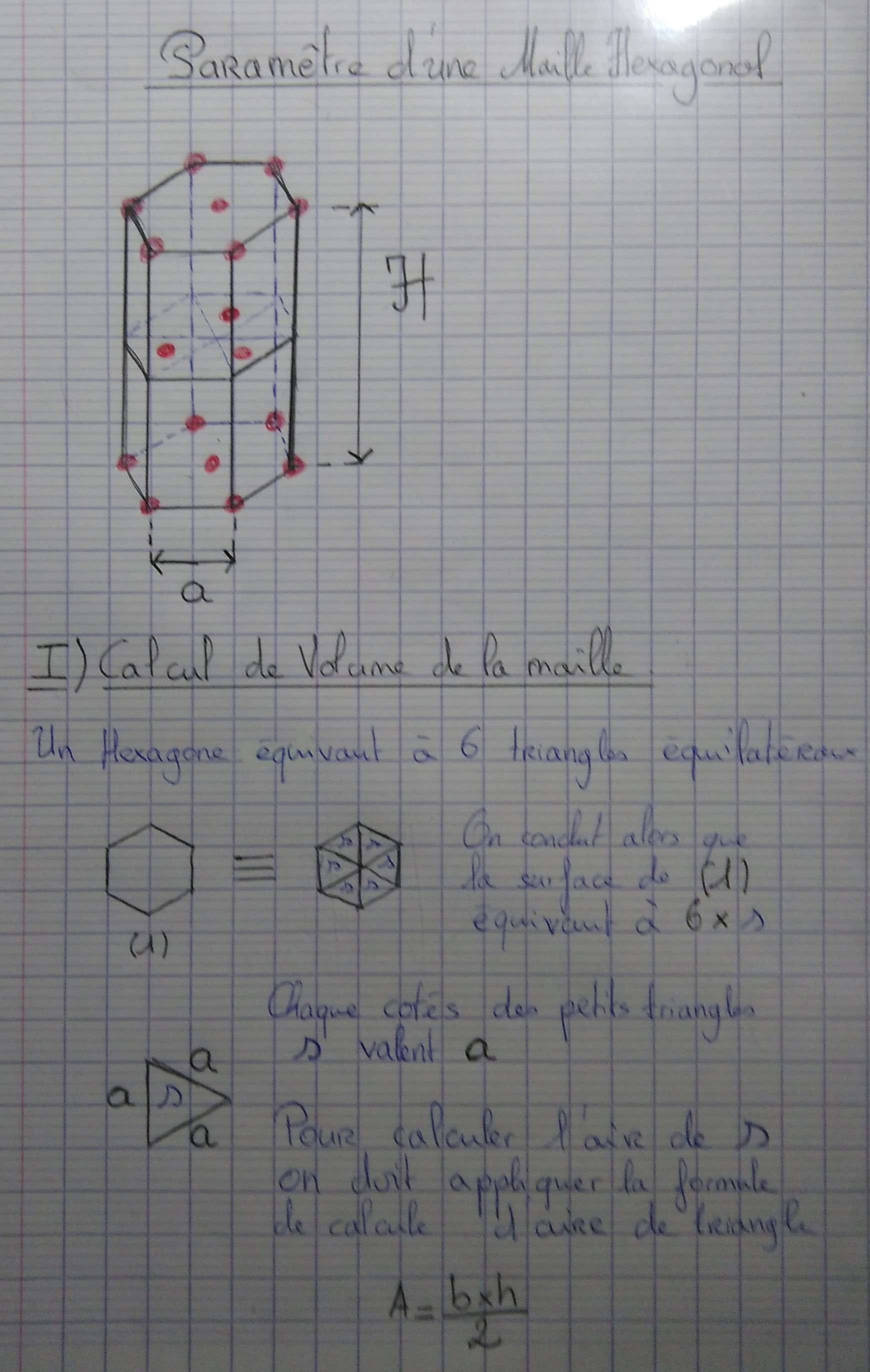
Il est possible de calculer numériquement les paramètres de mailles (et bien plus ) à partir des conditions physiques et les atomes présents en utilisant des ordis pour résoudre des versions simplifiées de l'équation de Schrödinger, mais je doute que ce soit ce que tu attends comme réponse…

À moins que tu ne soit spécialisé en mécanique quantique et/ou chimie computationnelle, on ne te demandera probablement jamais ce genre de trucs et les paramètres de mailles seront données dans l'énoncé ou on te donnera un jeu de données expérimentales (typiquement diffraction à rayons X) qui te permettront de remonter facilement aux paramètres de maille du réseau étudié (loi de Bragg par exemple).

Il est difficile de t'en dire plus sans avoir un contexte autour de ta question.

Par ailleurs, quand tu as une question, il vaut mieux à l'avenir créer un nouveau sujet plutôt que de répondre à la fin d'un autre sujet.

je fait l'étude de DRX de l'alliage CaNi5 et j'ai l'analisé par le logiciel X'pert high score qui ma donne les pic et le distance reticulaire de chaque pic. le proble ce comment je doit calculer a et c apartir de loi de Bragg

Je te conseille d'ouvrir un nouveau poste alors Avec tes resultats directement pour qu'on puisse t'aider.

ou est la troisieme page ?

Les images étaient trop lourds pour être uploadé sur le site zestedesavoir.com directement. Donc les liens sont brisés.

La page trois concerne la hauteur d’un tétraèdre :

$x$ est un point qui se trouve au milieu du coté d’un tetraèdre.

@Aaron Tshilumba

Merci de ne pas déterrer des sujets et de créer un sujet propre. Par ailleurs, il convient de bien introduire son sujet et de montrer que tu as cherché la réponse.