(novembre 2015) Simulation d'un feu de forêt

a marqué ce sujet comme résolu.

Salut,

Alors, pour ma part j'avais deux heures à perdre du coup voici le début d'une ébauche:

  • Génération d'un polygone aléatoire qui consiste à générer des points autour d'un centre. Le point suivant est généré par un angle par rapport au précédent et une longueur. Les deux grandeurs sont tirées suivant une loi normale, et les paramètres de variance et de moyenne permettent de gérer la régularité et la rotondité du polygone.
  • Comme le polygone n'est pas forcément très joli, on le lisser via l'algorithme itératif de Chaïkin, qui s'apparente à une régularisation via des Splines. Une ou deux passes sont suffisantes, surtout que chaque passe multiplie par deux le nombre de faces du polygone.

Ces deux premières étapes permettent d'obtenir une zone pour une forêt qui semble réaliste.

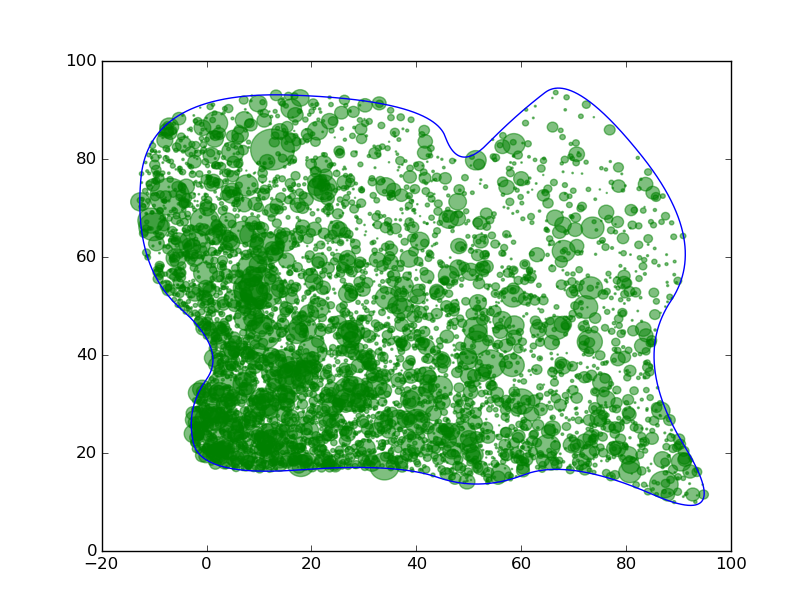
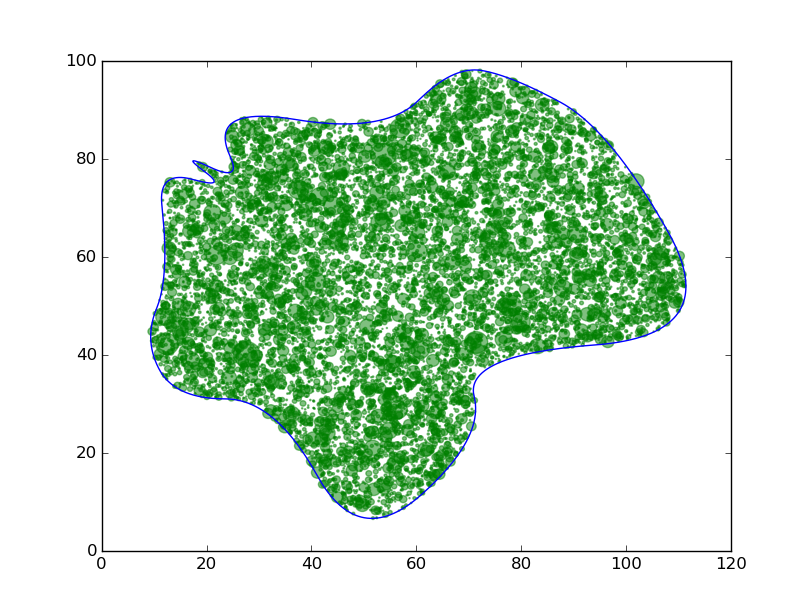
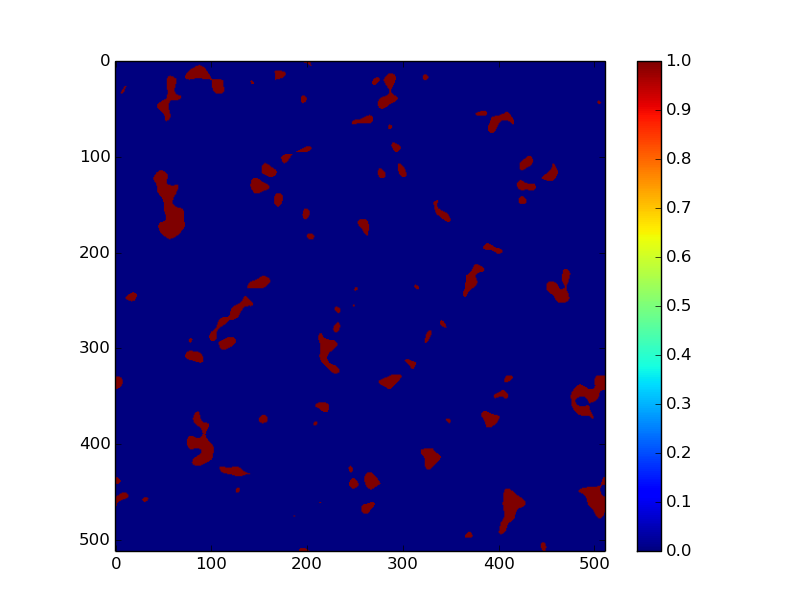
Ensuite, on générer des arbres aléatoirement dans cette zone et selon une distribution de probabilité particulière. Pour cela, on utilise la méthode de rejet pour générer des points à l'intérieur de notre polygone uniquement, et la méthode d'inverse généralisée pour simuler une distribution particulière (sur l'image suivante, selon l'axe x on a une loi normale et selon l'axe y une distribution exponentielle).

Pour le feu, ce qui nous intéresse c'est la "zone d'influence" de l'arbre, c'est à dire la zone dans laquelle tout autre arbre est susceptible de brûler. Sans vent, on peut admettre que globalement cette zone correspond au feuillage, qu'on peut approximer par un disque. Comme le rayon du feuillage est plus ou moins proportionnel à l'age de l'arbre, on modélisera le rayon d'influence par une loi exponentiel. Du coup, pour chaque arbre, on tire aléatoirement un rayon selon cette loi.

Pour chaque arbre on calcul le graphe de recouvrement, c'est à dire que si deux arbres ont une zone d'influence qui s'entrecoupe, on les relie.

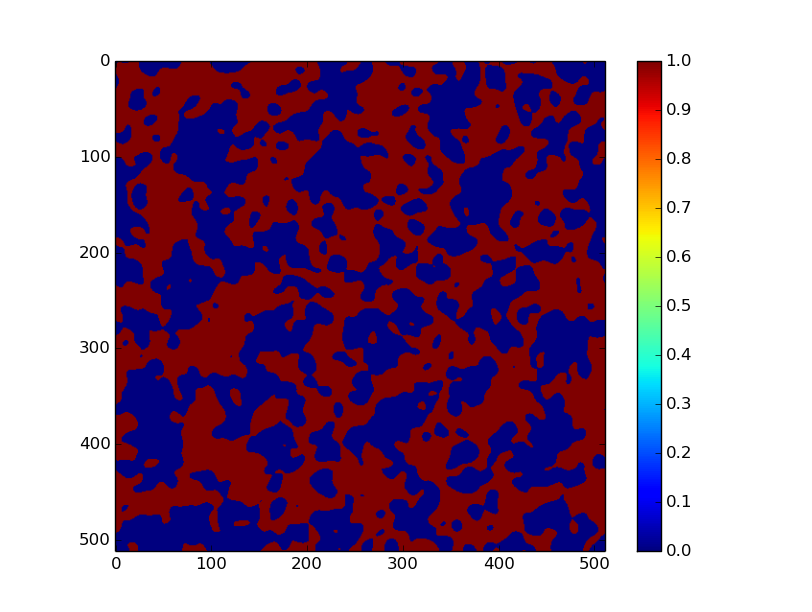
Bon, comme tout à été tiré aléatoirement jusqu'à présent, on considère arbitrairement que le premier arbre de notre liste à décidé de faire une auto-combustion. De cet arbre, grâce à un algorithme de parcours tout simple, on marque comme brûlé les arbres de voisins en voisin.

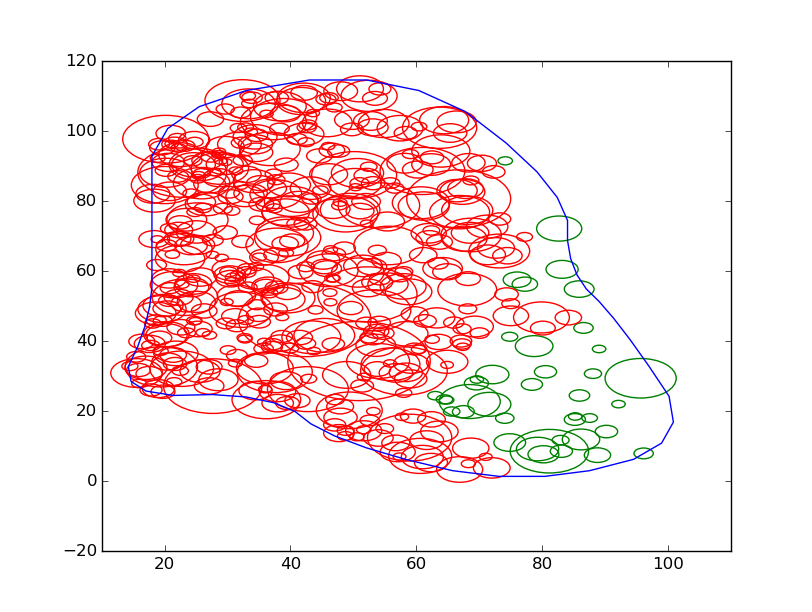
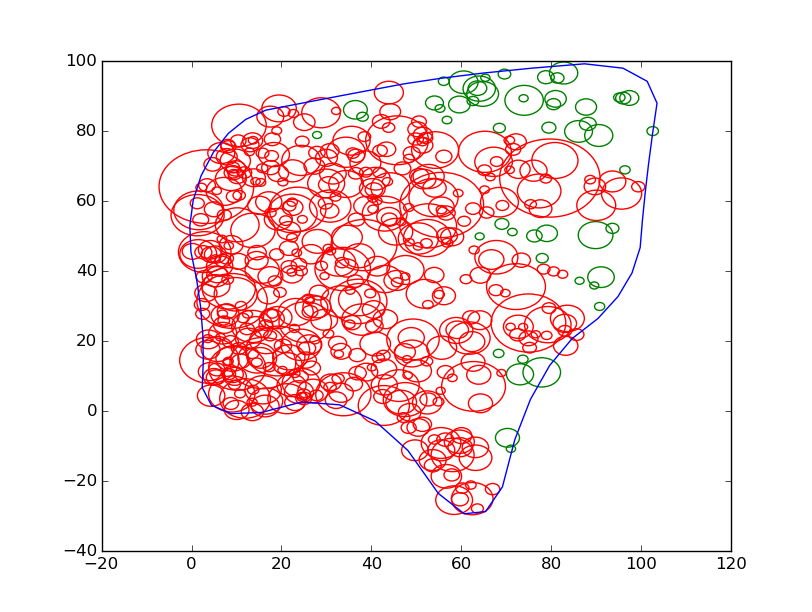
Un résultat Un autre

Comme on peut s'y attendre, les arbres non brûlés sont situés à droite puisqu'il y a une densité plus faible à droite qu'à gauche à cause de la densité exponentielle.

Forêt générée selon deux lois exponentielles. Forêt générée selon deux loi uniformes.

Amélioration à venir :

  • Intégrer les statistiques sur les arbres brûlés et non brûlés.
  • intégration du vent : le vent déforme les cercles d'influence en ellipses d'influence selon le sens du vent et le rayon initial.
  • la zone d'influence est un gradient orienté vers l'extérieur.
  • la zone d'influence est probabiliste : en fonction de la distance centre à centre, et des ratios de surfaces on a pas la même probabilité de brûler, à voir.
  • une version 'temporelle', où l'on peut voir le résultat au fur et à mesure.
  • une version 'physique' où l'on a une diffusion de la chaleur dynamique (c'est facile à faire sur une zone d'influence, par contre aux interfaces et en cas de superposition, ça pue…)
+9 -0

Voici ma participation un peu tardive.

Puisque personne ne l'a fait en java, et pour m'exercer sur des principes de POO, je l'ai fait dans ce dernier.

Mon programme sait faire la simulation et l'afficher en temps réel. Il enregistre l'image final. Bref, rien de plus que les autres participants pour le moment.
En revanche, je ne calcul pas encore les chiffres des résultats pourtant demandé à la base. Mais cela ne va plus être très dur à implémenter.

Voilà le code source.

+0 -0

Salut,

Je me permet de poster des résultats d'un autre problème où l'on peut étudier la percolation : celui du contact d'une surface rugueuse rigide sur un solide élastique à surface plane. On utilise généralement une surface rugueuse fractale, ce qui génère des zones de contact réparties sur la surface. Quand on accroit la charge appliquée, le nombre et la taille des zones de contact augmentent. Pour des charges élevées, certaines zones fusionnent avec d'autres pour donner des zones plus larges. Au bout d'un moment, la percolation entre les zones de contact se produit.

Contact clusters - load 0.02

Contact clusters - load 0.3

Et pour montrer la transition, voici un graphe du nombre de zones dont la taille est supérieure à une limite fixée en fonction de la charge appliquée.

Contact clusters - limit

C'est pas du feu de forêt, mais je pense que ça méritait quand même une petite mention :) . Je peux donner des références si vous voulez explorer un peu le sujet.

+6 -0

Et pour montrer la transition, voici un graphe du nombre de zones dont la taille est supérieure à une limite fixée en fonction de la charge appliquée.

C'est marrant, je m'attendrais à le voir plutôt tendre vers 1. Enfin, plutôt augmenter dans un premier temps, puis dégringoler quand l'effet de fusion se met en place, comme sur ta deuxième figure où il y a une seule grosse zone rouge, et une quinzaine de petites tâches minuscules. Il y a un truc que j'ai mal compris ?

+0 -0

La surface est fractale, donc il y a toujours de nouveaux clusters qui sont créés quand on augmente la charge. De plus la charge est trop faible pour avoir un contact total (dans ce cas le nombre de clusters tomberait à 1). Mais c'est un phénomène qui découle aussi du comportement des matériaux. Quand on inclut de la plasticité par exemple, on a une grosse localisation des clusters (cf. cet article).

+0 -0

Voici donc une autre version en Python pour la simulation de feu de forêt. Ce n'est pas la solution la plus optimisée, notamment tour_de_chauffe(…), mais ça doit être assez compréhensible. Pour changer de simulation, il faut modifier les deux premières constantes (TAILLE_FORET et PROBABILITE)

Je me suis posé la question si les voisins des diagonales étaient aussi impactés, mais apparemment non vu ce qu'ont fait les autres zesteux. ^^

Le code :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
from random import *

''' Programme de simulation d'un feu de forêt d'après le défi de Zeste de Savoir
https://zestedesavoir.com/forums/sujet/4690/novembre-2015-simulation-dun-feu-de-foret/ '''

'''Constantes'''
TAILLE_FORET = 50 #Modifier pour changer de simulation
PROBABILITE = 0.6 #Modifier pour changer de simulation
ARBRE_NORMAL = 0
ARBRE_EN_FEU = 1
CENDRES = 2

'''Fonction pour initialiser la liste contenant les arbres de la forêt'''
def initialise_foret():
    foret = [[ARBRE_NORMAL for colonne in range(TAILLE_FORET)] for ligne in range(TAILLE_FORET)]
    return foret

'''Fonction pour afficher le contenu de la forêt'''
def afficher_foret(foret):
    if TAILLE_FORET <= 50:
        str_ligne = '|'
        for ligne in foret:
            for emplacement in ligne:
                str_ligne = str_ligne + str(emplacement) + "|"
            print(str_ligne)
            str_ligne = '|'
        print("\n")

'''Fonction pour choisir un arbre aléatoirement pour le départ de feu'''
def depart_de_feu(foret):
    foret[randint(1, TAILLE_FORET-2)][randint(1, TAILLE_FORET-2)] = ARBRE_EN_FEU

'''Fonction qui retourne si l'arbre va brûler ou non à ce tour'''
def va_bruler(arbre):
    if arbre != CENDRES:
        if random() < PROBABILITE:
            return True
    return False

'''Fonction pour mettre en feu autour d'un arbre en feu'''
def allumer_le_feu(foret, pos_arbre):
    if pos_arbre[0]-1 >= 0 and va_bruler(foret[pos_arbre[0]-1][pos_arbre[1]]):
        foret[pos_arbre[0]-1][pos_arbre[1]] = ARBRE_EN_FEU
    if pos_arbre[0]+1 < TAILLE_FORET and va_bruler(foret[pos_arbre[0]+1][pos_arbre[1]]):
        foret[pos_arbre[0]+1][pos_arbre[1]] = ARBRE_EN_FEU
    if pos_arbre[1]-1 >=0 and va_bruler(foret[pos_arbre[0]][pos_arbre[1]-1]):
        foret[pos_arbre[0]][pos_arbre[1]-1] = ARBRE_EN_FEU
    if pos_arbre[1]+1 < TAILLE_FORET and va_bruler(foret[pos_arbre[0]][pos_arbre[1]+1]):
        foret[pos_arbre[0]][pos_arbre[1]+1] = ARBRE_EN_FEU

'''Fonction pour simuler un tour'''
def tour_de_chauffe(foret):
    arbres_en_feu = []
    for index_lig in range(TAILLE_FORET):
        for index_col in range(TAILLE_FORET):
            if foret[index_lig][index_col] == ARBRE_EN_FEU:
                arbres_en_feu.append((index_lig, index_col))
                foret[index_lig][index_col] = CENDRES
    for pos_arbre in arbres_en_feu:
        allumer_le_feu(foret, pos_arbre)
    for ligne in foret:
        if ligne.count(ARBRE_EN_FEU) > 0:
            return True
    return False

'''Fonction pour afficher le bilan final'''
def affiche_bilan(foret, nb_tours):
    totaux = [0,0,0]
    for ligne in foret:
        totaux[ARBRE_NORMAL] += ligne.count(ARBRE_NORMAL)
        totaux[ARBRE_EN_FEU] += ligne.count(ARBRE_EN_FEU)
        totaux[CENDRES] += ligne.count(CENDRES)
    print("- Fin de la simulation - ")
    print("Nombre de tours : "+str(nb_tours))
    print("Nombre initial d'arbres : "+str(TAILLE_FORET**2))
    print("Nombre d'arbres normaux : "+str(totaux[ARBRE_NORMAL])+" ("+str(totaux[ARBRE_NORMAL]/TAILLE_FORET**2*100)+"%)")
    print("Nombre d'arbres en feu : "+str(totaux[ARBRE_EN_FEU])+" ("+str(totaux[ARBRE_EN_FEU]/TAILLE_FORET**2*100)+"%)")
    print("Nombre d'arbres partis en cendres : "+str(totaux[CENDRES])+" ("+str(totaux[CENDRES]/TAILLE_FORET**2*100)+"%)\n")
    
if __name__ == '__main__':
    nb_tours = 0
    foret = initialise_foret()
    depart_de_feu(foret)
    afficher_foret(foret)
    while True:
        nb_tours += 1
        if not tour_de_chauffe(foret): 
            break
    afficher_foret(foret)
    affiche_bilan(foret, nb_tours)

+0 -0

Salut, La simulation des feux de forêt par automate cellulaire probabiliste était le "sujet" de mon TIPE. J’ai fait beaucoup (vraiment) de fonctions d’analyse, j’y ai également implémenté le vent avec la direction de 2 manières mais je ne suis toujours pas satisfait de mes 2 modèles (anisotropes). De plus, bien que les instructions dans les fonctions me semblent assez optimisés (utilisation maximale de numpy), la structure du code est pas belle (même si j’ai trié les fonctions dans différents fichiers) et j’ai pas mal de surcharges en quelque sorte. Il faudrait que j' "universalise" certaines fonctions pour simplifier le tout mais ma connaissance en Python reste limitée. De plus, je ne connaissais aucun autre modèle (que numpy et matplotlib), j’ai utilisé tkinter en traçant des carrés pour représenter les pixels (quelle honte…). Comme je suis en train d’apprendre le C++, je pourrai refaire quelques fonctions avec une bien meilleure interface graphique, mais c’est pas pour demain.

PS : J’ai eu 17,2/20 à l’épreuve.

Je n’avais pas connaissance de cette discussion lors de mon TIPE et je le découvre aujourd’hui. Quel dommage.

+0 -0
Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte