(Janvier 2016) Génération automatique de texte

Bonjour à tous.

Le défi de ce mois va s’intéresser à la génération automatique de texte.

Texte, langages et génération automatique

La définition tant attendue :

Le premier élément important à définir est la langue dans laquelle on va travailler.

Certaines langues sont dites vivantes (Par exemple, le Français, l'Italien, l'Anglais), d'autres sont dites anciennes (on ne les parle plus au jours le jours mais on les comprends, latin et grec ancien sont de bons exemples). Certaines sont qualifiées de mortes si on les comprends même pas (linéaire A, par exemple). Il existe selon les estimations entre 3000 et 6000 langues dans le monde.

Une langue va fixer :

• L'alphabet qu'on va utiliser. L'alphabet est l'ensemble des symboles qu'on va utiliser pour parler et écrire la langue : ce sont les lettres. La plupart des pays occidentaux utilisent l'alphabet Latin mais il en existe beaucoup d'autres, l'alphabet grec (chez nos amis grecs), cyrillique (utilisé en Russie et pays slaves) ou encore arabe.
• Le lexique c'est à dire l'ensemble des mots admissibles pour une langue donnée. Une bonne référence sur le lexique d'une langue est un dictionnaire de la langue incriminée.

A chaque mot est associé :

• Une catégorie : nom, verbe, adverbe, adjectif… Ces catégories servent lorsque la grammaire de la langue rentre en jeu
• Un ou plusieurs sens. Par exemple chat peut être un animal, mais aussi une conversation en ligne.

Enfin, la grammaire est un ensemble de règles qui servent à modifier les mots en fonction du sens qu'on veut donner à la phrase. Une règle de grammaire française est par exemple : Les verbes du 1er groupe se conjuguent en -ent à la 3eme personne du pluriel.

Maintenant que nous avons révisé nos cours de langue, nous pouvons nous pencher sur le sujet en lui même !

Génération automatique de charabia dans une langue donnée

Thématiques abordées : probabilité et génération aléatoire, unicode, GUI

Un point intéressant que la linguistique nous apprend est que la fréquence d’apparition des lettres va varier d'une langue à une autre, et ce même à alphabet constant.

Prenons l'exemple de l'anglais et du français. Les histogrammes d’apparition sont les suivant :

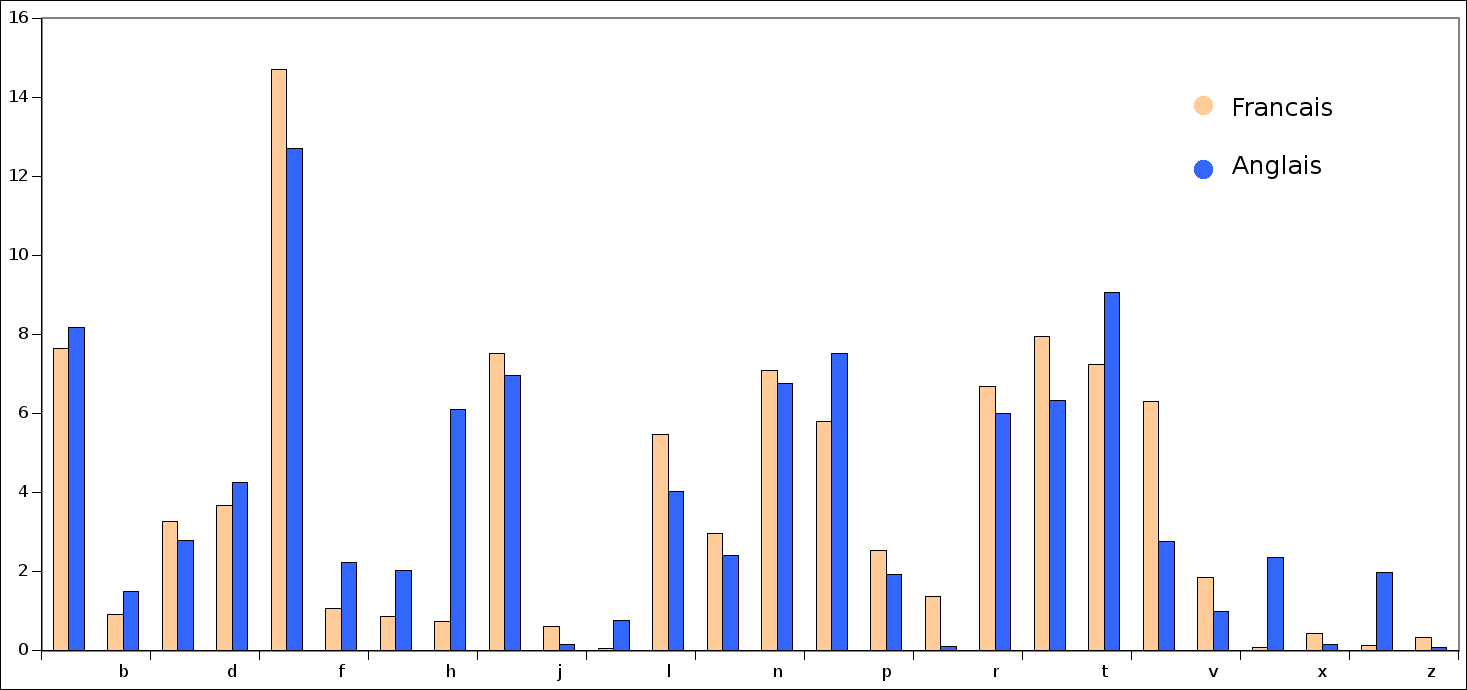
Le but de cette section du défi va être de générer une suite de caractères (autrement dit, du charabia) dans une langue donnée (ie suivant une distribution donnée). Vous trouverez les distributions pour différentes langues dans ce fichier CSV.

La génération demande de supporter des caractères plus variés que ce qu'on peut manipuler au jour le jour. La solution retenue pour gérer ce genre de chose s'appelle Unicode (ou UTF).

Pour réaliser ce petit générateur de charabia, les différentes étapes élémentaires sont :

• Afficher des caractères unicodes dans votre programme
• Lire des caractères unicodes depuis un fichier
• Lire un fichier CSV
• Tirer des nombres aléatoire en fonction d'une distribution donnée

Si vous avez réussi toutes ces étapes, il n'y a plus qu'à assembler ! D'ailleurs, une fois que votre générateur de charabia marche, pourquoi ne pas ajouter un mode quiz afin de deviner de quelle langue il s'agit et système de score persistant pour en faire un mini jeu ?

La distribution des fréquences se trouve ici

Génération de phrases par dictionnaire

Thématique abordée : fichier, génération aléatoire

Génération simple

On vous l'a sûrement dit à l'école, une phrase affirmative c'est sujet + verbe + compléments

Et bien on peut utiliser cette méthode pour générer des phrases. Si vous disposez d'une liste de sujets potentiels, de verbes et de compléments, alors en tirant au sort un de chaque vous pouvez générer une phrase.

Exemple :

Vous pouvez générer des phrases comme :

• La souris joue dans la cuisine
• Le chat et le chien nagent à minuit sous la table.

On souhaite que les phrases soient grammaticalement correctes : autrement dit, il faut conjuguer le verbe. Vous pouvez bien sûr augmenter la taille de votre liste de sujet en faisant varier la cardinalité (Le chat, des chats, un chat, trois chats). Il faut bien sur accorder le verbe en conséquence. En rajoutant des conjonctions de coordination (le fameux mais, ou, et, donc, or, ni, car) il est possible de complexifier les phrases assez simplement.

Vous disposez d'une liste de mots courants en Français ici et un rappel des règles de grammaire ici .

Pour la culture, c'est une approche qu'on va qualifier de système expert, car le système qu'on conçoit dispose d'une énorme connaissance lexicale, grammaticale et sémantique.

Génération avancée : prise en compte du sens et ontologie

Cependant, le soucis avec cette méthode, c'est qu'on peut facilement générer des phrases qui n'ont pas de sens. Par exemple : La souris mange le chat.

Pour pallier à ceci, vous pouvez mettre en place système ontologie. Par exemple, on peut définir une relation $<$ pour manger et dire que pour manger : $souris<chat$ , $viande<chien$ , $croquette<chat$ afin de signifier que le chat mange la souris, le chien mange de la viande… Grâce à ce système, il est possible de définir des contraintes sur les éléments tirés au sort et ainsi de donner du sens aux phrases.

L'ontologie peut être décrite avec des langages comme le Web Ontology Language. Protégé est un logiciel Open source d'édition d'ontologie. Afin de ne pas décrire tout ce qui est possible et imaginable, il est possible de générer de l'information et des faits avec ce qu'on appelle des moteurs d'inférence

Génération de phrases par chaîne de Markov

Thématique abordée : chaînes de Markov

Les chaînes de Markov sont un outil mathématique assez avancé, je ne ferai qu'une description superficielle de ces dernières.

L'idée principale derrière est de générer aléatoirement quelque chose de sorte que la probabilité de génération d'un élément ne dépende que du dernier élément généré. Par exemple, avec la chaîne de Markov suivante,

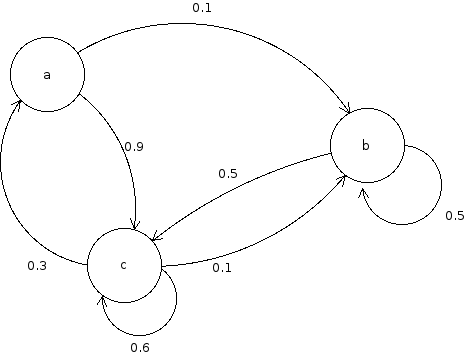
Si la lettre courante est 'a', la prochaine lettre peut être 'b' avec une probabilité de 0.1 (ce qu'on note $P(b|a)=0.1$, on parle de probabiliaaté conditionnelle) ou 'c' avec une probabilité de 0.9 ($P(c|a)=0.9$). Du point de vu mathématique, il est important que la somme des probabilités sortant d'un état (ici une lettre), soit égale à 1.

Pour appliquer ce concept à la génération de texte, on va remplacer nos simples lettres par des mots entiers.

le système doit d'abord passer par une phase d’apprentissage où on lui fournit des textes existants. De ces textes, le système va générer les chaînes de Markov correspondantes en reliant un mot au mot qui le suit. Par exemple si on lui donne les phrases

• Le chat mange la souris
• La souris mange le fromage

On va avoir :

De là, en se donnant juste un premier mot, il est possible de générer une phrase de façon aléatoire. Ce générateur n'a aucune connaissance de grammaire ni de syntaxe, dès lors la qualité de génération sera grandement influencée par la quantité et la diversité des textes que le système aura eu en phase d'apprentissage. Si vous intégrez la ponctuation comme élément de base dans les chaînes, il est possible de générer des textes entiers.

Conclusion

Voilà c'est à vous pour ce défi, on vous attends nombreux. Si vous des questions ou besoin d'aide, n'hésitez pas à demander !

Excellent, juste à la lecture du sujet, ça a l'air très évolutif ! Je sais que je dis ça tous les mois, mais je vais vraiment essayer de trouver le temps de le faire.

C'est plus 3 défis dans une thématique commune qu'un seul défi avec 3 étapes. J'ai fait ça pour brosser large et que pour chaque personne puisse faire quelque chose.

D'ailleurs, il n'y a pas spécialement de progression logique en terme de difficulté vu que la partie qui demande sûrement le moins de code est celle des chaînes de Markov. La génération de charabia n'est pas compliquée dans ses idées sous jacentes mais la gestion de l'unicode peut par contre un peu lourde en fonction du langage/framework utilisé (mais c'est aussi pour cela que je l'ai fait ^^). Enfin, la génération par dictionnaire est sûrement la partie la plus difficile car c'est la plus ouverte, surtout si on y rajoute les ontologies.

Très intéressant comme sujet . Il y a un subreddit assez marrant qui n'est peuplé que de bots générant des posts à partir de chaines de Markov : r/subredditsimulator. Il y a parfois quelques perles. Les différents bots utilisent différents subreddits pour la phase d'apprentissage.

Un truc connexe et assez marrant : le pipotron.

Et un (bon) cran au dessus, le générateur de papiers scientifiques. Pour ceux qui ne connaissent pas, ça vaut le détour !

Pour les chaines de Markov, une idée de où on peut trouver un corpus d'entrainement ? Et je suppose qu'il doit y avoir moyen de faire des chaines de Markov qui prennent en compte les $k$ derniers états ?

@Luthaf : https://www.gutenberg.org/

Et pour la 2e question, on peut très bien, mais ce n'est plus une chaine de Markov (par définition). Et attention, plus $k$ est grand, plus ton corpus d'entrainement devra être important pour donner quelque chose de valable.

Par extension, on lit souvent « chaîne/modèle de Markov d'ordre N ».

Sinon, ce défi est l'occasion de ressortir un générateur écrit il y a quelques mois qui se compose de plusieurs chaînes de Markov d'ordres différents (1 à N) et pondérées de façon à privilégier les chaînes d'ordre supérieur.

https://github.com/entwanne/sentences_generator/blob/master/generator.py

C'était à la base dans le but de faire un bot IRC qui analyserait les messages des gens pour ensuite prendre part aux discussions.

Il y a aussi le générateur de paroles de chansons de Patrick Sébastien (Bon ça vaut ce que ça vaut hein)

Sinon j'aime bien le sujet, je vais essayer de faire quelque chose si j'ai le temps.

j'vais faire mon relou de grammar nazi (étonnant que personne ne l'ait encore fait d'ailleurs ), mais j'ai trouvé un soucis de texte, dans la ligne juste après le titre "Génération avancée : prise en compte du sens et ontologie" : "c'est qu'on facilement avoir facilement générer" -> "c'est qu'on peut facilement générer", ou "c'est qu'on peut facilement avoir généré"?

sinon sujet pour le moins intéressant, mais j'ai encore le Javaquarium et le Sudoku à finir

Les chaînes de Markov ont ceci de sympa qu'elles ont tendance à reproduire le style de leur corpus d'apprentissage (comme générer des phrases "à la Victor Hugo" après avoir englouti l'intégrale des Misérables).

Je m'étais marré il y a quelques années à entraîner une chaîne d'ordre 2 en mélangeant à chaque fois deux œuvres complètement différentes l'une de l'autre du domaine public (p.ex. Le Rouge et le Noir de Stendhal avec La Divine Comédie de Dante Alighieri), et à mettre au défi les gens de retrouver les œuvres à partir d'une phrase relativement longue générée au moyen de cette chaîne, ça marchait drôlement bien.

Haha le sujet est cool. Il me rappelle beaucoup l'épreuve de programmation du Zérothon 2006 (que, pour la postérité, l'équipe Scatobeerz (may the Flocon Fraicheur be with you) avait remporté by a landslide et notamment grace à un gâteau au yaourt).

Salut, pour en aider certain, y'a cette vidéo pour les chaînes de Markov et la génération de mot.

C'est bien expliqué : https://www.youtube.com/watch?v=YsR7r2378j0

Bonsoir !

Ce sujet m'a l'air intéressant et c'est parfaitement l'occasion pour moi de m'entraîner au Python (je m'y suis mis il y a quelques jours) et aussi de reprendre un peu l'habitude de traîner et participer sur des forums (le site du zéro ça date :p).

Donc voici ma contribution pour la génération de charabia (j'essaierai de faire les autres sujets proposés aussi) :

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107

from sys import argv
import operator
import random
import numpy as np
import matplotlib.pyplot as plt

lang_dict = {}
lang_str = ["fr", "de", "es", "pt", "eo", "it", "tr", "sv", "pl", "da", "is",
            "fi", "cs"]
nb_lang = len(lang_str)

def generate_char():
    letter = random.uniform(0.0, 100.0)

    for inter in range(0, nb_poss):
        if inter == 0 and prob[letters[inter]] >= letter:
            return letters[inter]
        if inter == nb_poss - 1:
            return letters[inter]
        elif (  letter >= prob[letters[inter]] and
                letter <= prob[letters[inter + 1]]):
            return letters[inter + 1]

def draw_chart(str):
    occurrence = {}

    # Count occurrences in the output text
    for letter in str:
        occurrence[letter] = occurrence.get(letter, 0) + 1

    # Calculate frequencies
    for letter in letters:
        if letter in occurrence:
            occurrence[letter] = occurrence[letter] / length * 100

    occur_list = sorted(occurrence.items(), key=operator.itemgetter(0))

    x_legend = sorted(occurrence.keys())
    x_length = len(x_legend)
    x_value = [occurrence[x_legend[i]] for i in range(0, x_length)]
    x2_value = [prob_original[x_legend[i]] for i in range(0, x_length)]

    y_legend = np.arange(x_length)

    bar_width = 0.35
    opacity = 0.4
    error_config = {'ecolor': '0.3'}

    fig, ax = plt.subplots()

    rects1 = plt.bar(y_legend, x_value, bar_width,
                    alpha=opacity,
                    color='b',
                    error_kw=error_config,
                    label="Generated Text")

    rects2 = plt.bar(y_legend + bar_width, x2_value, bar_width,
                    alpha=opacity,
                    color='r',
                    error_kw=error_config,
                    label="Original language")

    plt.title("Fréquence d'apparition des lettres")
    plt.xticks(y_legend + bar_width, x_legend)
    plt.legend()

    plt.show()

# Init language param
lang = argv[1]
if lang not in lang_str:
    raise LangError("Please specify a valid language")
for iLang in range(0, nb_lang):
    lang_dict[lang_str[iLang]] = iLang

# Get the probabilites from the .csv file and sort them by value
with open("freqLetters.csv") as f:
    # We don't need the first line
    first = f.readline()
    lines = f.readlines()
prob = {}
for line in lines:
    number = line.strip("\n").split(',')
    result = float(number[lang_dict[lang] + 1])
    # Only need letters in the language alphabet
    if result != 0:
        prob[number[0]] = result
prob_list = sorted(prob.items(), key=operator.itemgetter(1)) 

# Extract only letters from the sorted list
letters = [item[0] for item in prob_list]
nb_poss = len(letters)

# Cumulate values in dict (but conserve original probabilities)
prob_original = prob.copy()
for letter in range(1, nb_poss):
    prob[letters[letter]] += prob[letters[letter - 1]]

# Generate the output string
length = int(argv[2])
output = ""
for iChar in range(0, length):
    output += generate_char()

print(output)

draw_chart(output)

Comme je l'ai dit, je viens de me mettre au Python et je suis sûr qu'il y a énormément de remarques à faire sur ce code (réalisé un peu rapidement je l'avoue), donc n'hésitez pas à me dire tout ce qui ne va pas. Pour ce qui est de la génération des nombres, j'ai fait assez simple mais en faisant mes recherches je suis tombé sur un article vraiment intéressant pour les curieux : Darts, Dice, and Coins: Sampling from a Discrete Distribution. Au passage, j'ai remarqué qu'il y avait deux fois la colonne "Allemand" dans le fichier .csv, je me suis permis pendant les tests d'enlever la deuxième apparition. Sinon, j'ai voulu découvrir matplot un peu donc j'ai fait en sorte que le programme affiche un graphique montrant la fréquence d'apparition des lettres dans le texte généré par rapport aux infos du fichier .csv.

Voilà, j'attends vos retours !

Merci pour l'article, c'est très intéressant. Dans la doc python, il y a deux recipes classiques à ce sujet (ceux que l'auteur intitule "Loaded Die from Fair Die" et "Roulette Wheel Selection") : https://docs.python.org/3.5/library/random.html?highlight=random#examples-and-recipes .

La thématique et le sujet 2 en sont directement inspirés (vu que j'avais participé à l'époque). Mais pas moyen de retrouver le sujet avant ton lien =/

Voici ce que j'ai fait en Haskell pour les chaines de Markov (d'ordre k). Pour la génération de la matrice de transition, on pondère simplement par le nombre d'occurrences de la transition donnée. Il y a des symboles de début et de fin (pas de génération infinie mais on peut adapter). Les noms des objets sont mal choisis.

J'ai fait avec ça un générateur de texte qui n'est pas super intéressant, ainsi qu'un générateur de prénoms qui donne de meilleurs trucs. Ça met 16 secondes à analyser les Misérables pour l'ordre 2…

Voici le code. Si vous avez des commentaires (notamment concernant des manières plus abstraites de faire les choses, avec des constructions générales, tout ça), je suis preneur.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131

module Markov where

import Control.Arrow hiding (loop)
import qualified Control.Category as C
import Control.Monad.State
import Control.Monad.Writer hiding (Endo)
import Control.Monad.Random hiding (split)
import Control.Monad.Identity
import Control.Monad.Trans.Maybe

import Data.Foldable
import qualified Data.Map as M
import Data.List.Split (split, keepDelimsR, oneOf)
import Data.Tuple (swap)
import Data.List (tails)

----------

x $> f = f x

(!) :: (Ord a) => M.Map a b -> a -> b
(!) = (M.!)

free_mon x = [x]

transpose :: [[a]] -> [[a]]
transpose []       = []
transpose (xs:xss) = xss
                  $> reverse
                  $> foldr (zipWith (:)) (map (\x -> [x]) xs)
                  $> map reverse

wrap_randt :: (RandomGen g, Monad m, Monad n) =>
              (m (a,g) -> n (b,g)) -> (RandT g m a -> RandT g n b)
wrap_randt f = runRandT >>> fmap f >>> liftRandT
-- pas super, on doit pouvoir mieux faire que ça

newtype Endo cat a = Endo {runEndo :: cat a a}

instance (C.Category cat) => Monoid (Endo cat a) where
  mempty = Endo C.id
  mappend f g = Endo $ (runEndo f) C.>>> (runEndo g)

loopM :: (Monad m) => (s -> m s) -> (s -> m s)
loopM = Kleisli >>> Endo >>> repeat >>> fold >>> runEndo >>> runKleisli

ensures :: (MonadPlus m) => (a -> Bool) -> (a -> m a)
ensures p = runKleisli $ (Kleisli (guard . p) &&& C.id) >>^ snd

liftK :: (MonadTrans t, Monad m) => Kleisli m a b -> Kleisli (t m) a b
liftK = runKleisli >>> liftK_ >>> Kleisli
liftK_ :: (MonadTrans t, Monad m) => (a -> m b) -> (a -> t m b)
liftK_ = fmap lift

----------

walk_until :: (Monad m) => (s -> Bool) -> (s -> m s) -> (s -> m ())
walk_until stop step = loopM (ensures (not . stop) >=> liftK_ step)
  >>> runMaybeT >>> fmap (const ())

type Markov_table st m =  M.Map st (M.Map (st,m) Integer)

next_symb :: (RandomGen g, Ord st, Monoid m) =>
             Markov_table st m -> (st -> RandT g (Writer m) st)
next_symb mt = let
    table_rand = fmap weighted_to_randwriter mt
    weighted_to_randwriter :: (RandomGen g, Ord st, Monoid m) =>
                              M.Map (st,m) Integer -> RandT g (Writer m) st
    weighted_to_randwriter = M.toList
                         >>> fmap (writer *** fromInteger)
                         >>> fromList
                         >>> fmap lift >>> join
  in (table_rand !)

list_to_markov_table :: (Ord st, Ord m) => [(st,(st,m))] -> Markov_table st m
list_to_markov_table = fmap (id *** (`M.singleton` 1))
                   >>> M.fromListWith (M.unionWith (+))

class Markov_atom a where
  start :: a
  is_end :: a -> Bool

data Markov_list s = ML [s] | ML_end | ML_start
  deriving (Eq, Ord, Show)

instance (Eq s) => Markov_atom (Markov_list s) where
  start = ML_start
  is_end = (== ML_end)

build_mt :: (Ord a, Monoid a) =>
            Integer -> [[a]] -> Markov_table (Markov_list a) a
build_mt k = map list_to_markov_lists
         >>> concat
         >>> list_to_markov_table
  where
  list_to_markov_lists :: (Ord a, Monoid a) =>
                          [a] -> [(Markov_list a, (Markov_list a, a))]
  list_to_markov_lists = tails
                    >>> take (fromInteger k)
                    >>> transpose
                    >>>  map ML         &&&  map ML       &&&  build_messages
                    >>> ([ML_start] ++) *** (++ [ML_end]) *** (++ [mempty])
                    >>> id *** (uncurry zip) >>> uncurry zip
    where
    build_messages [] = []
    build_messages (x:xs) = [foldr (<>) mempty x] ++ (map last xs)

random_walk :: (Ord a, Monoid m, RandomGen g, Markov_atom a) =>
               Markov_table a m -> Rand g m
random_walk = next_symb
          >>> walk_until is_end
          >>> ($ start)
          >>> wrap_randt (fmap snd >>> runWriter >>> swap >>> Identity)
          --- moche

text_to_mt :: Integer -> String -> Markov_table (Markov_list String) String
text_to_mt k = split (oneOf "\n")
           >>> filter (/= "\n")
           >>> map (split (keepDelimsR $ oneOf " "))
           >>> filter ((/= "") . concat)
           >>> build_mt k

imitate_speechs :: (RandomGen g) => Integer -> String -> Rand g String
imitate_speechs = curry $ (uncurry text_to_mt) >>> random_walk

words_to_mt :: (Ord a) =>
               Integer -> [[a]] -> Markov_table (Markov_list [a]) [a]
words_to_mt k = map (map free_mon) >>> build_mt k

imitate_words :: (RandomGen g, Ord a) => Integer -> [[a]] -> Rand g [a]
imitate_words = curry $ (uncurry words_to_mt) >>> random_walk

Et voici pour générer des prénoms aléatoires (pour du texte, enlever le lines et remplacer words par speechs). Arguments en ligne de commande : fichier d'exemple, puis ordre de la chaine, puis nombre de trucs générés (séparés par des retours à la ligne).

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

import Markov

import System.Environment (getArgs)
import System.IO
import Control.Monad
import Control.Arrow
import Control.Monad.Random

main :: IO ()
main = do
  args <- getArgs
  let [a, b, c] = args
      path_sample = a
      k = (read :: String -> Integer) b
      nb_imitations = (read :: String -> Integer) c
  withFile path_sample ReadMode (hGetContents >=> \sample -> do
    let k_imitations = lines sample
                    $> imitate_words k
                    $> replicateM (fromInteger nb_imitations)
    newStdGen >>= (evalRand k_imitations >>> unlines >>> return) >>= putStr)

J'aime bien l'idée de générateur de prénoms aléatoires.

Je ne sais pas exactement comment tu t'y es pris, mais j'ai fait de mon coté un petit script en python basé sur un corpus de prénoms existants pour voir ce que ça donne. Comme on pouvait s'y attendre le choix de N influence beaucoup les résultats, et dès N=3 les prénoms générés ne sont plus très originaux, une bonne part d'entre eux provenant directement du corpus.

Le code :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

from collections import Counter, defaultdict
from itertools import accumulate
from random import random, choice
from bisect import bisect

##  récupère une liste de prénoms francophones sur Wikipédia
import requests
import lxml.html

url = 'https://fr.wikipedia.org/wiki/Liste_de_pr%C3%A9noms_fran%C3%A7ais_et_de_la_francophonie'
gpath = '//*[@id="mw-content-text"]/dl[*]/dd[*]/b/span/a/text()'
r = requests.get(url)
doc = lxml.html.document_fromstring(r.text)
lst = doc.xpath(gpath)

## ordre de la chaîne de Markov
N = 2

def ngrams(s, n):
    "renvoie les n-grammes d'un mot (générateur)"
    return (s[i:i+n] for i in range(len(s)-n+1))

def weighted_choice(choices, cumdist):
    "choix aléatoire pondéré"
    return choices[bisect(cumdist, random() * cumdist[-1])]

# compte les occurences des n-grammes
counter = Counter()
for first_name in lst:
    counter.update(ngrams('^'+first_name+'$', N+1))

# prépare une table de probabilité conditionnelle
M = defaultdict(dict)
for k, v in counter.items():
    M[k[:-1]][k[-1]] = v

P = {}
for prefix, dct in M.items():
    choices, weights = zip(*dct.items())
    cumdist = list(accumulate(weights))
    P[prefix] = choices, cumdist

# générarion des prénoms
for _ in range(50):
    # choisit un début existant
    s = suffix = choice([k for k in P.keys() if k.startswith('^')])
    while suffix in P:
        s += weighted_choice(*P[suffix])
        suffix = s[-N:]
    print(s[1:-1])

Oui, en effet, je prenais k=2 pour générer les prénoms. Moi j'ai pris une liste de "prénoms anciens" trouvée sur un forum. Je procède de la même manière que dans ton code.

Je viens de modifier un peu mon code pour la gestion de walk_until (c'est devenu plus long avec les définitions auxiliaires mais je préfère ainsi).

Tiens, ça pourrait être rigolo de trouver une liste ordonnée des prénoms les plus donnés l'année passée et de se servir du classement pour pondérer les transitions entre digrammes…