Choix de chemin sous condition

a marqué ce sujet comme résolu.

Hey,

Puisse qu'il y a l'air d'y avoir une communauté mathématiques de qualité ici je m'adresse à vous.

Je me renseigne sur les graphes et l'optimisation (certains auront remarqué le thème des TIPE 2017).

Mon but est ici d'obtenir un chemin optimisé d'une source à une arrivée avec des contraintes sur les arrêtes que je définie pour l'instant de deux manieres : débit et prix d'ouverture

Je me suis déja pas mal renseigné sur le sujet et les problèmes parallèles comme le probleme de flot maximal (et toutes les versions classiques en découlantes comme les contraintes de prix par unité lineaire (au passage, avec une fonction concave vous pensez que c'est facilement faisable ? pur curiosité)).

Le problème c'est que je n'ai pas reussi à trouver de document traitant de mon probleme :

une source A doit produire un certain débit (disons 5ua) pour les acheminer vers un point B, en passant par des routes dont la construction est payante, il faut alors determiner la solution optimum :

graphe 1

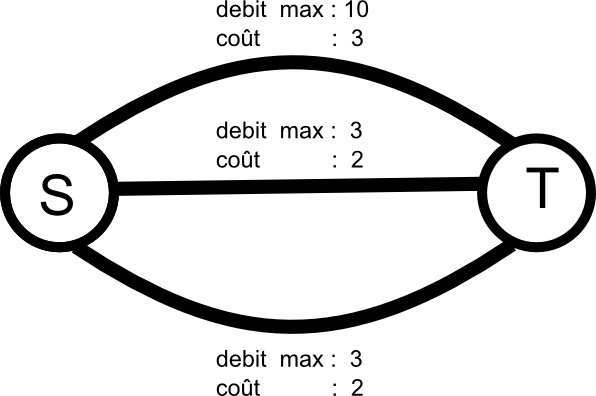
ici pour un debit de 5, ouvrir toutes les voies (prix 7), la voie du haut + une autre (prix 5), les deux voies du bas (4) ou juste la voie du haut (3) sont solutions mais seule la derniere est optimale

  • Pensez vous que l'on puisse retomber sur un probleme de flot maximum/ coupe-minimum ?
  • Dans le cas de graphes à deux sommets, pensez vous que revisiter les problemes à base du probleme du sac à dos puisse etre utile voir extensible à des graphes à plusieurs sommets ?
+0 -0

Salut,

Ton problème ressemble plus à de l'optimisation linéaire en nombres entiers. En gros, tu aurais des variables de décisons (valant 0 ou 1) et qui correspondraient à l'ouverture ou non des routes. Avec ça tu peux calculer le coût total (que tu souhaites minimiser) et tu es contraint par le flot maximal des routes ouvertes qui doit être supérieur ou égal à celui à transférer.

Le flot max/coupe min peut indiquer si le problème est faisable ou non.

+1 -0

Pour l'optimisation convexe, incluant un peu d'optimisation en nombre entiers, on pourra conseiller l'excellent cours de Gaubert, en particulier page 30 pour l'intégrité des points extrêmes (qui sont solutions en cas linéaire), chapitre 6 pour l'algorithme classique du Simplexe, et surtout chapitre 7 sur les coupes d'intégrités.

Rien ne t'empêche de jeter un coup d'oeil au reste évidemment. :)

Par ailleurs, ton problème est très mal posé. Tu ne donnes pas ce que tu veux optimiser clairement. Est-ce maximiser le débit pour un coût donné ou minimiser le coût pour un débit donné, ou optimiser les deux à la fois auquel cas la nature du problème et la résolution change complètement puisqu'il s'agit d'un problème multiobjectif où il existe un ensemble de compromis et pas une solution unique.

Je me doute qu'on est dans la minimisation du coût avec un débit donné, mais tu devrais vraiment clarifier ton énoncé.

+0 -0

En effet, j'ai posé le problème de manière assez imprécise avec l'idée d'une minimisation du coup pour un débit minimum mais là n'est pas tellement la question puisse que mon étude se base plutôt sur la modélisation et la résolution de tels systèmes. Disons que je verrai ce que j’étudierai en fonction des possibilités, cette idée de compromis est cela dit assez intéressante.

En tout cas merci pour les références ;)

+0 -0

J'aurais tendance à penser que le problème peut s'aborder avec de la programmation dynamique. Avec un graphe à deux sommets (comme sur ton schéma), c'est assez évidant. À partir de là, la généralisation à d'autres types de graphes me semble tout à fait possible.

En parcourant les arrêtes du graphe avec un parcours en largeur, on a le choix d'activer ou non une arrête. Pour chaque état, on peut calculer le débit maximum que va obtenir chaque nœud dans le graphe actuel. Le premier calcul permet de comparer les solutions et d'éliminer les solutions moins intéressantes que d'autres solutions (quand tous les nœuds ont un moins bon débit pour un coût total supérieur). Ça donne une solution de programmation dynamique1 probablement pas trop mauvaise qui te permettra d'obtenir tous les optimums de Pareto (donc pour le problème multiobjectif).

Ce qu'il y a de bien avec cette méthode, c'est que tu peux l'optimiser si tu ne cherche uniquement le prix optimal pour un débit minimum donné. Dans ce cas, tu peux aller plus loin dans l'élimination des états en calculant le débit maximum que peut obtenir le nœud final si on ajoute toutes les arrêtes non décidés. Ce deuxième calcul permet d'éliminer les états qui amènent à une solution non valide (le débit minimum n'est pas respecté). De même, tu peux calculer le prix minimum à payer pour atteindre la cible (sans prendre en compte le débit) que tu pourra comparer à des solutions possibles et ainsi éliminer à l'avance certains états que le prix minimum est plus grand que celui d'une solution. Dans les deux cas, le principe est de faire une prévision optimiste (peu coûteuse) et d'éliminer une branche complète à l'avance si celle-ci s'avère peu intéressante.

À noter que les solutions que j'ai proposé donnent les solutions optimales et pas juste de bonnes solutions.

  1. En fait, la programmation dynamique est assez similaire à l'exploration de l'arbre complet de décision. La grosse différence c'est que la programmation dynamique se fait de tel manière que l'on "élimine" certaines branches (la plupart du temps, on se contente de les fusionner) sans les explorer entièrement. ↩

+0 -0
Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte