Ça fait beaucoup de questions, je vais voir ce que je peux faire 
Je vais commencer par une petite auto-citation:
De manière générale, pour un opérateur $\hat{\mu}$ décrivant une transition entre deux fonctions d’ondes ($\Psi$) de l’état initial ($\Psi_i$) au final ($\Psi_f$), une transition est permise si:
$$\Gamma^{\Psi_f} \otimes \Gamma^{\hat{\mu}} \otimes \Gamma^{\Psi_i} \in \Gamma^{RTS}, \text{ alors } \int \Psi_i^\star\,\hat{\mu}\,\Psi_f d\tau\neq 0$$
où $\otimes$ représente le produit direct et $\Gamma^{RTS}$ est la représentation totalement symétrique. En effet, la transition n’est permise que si le produit $\Psi_i^\star\,\hat{\mu}\,\Psi_f$ ne donne pas une fonction qui soit impaire (puisque l’intégration sur tout l’espace d’une fonction impaire donne un résultat nul), et cette parité peut être déterminée en observant la parité des trois composants de celle-ci. On peut dès lors définir, pour chaque spectroscopie, une série de règles de sélection.
(…)
Une molécule possède $3N$ ($N$ étant le nombre d’atomes) degrés de liberté, dont 3 de rotation~(ou 2 si la molécule est linéaire) et 3 de translation, ce qui laisse $3N-6$ (ou $3N-5$) degrés de liberté de vibration. En spectroscopie vibrationnelle, une molécule est excitée de son niveau fondamental ($\Gamma^{\Psi_i} \in \Gamma^{RTS}$) à un état excité vibrationnel. Dès lors, la transition n’est possible à condition que $\Gamma^{\Psi_f}\otimes\Gamma^{\hat{\mu}} \in \Gamma^{RTS}$, c’est-à-dire que l’opérateur et l’état vibrationnel final appartiennent à la même représentation.
Par conséquent, un mode de vibration $a$, dont les coordonnées normales sont notées $Q_a$,
- Est actif en spectroscopie IR si $\partial \mu_i / \partial Q_a \neq 0$, autrement dit si le mode de vibration implique une modification du moment dipolaire. C’est le cas lorsque $Q_a$ appartient à la représentation irréductible d’une des composantes de translation ($i=x,y,z$) ;
- Est actif en spectroscopie Raman si $\partial \alpha_{ij} / \partial Q_a \neq 0$, autrement dit si le mode de vibration implique une modification de la polarisabilité. C’est le cas lorsque $Q_a$ appartient à la même représentation irréductible qu’une fonction quadratique ($ij =xx\,(x^2)$, $xy$, ....).
Donc en effet, il y a cette fameuse intégrale. En fait, impliquer la théorie des groupes là dedans reviens au final à avoir un peu de bon sens mathématique: par exemple, si $\Psi_i^\star\,\hat{\mu}\,\Psi_f$ est impaire, l’intégration sur tout l’espace donnera quelque chose de nul. Et ainsi de suite. La "représentation totalement symétrique" (R.T.S) est effectivement irréductible, mais aussi (et surtout) présente un caractère égal à un pour chacune des classes d’un groupe. La représentation R.T.S., c’est toujours la première ligne d’une table de caractère (donc la $A$, $A_1$, $A_g$ …). Et je rappelle qu’avoir un caractère égal à 1 signifie "invariant à cette transformation de symétrie", donc si par exemple le groupe contient une inversion, $\chi(i)=1$ signifie que ce qu’on considère est pair. Et ainsi de suite, d’où l’intérêt de la théorie des groupes dans ce genre de cas.
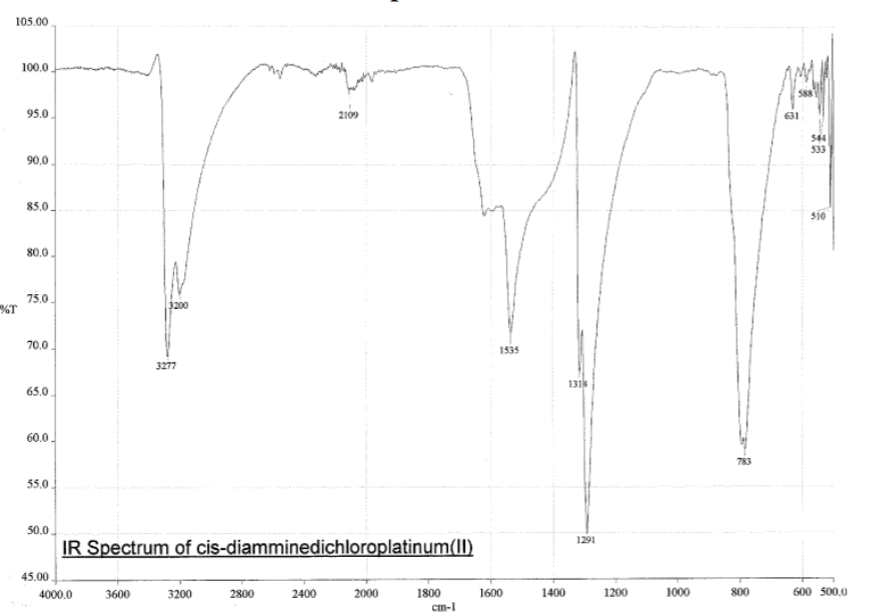
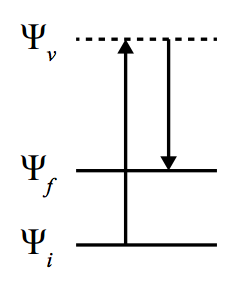
Cette règle vaut pour un grand nombre de spectroscopies, et ce traduit par ce que vous connaissez mieux sous le nom de "règles de sélections". C’est ces fameuses règles de sélections qui empêchent techniquement de voir certains pics dans les spectres UV des complexes (en pratique, on les vois, mais leur $\epsilon$ est beaucoup plus faible), c’est ces fameuses règles de sélections qui empêche d’observer certaines transition en UV et en Raman ("tout simplement" parce que le moment dipolaire se transforme comme la translation et que la polarisabilité se transforme comme les machins quadratiques), et ainsi de suite. L’histoire du niveau virtuel en Raman n’est pas spécialement importante ici, il s’agit juste d’une spectroscopie vibrationnelle complémentaire puisque les règles de sélections sont différentes, ce qui permet d’observer d’autres transitions qu’en IR. Les intensités sont pas pareilles non plus, c’est une spectroscopie ou, par exemple, y’a pas de grosse "patate" à 3400 cm⁻¹ à cause de l’eau si je dis pas de conneries.
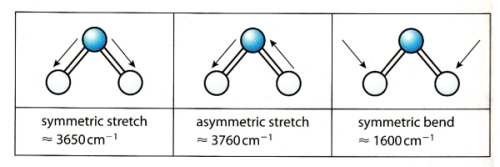
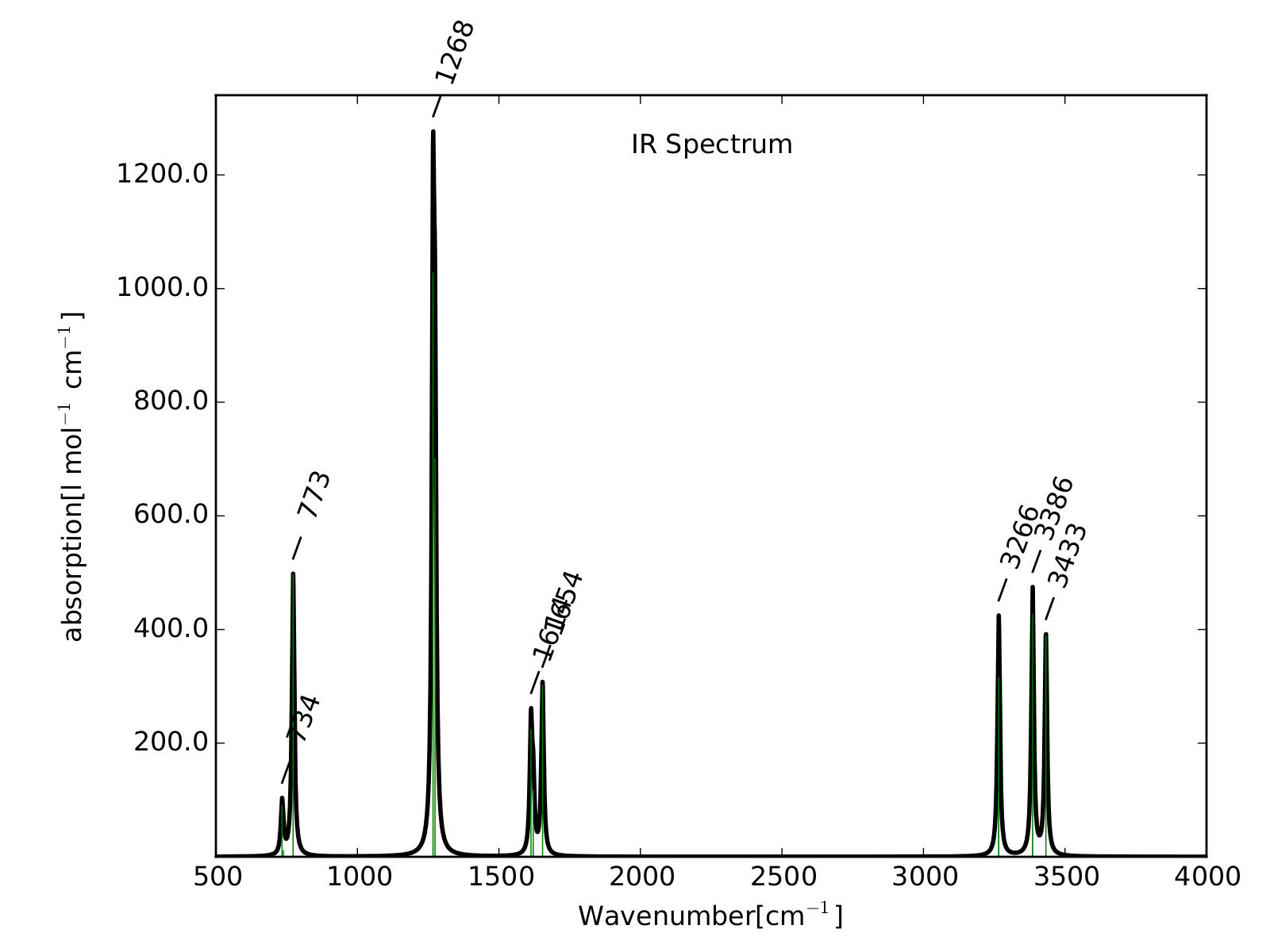
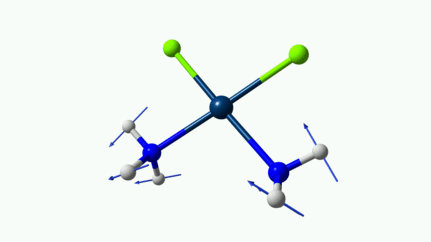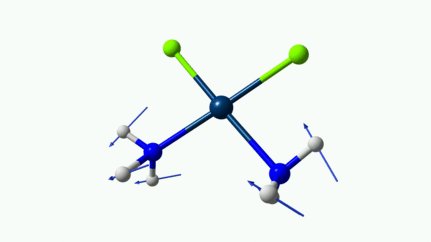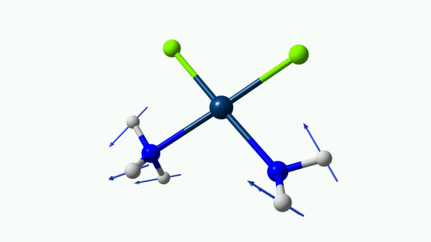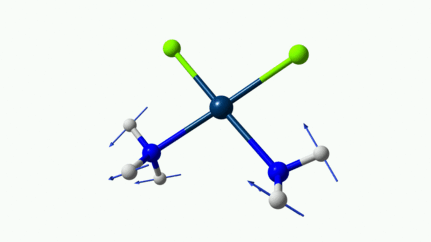
Juste pour être sûr, les 2 dernières animations (3511 et 3560 cm-1) représentent bel et bien un stretching aussi?
et
J’pense bien que les 3 dernières animations sont des stretching, mais je dirais ne pas savoir dire si c’est asymétrique ou symétrique.
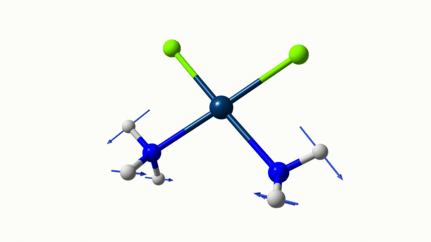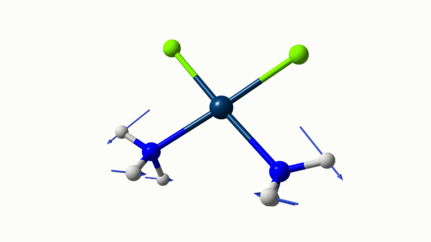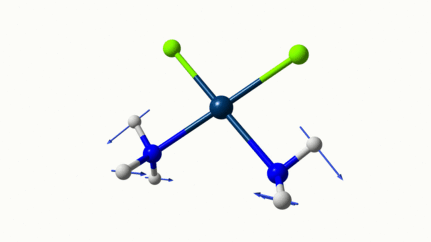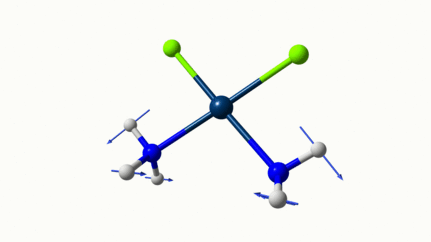
Me semble bien que c’est du stretching aussi. Après, ça me fait toujours un peu rigoler, parce que personne, sur 5 ans d’études, ne m’as jamais dit "un stretching, c’est ça". Donc je me dis que c’est un stretching, par analogie avec l’eau, parce qu’il semble impliquer des modifications de longueur de liaison, et je me dis que c’est asymétrique parce que ce qui se passe sur l’azote de gauche est à l’inverse de ce qui se passe sur l’azote de droite, mais je vous avoue que c’est plus du bon sens qu’une vérité pure. Me croyez pas sur parole sur celle là.
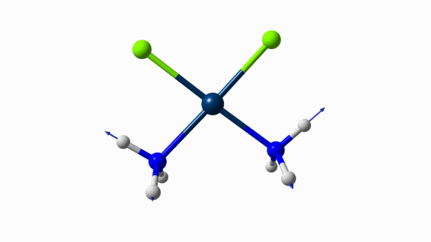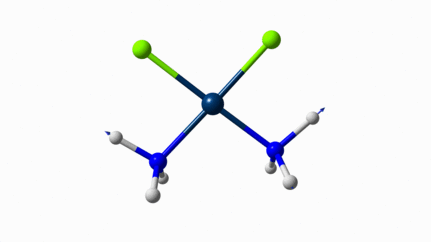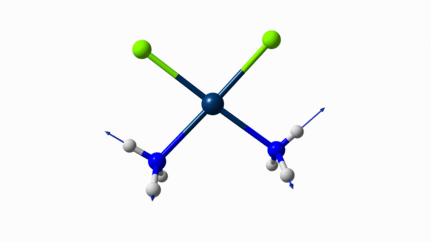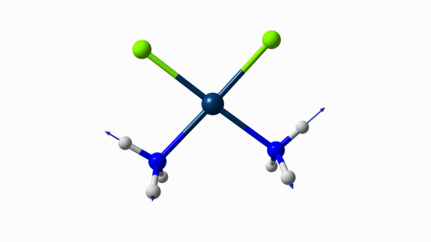
D’ailleurs à 1314 cm−1 est-ce que ce mouvement est lié à l’effet parapluie d’inversion des trialkyles amines prochirales ?
On dirait, hein ? 
Notez que sur celle là, je crois me souvenir que techniquement, c’est un effet "anharmonique", ce qui signifie que la simulation ne la place pas exactement à la bonne place. Mais peu importe ici.
Sinon,
(…) mais là ça me donne vachement envie ! La seule chose qui me dérange c’est "on multiplie par X pour mieux reproduire les données expérimentales", ça fait très "magie".
Ça fait pas que "magique", c’est "magique". Mon but n’est pas non plus de vous vendre la chimie quantique comme un truc parfait, parce que c’est évidement pas le cas en pratique. Hartree-Fock, la DFT ou d’autres sont des approximation de la réalité (puisque c’est un problème à $N$ corps et qu’on a pas de solution simple pour les problèmes à plus de 3 corps), et donc ce qu’on obtient sont des approximation de la réalité, entachées de différentes erreurs. Un des buts d’un cours de chimie quantique devrait justement être de pointer ces erreurs, et dès lors d’expliquer dans quel cadre on a le droit d’utiliser certaines méthodes.
Par exemple, si c’est la précision que je cherche, je suis à côté de la plaque. Et en même temps, j’ai pas non plus cherché à tenter de l’obtenir. J’ai dit que mon calcul avait duré 4 minutes, même sans vous expliquer ce qu’il y a derrière, je peux vous dire que c’est très peu. Il est évident que plus la méthode que j’utilise est complexe/complète, plus je m’attend à obtenir un résultat précis, mais plus ça va me prendre du temps à l’obtenir. J’aurais pu, par exemple, inclure l’effet du solvant, ce qui aurait probablement multiplié le temps du calcul par 3 ou 4, mais m’aurait probablement rapproché du spectre expérimental. Et ainsi de suite. Cependant, des générations de chimistes théoriciens on constatés que si on faisait une régression linéaire entre les longueurs d’onde expérimentales et calculées au niveau d’approximation que j’ai utilisé, ben le coefficient de régression linéaire de la droite était de 0.964. Il faut traduire ça par "ce qui manque dans la méthode peu être rajouté en multipliant par ce facteur". Il se trouve que c’est très courant en simulation de spectroscopie sous une forme ou une autre, et que je suis d’accord, c’est "magique".
Maintenant, il faut être pragmatique. Moi, j’ai clairement choisi la facilité, alors que j’aurais pu employer une méthode un peu plus complexe et mon calcul aurait duré quelques heures. Ça m’aurait pas coûté grand chose de plus, mais je voulais avoir le résultat rapidement, et mon but n’était absolument pas de donner un résultat parfait. Mais au delà de ça, il y a des gens qui se basent sur la chimie quantique pour guider des processus ou des synthèses (bon, c’est rare, mais il y en a de plus en plus). Mettons que le calcul en question prennent plusieurs mois, ça fait plusieurs mois à attendre un résultat avant de continuer. Pas top ! Maintenant, si la même réponse peut être obtenue en quelques jours en multipliant le résultat par 0.964, ben … Le patron va y regarder à deux fois. Mais il ne faut pas sur-vendre le résultat non plus, ça reste une simulation, et y’a certains cas ou ça fonctionne très bien, d’autre ou ça ne fonctionne pas. En général, ce qu’on fait, c’est qu’on modélise un système de petite taille avec une méthode très complexe, puis qu’on compare avec les résultats de méthodes plus simple pour trouver celle qui donne un résultat "correct" en un temps acceptable. Puis on simule les gros systèmes avec cette méthode plus simple 
Donc voilà: la chimie quantique est un outil génial quand on sais l’utiliser, mais on doit bien être conscient de ces faiblesses et de ces limites … Comme toute technique 
C’était le paragraphe auto-conviction
Par contre, j’ai pas très bien compris comment tu lance ça. Tu modélise sur GAMESS/Gaussian 09 suivant ton choix et puis pourquoi tu passes sur Avogadro ? Je pensais que GAMESS pouvait te donner directement le "petit film" de ce que tu avais modélisé.
Alors, pas confondre. GAMESS et Gaussian sont des programmes de calculs. Autrement dit, eux, ce qu’ils font, c’est calculer la fonction d’onde (et l’énergie) et éventuellement l’utiliser pour calculer des propriétés additionnelles (moment dipolaire, RMN, IR, etc). Propriétés qu’ils crachent sous forme de texte, parce qu’ils ont été créé dans les années 80 et écrit en Fortran et que histoire de l’informatique toussa. Donc non, malheureusement, GAMESS (ou Gaussian) est pas foutu de sortir la moindre image. Par contre, si tu lui demande gentiment, il te sort les informations qui te permettent de la tracer (sous forme d’un tableau de chiffre).
C’est là qu’Avogadro (ou autres, mais celui là est gratuit et fait assez bien le job) qui n’est pas un programme de calcul, mais un programme de visualisation, entre en jeu. Lui, il lit les données et les interprète pour justement obtenir une jolie image, avec toutes les facilités de l’informatique moderne (GUI, boutons, souris, … Tout ces trucs qui existaient pas dans les années 80 quoi  ). Bref, c’est bien sympa pour donner du sens à toutes ces colonnes de chiffre.
). Bref, c’est bien sympa pour donner du sens à toutes ces colonnes de chiffre.
Vous me devez un café.






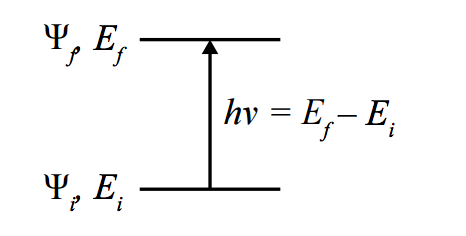
 Les petites animations envoient du lourd!
Pour la petite anecdote, l’année prochaine j’ai le choix d’un module de chimie computationelle (Monte Carlo, intro aux structures électroniques, …) et j’avoue que ça me tentais pas trop (depuis ma tentative de simulation de SN2..) mais là ça me donne vachement envie ! La seule chose qui me dérange c’est "on multiplie par X pour mieux reproduire les données expérimentales", ça fait très "magie".
Les petites animations envoient du lourd!
Pour la petite anecdote, l’année prochaine j’ai le choix d’un module de chimie computationelle (Monte Carlo, intro aux structures électroniques, …) et j’avoue que ça me tentais pas trop (depuis ma tentative de simulation de SN2..) mais là ça me donne vachement envie ! La seule chose qui me dérange c’est "on multiplie par X pour mieux reproduire les données expérimentales", ça fait très "magie".