Bonjour,
Je ne suis pas bon en math, fin… j’ai des bases mais concrètement je ne me considère pas comme bon.
Je suis en train de créer un petit programme, dans ce programme je voudrai afficher un résultat en fonction d’une donnée. Le problème c’est que je ne connais pas la fonction permettant d’arriver au résultat.
Par observation je connais toute un série de point de la courbe… mais me voilà bien incapable d’en extraire la fonction. Pouvez-vous m’aider ?
Voici le début de la série:
1 2 | X: 1, 2, 3, 4, 5, ..., 21, 22, 23, 24, ..., 37, 38, 39, ... Y: 0, 5, 11, 17, 23, ..., 120, 127, 134, 141, ..., 233, 241, 289, ... |
De ce que je vois, du rang 1 à 2 on fait +5, du rang 2 à 21 on fait +6 pour chaque valeur, du rang 21 au rang 37 on fait +7 pour chaque valeur de x et ainsi de suite.
Malheureusement à par constaté cela et remarque qu’avec le temps cela progresse de plus en plus vite… je suis bien incapable d’en retirer la formule.
Un graph illustrant la fonction:
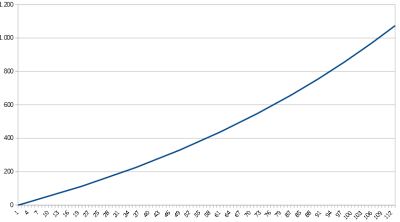
Pouvez-vous m’aider ?
Merci d’avance.
Cordialement, La source.







