Coucou les petits pépins physiciens,
Dans le cadre de la quantification de l’énergie via l’équation de Schrödinger suivante :
Je suis amené à étudier deux énergies potentielles aux formes différentes :
1. Saut de potentiel
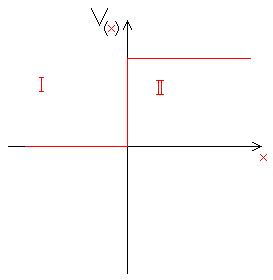
A ce moment je dois exprimer $\mathrm{ \psi_{(I)}}$ et $\mathrm{ \psi_{(II)}}$ en donction de $\mathrm{x}$ à l’aide de l’équation différentielle d’ordre 2 :
Avec pour $\mathrm{V_{(0)} = V_0}$ seule valeur de $\mathrm{V \neq 0}$.
Région (I)
J’écris le résultat sous forme de combinaison d’exponentielle :
Région (II)
J’écris le résultat sous forme de combinaison d’exponentielle :
Je ne saisis pas bien pourquoi dans ce résultat le $i$ disparaît par rapport à la première région. Je crois que c’est une histoire de dérivés ou de signe ?
Et là si je ne dis pas de bêtise le terme en $\mathrm{Cexp\left(\frac{\sqrt{2m(V_0-E)}x}{\hbar}\right)}$ possède une allure de courbe qui est non-bornée, car en $+ \infty $ la fonction continue à progresser (?) donc on doit le faire disparaître avec $\mathrm{C = 0}$ car physiquement $$\mathrm{\psi}$$ est une fonction bornée.
Conclusion
On obtient alors :
Par continuité en $\mathrm{x=0}$ on peut obtenir :
Les fonctions doivent être égales en ce point donc :
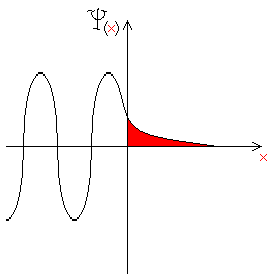
Et je ne sais pas comment on en arrive à tracer ce comportement qui ne suit pas la logique de la mécanique classique :
2. Barrière de potentiel
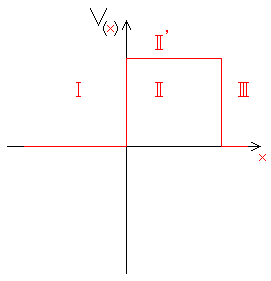
A ce moment je dois exprimer $\mathrm{ \psi_{(I)}}$, $\mathrm{ \psi_{(II)}}$ et $\mathrm{ \psi_{(III)}}$ en donction de $\mathrm{x}$ à l’aide de l’équation différentielle d’ordre 2 :
Mais je du mal à voir quel vont être les changements s’il y en a. Et comment comprendre la zone $\mathrm{(II')}$
Si vous aviez des éléments de réponses, ça m’aiderais beaucoup ! Merci pour le temps de lecture accordé.






 . C’est vraiment l’aspect math tout con que j’arrive pas à "lire" ou "comprendre". Les phénomènes en soit je les ais compris. C’est justement parce que c’est stylé comme comportement que j’aimerais réussir à comprendre les mathématiques derrière.
. C’est vraiment l’aspect math tout con que j’arrive pas à "lire" ou "comprendre". Les phénomènes en soit je les ais compris. C’est justement parce que c’est stylé comme comportement que j’aimerais réussir à comprendre les mathématiques derrière.
 ), tu as une équation de la forme
), tu as une équation de la forme  . Il ne me manque plus qu’à piger comment on trace la partie amortie (rouge) de
. Il ne me manque plus qu’à piger comment on trace la partie amortie (rouge) de 