Salut les agrumes,
Comme j’avais un peu prévenu les copains ici, je sors un sujet sur mon examen de mécanique quantique. Je vais retranscrire les questions de l’examen et chacune de mes réponses en balise secret. J’aurais donc besoin de votre discernement et de vos conseils/avis sur les réponses.
C’est un peu étrange pour un étudiant de revenir sur un de ces fails (en tout cas ça n’a jamais été mon genre), j’essaye justement par ce biais ne plus avoir aucun problème avec la mécanique quantique à l’avenir (  ).
).
A. Atome de Néon (Z = 10), équation de Scrödinger
Soit un atome de néon formé d’un noyau de masse $\mathrm{M}$ et de $\mathrm{Z}$ électrons de charge $\mathrm{-e}$ et de masse $\mathrm{m_e}$. Il s’agit de construire la fonction de Hamilton $\mathrm{H}$ de ce système, puis de trouver l’équation de Schrödinger correspondante.
1.Combien de termes d’énergie cinétique la fonction $\mathrm{H}$ contient-elle ?
Je pense à 2 termes distincts :
2.Combien de termes d’origine coulombienne la fonction $\mathrm{H}$ contient-elle ?
Je pense à 2 termes distincts :
3.Ecrire à présent $\mathrm{H}$ en fonction de $\mathrm{Z}$, $\mathrm{m_e}$, $\mathrm{M}$ des positions relatives des électrons et du noyau et de leurs impulsions :
J’imagine qu’ils veulent que l’ont sommes les termes pour créer $\mathrm{V_{(\vec{r})}}$ et ainsi avoir :
4.Construire l’équation de Schrödinger correspondante. On explicitera la démarche en détails.
5.Cette démarche dépend-elle du repère utilisé dans l’espace des configurations ?
Je ne sais pas du tout ce qu’est l’espace de configuration et je ne comprend pas à quelle point la dépendance radiale est générale. 
6.Proposer une méthode pour résoudre cette équation ?
Je pense à la séparation des variables du genre :
Ce qui permet d’obtenir 2 équation différentielle solvable, d’autant qu’ici on connait bien la forme de $\mathrm{V_{(\vec{r})}}$.
B. Etats stationnaires dans un puits de potentiel
On considère les états stationnaires d’une particule d’énergie totale positive dans une puits de potentiel infiniment profond (potentiel nul pour $\mathrm{0 < x < a}$ et infinie partout ailleurs).
a) Ecrire les expressions des fonctions d’onde dans les trois régions ($\mathrm{x<0}$, $\mathrm{0 < x < a}$, $\mathrm{a < x}$);
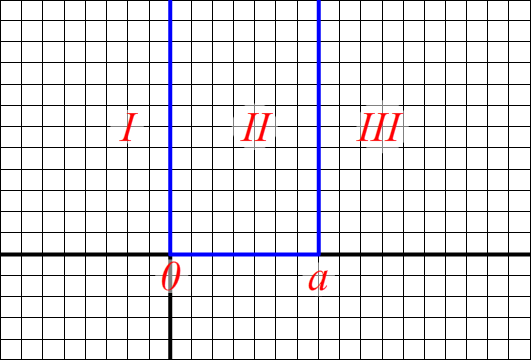
Je pars de l’équation de Schrödinger Stationnaire :
Je forme l’équation différentielle homogène :
Région $I$ :
Afficher/Masquer le contenu masqué$\mathrm{k^2 = \dfrac{2m}{\hbar^2} (V_{\infty} - E) }$
Polynôme caractéristique :
Afficher/Masquer le contenu masqué$A' = 0$ car la particule vient de la droite.
Région $II$ :
Afficher/Masquer le contenu masqué$\mathrm{\ell^2 = \dfrac{2mE}{\hbar^2} }$
Polynôme caractéristique :
Afficher/Masquer le contenu masquéRégion $III$ :
Afficher/Masquer le contenu masqué$\mathrm{k^2 = \dfrac{2m}{\hbar^2} (V_{\infty} - E) }$
Polynôme caractéristique :
Afficher/Masquer le contenu masqué$C = 0$ car la particule vient de la gauche.
b) En sachant que le potentiel est infini en dehors de l’intervalle $[0,a]$, par quoi peut-on approximer les fonctions d’onde dans les régions $I$ et $III$ ?
On peut approximer à $0$ les fonctions d’ondes stationnaires, car l’onde évanescente correspondante possède une faible portée, sachant que le potentiel ne redescend pas sous forme de barrière de potentiel plus loin, la particule n’a vraiment pas de probabilité d’exister dans ces zones.
C) Ecrire les conditions de continuité en $\mathrm{x=0}$ et $\mathrm{x=a}$.
Voici les égalité de raccordement :
$\mathrm{ \varphi_{I(0)} = \varphi_{II(0)}}$
$\mathrm{ A = B + B'}$
$\mathrm{ \dfrac{d\varphi_{I(0)}}{dx} = \dfrac{d\varphi_{II(0)}}{dx}}$
$\mathrm{ kA = i \ell B - i \ell B'}$
$\mathrm{ \varphi_{II(a)} = \varphi_{III(a)}}$
$\mathrm{ Be^{i \ell a} + B'e^{-i \ell a} = C'e^{-ka}}$$
$\mathrm{ \dfrac{d\varphi_{II(a)}}{dx} = \dfrac{d\varphi_{III(a)}}{dx} }$
$\mathrm{ i \ell Be^{i \ell a} - i \ell B'e^{-i \ell a} = -kC'e^{-ka}}$
d) Déduire la condition de quantification de l’énergie et la fonction d’onde à l’intérieur du puits ?
Euh là je sèche en fait, et c’est à partir de là que tout se cors à fond. 
e) En utilisant le fait que la fonction d’onde doit être normée, déduire la constante qui intervient dans l’expression de la fonction d’onde déduite au point d).
La seul fonction de normalisation que je connais c’est de déduire :
Mais vue que j’ai pas la solution de $d$ je ne sais pas vraiment où aller.
f) Donner les valeurs des énergies et des fonctions d’onde correspondant à $n=1,2,3$ où $n$ est le nombre quantique qui intervient dans la condition de quantification.
Bouarf, ça s’arrange pas. Je pense qu’il faut que je trouve $k_n = f(E_n)$.
g) Tracer les densités de probabilité de présence pour $n=1,2,3$.
…
J’espère que vous avez eu un peu de courage pour lire quelques unes de mes réponses/difficultés. Dîtes tout ce que vous pouvez/voulez en tout cas. J’suis à votre écoute pour mieux saisir les questions 


 )
)  )
)