Bonjour à tous,
Je révise pour un examen de spectroscopie et voici une question que je comprends pas (du moins, j’essaye de répondre - si quelqu’un sait me dire ce qui est juste / faux ça m’aiderait).
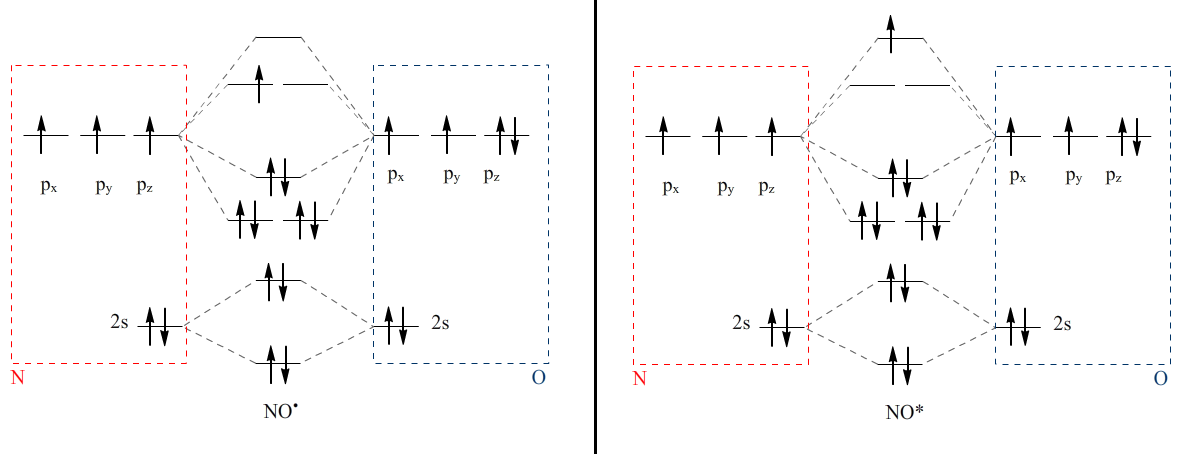
On me donne 2 configurations de NO: une à l’était fondamental et une excitée (1 électron promu au-dessus).
1. Prévoir la stabilité et la longueur de liaison relative
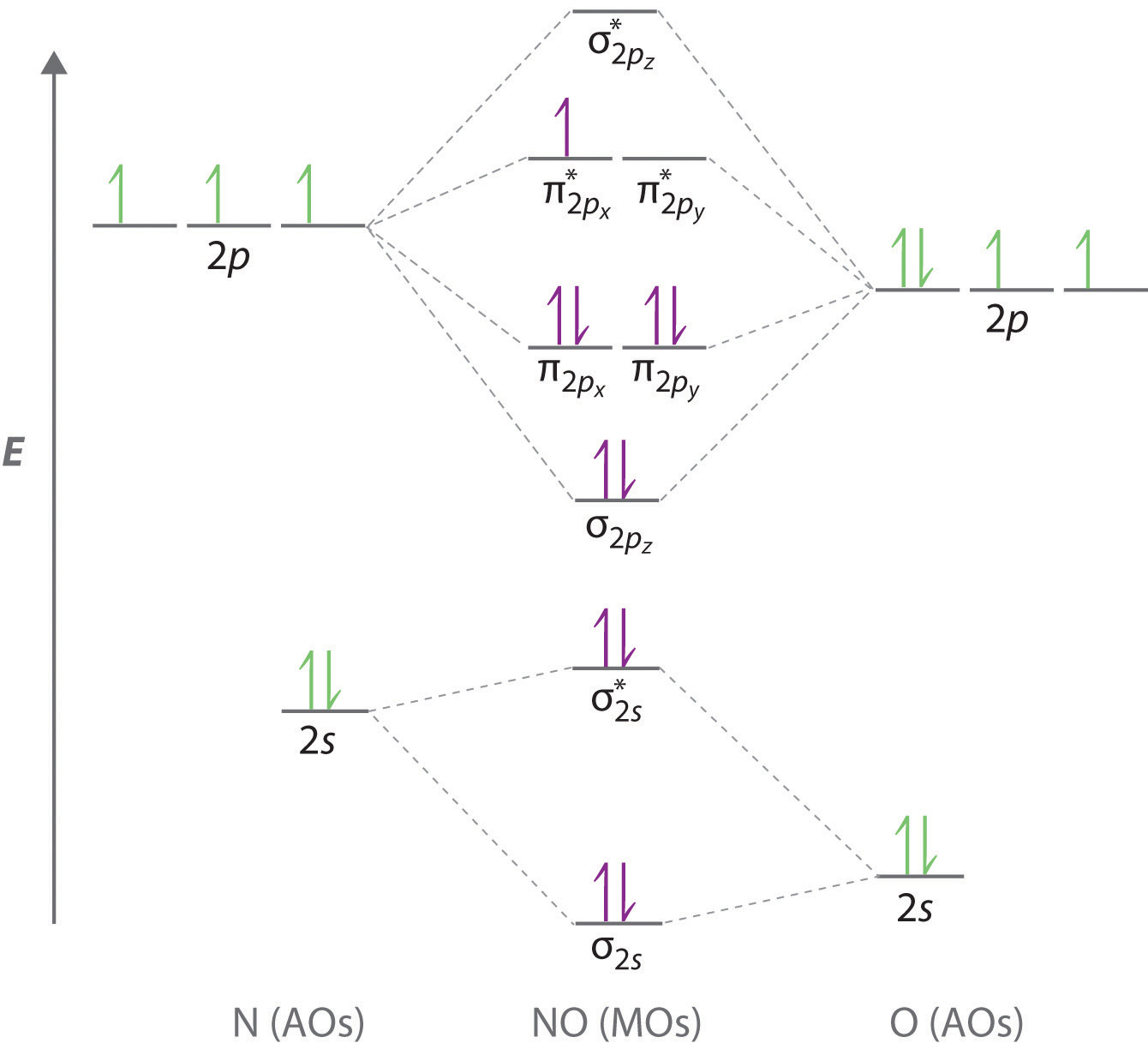
Je suppose qu’il faut calculer l’ordre de liaison. Je trouve 5/2 pour l’état fondemantal et 3/2 pour l’excité. L’état fondamental est donc plus stable. D’où cette formule vient-elle par contre et en quoi ça relie la stabilité?
Pour la longueur de liaison, elle change car elle est déterminée par le nombre d’électron liants (juste?). Les triples liaisons étant plus courtes que les simples, le ground state aura une longueur plus petite que l’état excité.
2. Dessiner les courbes de potentiel
Je suppose qu’il faut dessiner un potentiel de Morse (si on considère l’approximation du Rotateur Rigide). Sinon pour le potentiel réel je vois pas?

2. Dessiner le spectre d’excitation
Alors ici, je suis totalement perdu et je vois pas ce qu’il veut. On a vu en cours Franck-Cordon. Est-ce que ça peut avoir un lien?
Merci d’avance pour votre aide!