La cryptographie est un mot que vous connaissez sans doute. Je suis presque certain que vous avez fabriqué, dans votre enfance, quelques petits codes secrets. Des méthodes pour chiffrer des messages, il y en a des paquets, et je pars donc du principe que vous en connaissez (au moins, ayez lu ce tuto, ainsi que la suite). Tout ne sera pas abordé, mais cela vous permettra d’avoir un bon aperçu sur la chose avant de commencer.
La cryptologie est séparée en deux grandes parties : la cryptographie (comment faire des messages chiffrés), et la cryptanalyse (l’art de les casser). Ce tuto a pour but de vous présenter rapidement quelques outils de cryptanalyse sur des méthodes de codage d’antan. Mais il y a de quoi faire, ne vous inquiétez pas  . Sans plus de manières, c’est parti, on y va !
. Sans plus de manières, c’est parti, on y va !
- Le décalage et la recherche exhaustive
- La substitution et l'analyse de fréquences
- L'analyse de bigrammes
- Vigenere et l'indice de coïncidence
Le décalage et la recherche exhaustive
Commençons par le début du commencement : le chiffre de César, ou chiffrement par décalage. Pour rappel, cette méthode consiste à décaler les lettres d’un certain nombre de places dans l’alphabet.
Comment casser le code de César ? Si on connait le décalage, ça va : on fait le décalage dans l’autre sens. Mais comment faire si on ne l’a pas ?
Recherche exhaustive
Comme il y a 26 lettres dans l’alphabet, il n’y a que 26 décalages possibles (25 si on exclut le décalage de 0). On va donc faire une recherche exhaustive, c’est-à-dire que l’on teste toutes les possibilités ! Tôt ou tard on finira par tomber sur le bon résultat.
Exemple :
Texte chiffré : at rdst rthpg, r’thi uprxat p rphhtg
On teste alors les 26 décalages (on peut le faire à la main, mais on peut aussi le faire avec un petit programme).
Résultats :
- Decalage de 0 : at rdst rthpg, r’thi uprxat p rphhtg
- Decalage de 1 : bu setu suiqh, s’uij vqsybu q sqiiuh
- Decalage de 2 : cv tfuv tvjri, t’vjk wrtzcv r trjjvi
- Decalage de 3 : dw ugvw uwksj, u’wkl xsuadw s uskkwj
- Decalage de 4 : ex vhwx vxltk, v’xlm ytvbex t vtllxk
- Decalage de 5 : fy wixy wymul, w’ymn zuwcfy u wummyl
- Decalage de 6 : gz xjyz xznvm, x’zno avxdgz v xvnnzm
- Decalage de 7 : ha ykza yaown, y’aop bwyeha w ywooan
- Decalage de 8 : ib zlab zbpxo, z’bpq cxzfib x zxppbo
- Decalage de 9 : jc ambc acqyp, a’cqr dyagjc y ayqqcp
- Decalage de 10 : kd bncd bdrzq, b’drs ezbhkd z bzrrdq
- Decalage de 11 : le code cesar, c’est facile a casser
- Decalage de 12 : mf dpef dftbs, d’ftu gbdjmf b dbttfs
- Decalage de 13 : ng eqfg eguct, e’guv hcekng c ecuugt
- Decalage de 14 : oh frgh fhvdu, f’hvw idfloh d fdvvhu
- Decalage de 15 : pi gshi giwev, g’iwx jegmpi e gewwiv
- Decalage de 16 : qj htij hjxfw, h’jxy kfhnqj f hfxxjw
- Decalage de 17 : rk iujk ikygx, i’kyz lgiork g igyykx
- Decalage de 18 : sl jvkl jlzhy, j’lza mhjpsl h jhzzly
- Decalage de 19 : tm kwlm kmaiz, k’mab nikqtm i kiaamz
- Decalage de 20 : un lxmn lnbja, l’nbc ojlrun j ljbbna
- Decalage de 21 : vo myno mockb, m’ocd pkmsvo k mkccob
- Decalage de 22 : wp nzop npdlc, n’pde qlntwp l nlddpc
- Decalage de 23 : xq oapq oqemd, o’qef rmouxq m omeeqd
- Decalage de 24 : yr pbqr prfne, p’rfg snpvyr n pnffre
- Decalage de 25 : zs qcrs qsgof, q’sgh toqwzs o qoggsf
Le décalage de 11 à l’air plutôt suspect : le code cesar, c’est facile a casser.
Voilà, on a réussi à casser le code de César sans trop s’embêter ! Cette technique va fonctionner avec n’importe quel message, de n’importe quelle longueur, chiffré par décalage.
Autre technique : trouver une lettre
Si l’on a pas envie de tester les 25 possibilités, il est également possible de tenter de deviner le décalage. Par exemple, dans at rdst rthpg, r’thi uprxat p rphhtg, on voit que le t revient souvent. On peut donc se dire que le e du message initial a été chiffré en un t : ça semble pertinent. Cela nous donne un décalage de 15. Pour vérifier notre hypothèse, il suffit alors de tester en décalant tout de 15 lettres dans l’autre sens (décaler de -15 revient à faire +11 car $-15+26=11$) dans le texte chiffré. On retrouve alors bien le message escompté, et sans avoir tout calculé  .
.
On va maintenant passer à des méthodes un peu plus sophistiquées, parce que là, ce n’était pas sorcier  .
.
La substitution et l'analyse de fréquences
Après le chiffre de César, voyons la substitution monoalphabétique. Celle-ci consiste à utiliser une permutation où chaque lettre de l’alphabet sera remplacée par une autre lettre. Par exemple, tous les z du texte deviendront des e, et tous les s des t, etc.
Le code de César est donc une substitution particulière.
Les limites de la recherche exhaustive
On pourrait se dire que la recherche exhaustive devrait fonctionner, non ? En théorie, oui, mais en pratique, calculons un peu le nombre de substitutions possibles : le a peut devenir un a, un b, … ou un z. Ça fait $26$ possibilités. Le b peut devenir tout sauf la même chose que le a : $25$ possibilités et ainsi de suite jusqu’au z. Cela fait en tout $26*25*...*1 = 26!$ possibilités ($403291461126605635584000000$ pour être exact). Je vous laisse faire la recherche exhaustive si vous vous voulez, mais moi j’ai envie de trouver une solution avant la fin de l’univers  .
.
Il faut donc trouver mieux que la recherche exhaustive.
L’analyse de fréquences
Petite réflexion : tous les e sont codés par la même lettre, disons f, donc s’il y a plein de e dans le texte initial, il doit y avoir plein de f dans le texte chiffré.
Voici exactement le principe de l’analyse de fréquences. Dans une langue, toutes les lettres n’apparaissent pas à la même fréquence. Par exemple, en français, il y a beaucoup de e, a, i, l, mais peu de x, w ou k. Ainsi, il suffit de déterminer la fréquence des lettres dans le texte final, et en comparant avec les fréquences moyennes d’apparition, on devra pouvoir trouver directement la substitution. Seulement, comme on ne pourra pas vraiment déterminer les lettres ayant de faibles probabilités (pas assez d’occurrences pour avoir une moyenne significative), on utilisera ce procédé sur les lettres à fortes probabilités, et on finira à la main.
Cela ne fonctionne pas si le texte est trop court, car on a alors pas assez de lettres pour avoir des moyennes significatives. Imaginez une phrase comme celle-ci : Chez le vieux zinzin, vous buvez du whisky, il y a beaucoup trop de lettre rares, et ça pourrit complètement l’analyse de fréquences.
Comme les fréquences des lettres changent en fonction de la langue (il y aura par exemple beaucoup plus de w en anglais qu’en français), on admet que l’on chiffre des messages en français.
Voici une table des fréquences en français :
| Lettre : | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fréquence : | 7.9 | 0.8 | 3.2 | 3.2 | 18.2 | 1.0 | 1.0 | 0.8 | 7.2 | 0.3 | 0.0 | 5.7 | 3.0 | 7.6 | 5.6 | 3.1 | 1.0 | 6.8 | 8.5 | 7.0 | 6.2 | 1.2 | 0.0 | 0.4 | 0.3 | 0.1 |
On peut trouver plusieurs distributions de fréquences différentes si l’on se base sur des corpus différents. Celle-ci se base sur des textes littéraires, et elle est donc très différente de celle de Wikipédia. Ce n’est pas trop grave, car de toute façon on va se baser sur la forme générale du diagramme et pas les détails.
Maintenant, si on a un texte chiffré par substitution, il suffira de déterminer les fréquences des lettres et d’essayer de les faire coïncider avec les fréquences de référence en français.
Autres outils de la langue
En théorie, si le texte est assez long, l’analyse de fréquences suffit (pour peu que l’on ait la bonne langue). Cependant, si le texte est un peu court, ou bien s’il est biscornu avec des mots étranges (si c’est un poème sur le whisky par exemple), il faut ruser. Dans ce cas, l’analyse de fréquences ne suffit pas pour déterminer la substitution. On peut alors s’appuyer sur d’autres spécificités de la langue.
Ces outils peuvent également servir à vérifier si la substitution que l’on a trouvé semble juste.
Les doublés
S’il y a deux fois la même lettre juxtaposée, comme dans colle, appel, etc…, alors cette lettre redoublée sera très probablement t, l, n, e, m, p, r ou s.
Par exemple, s’il y a plusieurs doublés de k dans le texte chiffré, et que notre analyse de fréquence dit que k -> c, vous vous êtes probablement plantés.
Les voyelles
Après deux ou trois consonnes, il viendra presque toujours une voyelle. Ca peut être pratique si l’on dispose de consonnes et pas de voyelles.
Les mots courts
Les mots d’une ou deux lettres peuvent aider. Cela nécessite bien entendu d’avoir la ponctuation. Dans ce cas, en français, les mots d’une lettre seront y, a, soit avec un apostrophe comme s’, l’, …
Les mots de deux lettres sont également restreints. Si par exemple, on a e?, ce peut être eh, en, es, et, eu, ou ex, et c’est tout.
Les singularités linguistiques
On peut avoir d’autres outils, comme le q. Il se trouve qu’en français, le q est toujours suivi d’un u, sauf dans cinq, coq, et quelques autres exceptions. Cela peut donc occasionnellement nous servir à trouver le q ou/et le u.
Exemple :
Texte chiffré :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | p iyqqy eyndy hn ay uysiyjupzs pggdyjudy ly kyjn, ly uzjyd yqpzq uyap ihkkyjiy, yq tdpjihzsy, ihkkpjupjq pnc thdiys uy lp jpqndy uybyjnys sys pzuys, ihkky upjs lys tyydzys hn lys rypjqs sy thjq yjrpryd ihkky inzszjzyds, tdpggpzq lp ehnzlly, uhjjpzq p lp bpgynd uys ghkkys uy qyddy p yqnbyd yq tpzspzq tzjzd p ghzjq gpd ly tyn lys ieyts u’hynbdy inlzjpzdys u’pohdu gdygpdys upjs uys dyizgzyjqs uy iydpkzsqys fnz pllpzyjq uys rdpjuys inbys, kpdkzqys, iepnudhjs yq ghzsshjjzydys, pnc qyddzjys ghnd ly rzozyd, khnlys p gpqzssydzy, yq gyqzqs ghqs uy idyky yj gpsspjq gpd njy ihllyiqzhj ihkglyqy uy ipssydhly uy qhnqys uzkyjszhjs. ay k’pddyqpzs p bhzd snd lp qpoly, hn lp tzlly uy inzszjy byjpzq uy lys yihssyd, lys gyqzqs ghzs plzrjys yq jhkodys ihkky uys ozllys bydqys upjs nj ayn ; kpzs khj dpbzssykyjq yqpzq uybpjq lys psgydrys, qdykgyys u’hnqdy-kyd yq uy dhsy yq uhjq l’ygz, tzjykyjq gzrjhiey uy kpnby yq u’pwnd, sy uyrdpuy zjsyjszolykyjq ansfn’pn gzyu – yjihdy shnzlly ghndqpjq un shl uy lynd glpjq – gpd uys zdzspqzhjs fnz jy shjq gps uy lp qyddy. zl ky sykolpzq fny iys jnpjiys iylysqys qdpezsspzyjq lys uylzizynsys idypqndys fnz s’yqpzyjq pknsyys p sy kyqpkhdgehsyd yj lyrnkys yq fnz, p qdpbyds ly uyrnzsykyjq uy lynd iepzd ihkysqzoly yq tydky, lpzsspzyjq pgydiybhzd yj iys ihnlynds jpzsspjqys u’pndhdy, yj iys yopnieys u’pdi-yj-izyl, yj iyqqy ycqzjiqzhj uy shzds olyns, iyqqy yssyjiy gdyizynsy fny ay dyihjjpzsspzs yjihdy fnpju, qhnqy lp jnzq fnz snzbpzq nj uzjyd hn a’yj pbpzs kpjry, yllys ahnpzyjq, upjs lynds tpdiys ghyqzfnys yq rdhsszydys ihkky njy tyydzy uy sepmysgypdy, p iepjryd khj ghq uy iepkody yj nj bpsy uy gpdtnk |
Si l’on compte les lettres de ce texte chiffré (via un programme, parce que ça commence à faire un peu longuet à la main), on obtient la distribution suivante :
| Lettre : | a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fréquence : | 0,48 | 0,97 | 0,18 | 5,32 | 0,73 | 0,6 | 2,24 | 3,75 | 3,08 | 5,32 | 2,72 | 3,38 | 0,06 | 4,11 | 0,66 | 6,4 | 5,2 | 0,85 | 8,1 | 0,91 | 3,32 | 0 | 0,06 | 0 | 15,53 | 5,61 |
On va ensuite tenter au mieux de faire coïncider cette distributions avec celle de la langue française.
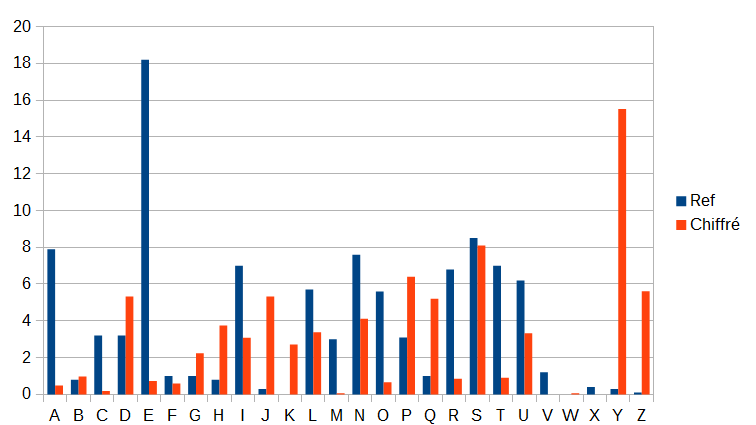
En regardant les lettres qui ont la plus grande fréquence, on voit clairement que le y représente le e. On obtient :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | _ _e__e _e__e __ _e _e__e_____ ____e___e _e _e__, _e ___e_ e____ _e__ ____e__e, e_ ________e, __________ ___ ____e_ _e __ _____e _e_e__e_ _e_ ___e_, ____e ____ _e_ _ee__e_ __ _e_ _e____ _e ____ e____e_ ____e _______e__, ________ __ ______e, _______ _ __ ___e__ _e_ ____e_ _e _e__e _ e___e_ e_ _______ _____ _ _____ ___ _e _e_ _e_ __e__ _’_e___e ________e_ _’_____ __e___e_ ____ _e_ _e____e___ _e _e______e_ ___ _____e__ _e_ _____e_ ___e_, ______e_, _________ e_ _________e_e_, ___ _e____e_ ____ _e ____e_, ____e_ _ ______e__e, e_ _e____ ____ _e __e_e e_ _______ ___ __e ____e_____ _____e_e _e ____e___e _e ____e_ ___e______. _e _’___e____ _ ____ ___ __ ____e, __ __ ____e _e ______e _e____ _e _e_ e____e_, _e_ _e____ ____ _____e_ e_ _____e_ ____e _e_ ____e_ _e__e_ ____ __ _e_ ; ____ ___ ______e_e__ e____ _e____ _e_ ___e__e_, __e__ee_ _’____e-_e_ e_ _e ___e e_ ____ _’e__, ___e_e__ _______e _e ____e e_ _’____, _e _e____e ___e_____e_e__ _____’__ __e_ – e____e ______e ________ __ ___ _e _e__ _____ – ___ _e_ __________ ___ _e ____ ___ _e __ _e__e. __ _e _e______ __e _e_ _____e_ _e_e__e_ _________e__ _e_ _e____e__e_ __e____e_ ___ _’e___e__ ____ee_ _ _e _e_________e_ e_ _e___e_ e_ ___, _ ____e__ _e _e____e_e__ _e _e__ _____ ___e_____e e_ _e__e, _______e__ __e__e____ e_ _e_ ____e___ ________e_ _’_____e, e_ _e_ e_____e_ _’___-e_-__e_, e_ _e__e e_________ _e _____ __e__, _e__e e__e__e __e__e__e __e _e _e___________ e____e _____, ____e __ ____ ___ _______ __ ___e_ __ _’e_ _____ ____e, e__e_ _____e__, ____ _e___ ____e_ __e____e_ e_ ______e_e_ ____e __e _ee__e _e ____e__e__e, _ _____e_ ___ ___ _e ______e e_ __ ___e _e ______ |
Maintenant, on regarde la deuxième lettre ayant la plus grande fréquence. On va donc tenter le s -> s, comme le suggère le diagramme.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | _ _e__e _e__e __ _e _es_e____s ____e___e _e _e__, _e ___e_ e____ _e__ ____e__e, e_ _______se, __________ ___ ____es _e __ _____e _e_e__es ses ___es, ____e ___s _es _ee__es __ _es _e___s se ____ e____e_ ____e ___s___e_s, ________ __ ______e, _______ _ __ ___e__ _es ____es _e _e__e _ e___e_ e_ ___s___ _____ _ _____ ___ _e _e_ _es __e_s _’_e___e ________es _’_____ __e___es ___s _es _e____e__s _e _e____s_es ___ _____e__ _es _____es ___es, ______es, ________s e_ ___ss____e_es, ___ _e____es ____ _e ____e_, ____es _ ____sse__e, e_ _e___s ___s _e __e_e e_ __ss___ ___ __e ____e_____ _____e_e _e __sse___e _e ____es ___e_s___s. _e _’___e___s _ ____ s__ __ ____e, __ __ ____e _e ___s__e _e____ _e _es e__sse_, _es _e___s ___s _____es e_ _____es ____e _es ____es _e__es ___s __ _e_ ; ___s ___ ____sse_e__ e____ _e____ _es _s_e__es, __e__ees _’____e-_e_ e_ _e __se e_ ____ _’e__, ___e_e__ _______e _e ____e e_ _’____, se _e____e __se_s___e_e__ __s__’__ __e_ – e____e s_____e ________ __ s__ _e _e__ _____ – ___ _es ___s_____s ___ _e s___ __s _e __ _e__e. __ _e se______ __e _es _____es _e_es_es _____ss__e__ _es _e____e_ses __e____es ___ s’e___e__ ___sees _ se _e________se_ e_ _e___es e_ ___, _ ____e_s _e _e___se_e__ _e _e__ _____ ___es____e e_ _e__e, ___ss__e__ __e__e____ e_ _es ____e__s ___ss___es _’_____e, e_ _es e_____es _’___-e_-__e_, e_ _e__e e_________ _e s___s __e_s, _e__e esse__e __e__e_se __e _e _e______ss__s e____e _____, ____e __ ____ ___ s______ __ ___e_ __ _’e_ ____s ____e, e__es _____e__, ___s _e__s ____es __e____es e_ ___ss_e_es ____e __e _ee__e _e s___es_e__e, _ _____e_ ___ ___ _e ______e e_ __ __se _e ______ |
Pas mal de double s, ça semble engageant.
Tentons p -> a
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | a _e__e _e__e __ _e _es_e__a_s a___e___e _e _e__, _e ___e_ e_a__ _e_a ____e__e, e_ __a____se, ____a__a__ a__ ____es _e _a _a___e _e_e__es ses a__es, ____e _a_s _es _ee__es __ _es _ea__s se ____ e__a_e_ ____e ___s___e_s, __a__a__ _a ______e, ____a__ a _a _a_e__ _es ____es _e _e__e a e___e_ e_ _a_sa__ _____ a _____ _a_ _e _e_ _es __e_s _’_e___e _____a__es _’a____ __e_a_es _a_s _es _e____e__s _e _e_a__s_es ___ a__a_e__ _es __a__es ___es, _a____es, __a_____s e_ ___ss____e_es, a__ _e____es ____ _e ____e_, ____es a _a__sse__e, e_ _e___s ___s _e __e_e e_ _assa__ _a_ __e ____e_____ _____e_e _e _asse___e _e ____es ___e_s___s. _e _’a__e_a_s a ____ s__ _a _a__e, __ _a ____e _e ___s__e _e_a__ _e _es e__sse_, _es _e___s ___s a____es e_ _____es ____e _es ____es _e__es _a_s __ _e_ ; _a_s ___ _a__sse_e__ e_a__ _e_a__ _es as_e__es, __e__ees _’____e-_e_ e_ _e __se e_ ____ _’e__, ___e_e__ _______e _e _a__e e_ _’a___, se _e__a_e __se_s___e_e__ __s__’a_ __e_ – e____e s_____e _____a__ __ s__ _e _e__ __a__ – _a_ _es ___sa____s ___ _e s___ _as _e _a _e__e. __ _e se___a__ __e _es __a__es _e_es_es __a__ssa_e__ _es _e____e_ses __ea___es ___ s’e_a_e__ a__sees a se _e_a______se_ e_ _e___es e_ ___, a __a_e_s _e _e___se_e__ _e _e__ __a__ ___es____e e_ _e__e, _a_ssa_e__ a_e__e____ e_ _es ____e__s _a_ssa__es _’a____e, e_ _es e_a___es _’a__-e_-__e_, e_ _e__e e_________ _e s___s __e_s, _e__e esse__e __e__e_se __e _e _e____a_ssa_s e____e __a__, ____e _a ____ ___ s___a__ __ ___e_ __ _’e_ a_a_s _a__e, e__es ___a_e__, _a_s _e__s _a__es __e____es e_ ___ss_e_es ____e __e _ee__e _e s_a_es_ea_e, a __a__e_ ___ ___ _e __a___e e_ __ _ase _e _a____ |
Le premier mot est un mot d’une lettre et c’est un a : on a l’air d’être sur la bonne piste.
Maintenant, on a z, j, d qui ont des grandes probabilités. Ces lettres donneront sûrement i, n, et t. Malheureusement, on ne sais pas exactement qui va où. Il faut donc tenter, et si ça ne fonctionne pas, on reviendra en arrière.
Testons z -> i
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | a _e__e _e__e __ _e _es_e__ais a___e___e _e _e__, _e _i_e_ e_ai_ _e_a ____e__e, e_ __a___ise, ____a__a__ a__ ____es _e _a _a___e _e_e__es ses ai_es, ____e _a_s _es _ee_ies __ _es _ea__s se ____ e__a_e_ ____e __isi_ie_s, __a__ai_ _a ___i__e, ____ai_ a _a _a_e__ _es ____es _e _e__e a e___e_ e_ _aisai_ _i_i_ a __i__ _a_ _e _e_ _es __e_s _’_e___e ___i_ai_es _’a____ __e_a_es _a_s _es _e_i_ie__s _e _e_a_is_es __i a__aie__ _es __a__es ___es, _a__i_es, __a_____s e_ __iss___ie_es, a__ _e__i_es ____ _e _i_ie_, ____es a _a_isse_ie, e_ _e_i_s ___s _e __e_e e_ _assa__ _a_ __e ____e__i__ _____e_e _e _asse___e _e ____es _i_e_si__s. _e _’a__e_ais a __i_ s__ _a _a__e, __ _a _i__e _e __isi_e _e_ai_ _e _es e__sse_, _es _e_i_s __is a_i__es e_ _____es ____e _es _i__es _e__es _a_s __ _e_ ; _ais ___ _a_isse_e__ e_ai_ _e_a__ _es as_e__es, __e__ees _’____e-_e_ e_ _e __se e_ ____ _’e_i, _i_e_e__ _i_____e _e _a__e e_ _’a___, se _e__a_e i_se_si__e_e__ __s__’a_ _ie_ – e____e s__i__e _____a__ __ s__ _e _e__ __a__ – _a_ _es i_isa_i__s __i _e s___ _as _e _a _e__e. i_ _e se___ai_ __e _es __a__es _e_es_es __a_issaie__ _es _e_i_ie_ses __ea___es __i s’e_aie__ a__sees a se _e_a______se_ e_ _e___es e_ __i, a __a_e_s _e _e__ise_e__ _e _e__ __ai_ ___es_i__e e_ _e__e, _aissaie__ a_e__e__i_ e_ _es ____e__s _aissa__es _’a____e, e_ _es e_a___es _’a__-e_-_ie_, e_ _e__e e__i___i__ _e s_i_s __e_s, _e__e esse__e __e_ie_se __e _e _e____aissais e____e __a__, ____e _a __i_ __i s_i_ai_ __ _i_e_ __ _’e_ a_ais _a__e, e__es ___aie__, _a_s _e__s _a__es __e_i__es e_ ___ssie_es ____e __e _ee_ie _e s_a_es_ea_e, a __a__e_ ___ ___ _e __a___e e_ __ _ase _e _a____ |
On commence à avoir des bouts de mots comme -aissais qui ressemblent à quelque chose. On est donc certainement sur la bonne piste.
L’un des deux entre d et j devrait donner n. Tentons d -> n.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | a _e__e _e_ne __ _e _es_e__ais a__ne__ne _e _e__, _e _i_en e_ai_ _e_a ____e__e, e_ _na___ise, ____a__a__ a__ __n_es _e _a _a__ne _e_e__es ses ai_es, ____e _a_s _es _eenies __ _es _ea__s se ____ e__a_en ____e __isi_iens, _na__ai_ _a ___i__e, ____ai_ a _a _a_e_n _es ____es _e _enne a e___en e_ _aisai_ _i_in a __i__ _an _e _e_ _es __e_s _’_e__ne ___i_aines _’a__n_ _ne_anes _a_s _es ne_i_ie__s _e _ena_is_es __i a__aie__ _es _na__es ___es, _an_i_es, __a__n__s e_ __iss___ienes, a__ _enni_es ___n _e _i_ien, ____es a _a_issenie, e_ _e_i_s ___s _e _ne_e e_ _assa__ _an __e ____e__i__ _____e_e _e _assen__e _e ____es _i_e_si__s. _e _’anne_ais a __in s_n _a _a__e, __ _a _i__e _e __isi_e _e_ai_ _e _es e__ssen, _es _e_i_s __is a_i__es e_ ____nes ____e _es _i__es _en_es _a_s __ _e_ ; _ais ___ na_isse_e__ e_ai_ _e_a__ _es as_en_es, _ne__ees _’___ne-_en e_ _e n_se e_ ____ _’e_i, _i_e_e__ _i_____e _e _a__e e_ _’a__n, se _e_na_e i_se_si__e_e__ __s__’a_ _ie_ – e___ne s__i__e ___n_a__ __ s__ _e _e_n __a__ – _an _es inisa_i__s __i _e s___ _as _e _a _enne. i_ _e se___ai_ __e _es __a__es _e_es_es _na_issaie__ _es _e_i_ie_ses _nea__nes __i s’e_aie__ a__sees a se _e_a__n___sen e_ _e___es e_ __i, a _na_ens _e _e__ise_e__ _e _e_n __ain ___es_i__e e_ _en_e, _aissaie__ a_en_e__in e_ _es ____e_ns _aissa__es _’a_n_ne, e_ _es e_a___es _’an_-e_-_ie_, e_ _e__e e__i___i__ _e s_ins __e_s, _e__e esse__e _ne_ie_se __e _e ne____aissais e___ne __a__, ____e _a __i_ __i s_i_ai_ __ _i_en __ _’e_ a_ais _a__e, e__es ___aie__, _a_s _e_ns _an_es __e_i__es e_ _n_ssienes ____e __e _eenie _e s_a_es_eane, a __a__en ___ ___ _e __a__ne e_ __ _ase _e _an___ |
Quelques trucs paraissent louches : anne_ais, _a_issenie. Dans le doute, on va tester j -> n.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | a _e__e _e__e __ _e _es_en_ais a___en__e _e _en_, _e _ine_ e_ai_ _e_a ____en_e, e_ __an__ise, ____an_an_ a__ ____es _e _a na___e _e_en_es ses ai_es, ____e _ans _es _ee_ies __ _es _ean_s se __n_ en_a_e_ ____e __isinie_s, __a__ai_ _a ___i__e, __nnai_ a _a _a_e__ _es ____es _e _e__e a e___e_ e_ _aisai_ _ini_ a __in_ _a_ _e _e_ _es __e_s _’_e___e ___inai_es _’a____ __e_a_es _ans _es _e_i_ien_s _e _e_a_is_es __i a__aien_ _es __an_es ___es, _a__i_es, __a____ns e_ __iss_nnie_es, a__ _e__ines ____ _e _i_ie_, ____es a _a_isse_ie, e_ _e_i_s ___s _e __e_e en _assan_ _a_ _ne ____e__i_n _____e_e _e _asse___e _e ____es _i_ensi_ns. _e _’a__e_ais a __i_ s__ _a _a__e, __ _a _i__e _e __isine _enai_ _e _es e__sse_, _es _e_i_s __is a_i_nes e_ n____es ____e _es _i__es _e__es _ans _n _e_ ; _ais __n _a_isse_en_ e_ai_ _e_an_ _es as_e__es, __e__ees _’____e-_e_ e_ _e __se e_ __n_ _’e_i, _ine_en_ _i_n___e _e _a__e e_ _’a___, se _e__a_e insensi__e_en_ __s__’a_ _ie_ – en___e s__i__e _____an_ __ s__ _e _e__ __an_ – _a_ _es i_isa_i_ns __i ne s_n_ _as _e _a _e__e. i_ _e se___ai_ __e _es n_an_es _e_es_es __a_issaien_ _es _e_i_ie_ses __ea___es __i s’e_aien_ a__sees a se _e_a______se_ en _e___es e_ __i, a __a_e_s _e _e__ise_en_ _e _e__ __ai_ ___es_i__e e_ _e__e, _aissaien_ a_e__e__i_ en _es ____e__s naissan_es _’a____e, en _es e_a___es _’a__-en-_ie_, en _e__e e__in__i_n _e s_i_s __e_s, _e__e essen_e __e_ie_se __e _e _e__nnaissais en___e __an_, ____e _a n_i_ __i s_i_ai_ _n _ine_ __ _’en a_ais _an_e, e__es ___aien_, _ans _e__s _a__es __e_i__es e_ ___ssie_es ____e _ne _ee_ie _e s_a_es_ea_e, a __an_e_ __n ___ _e __a___e en _n _ase _e _a____ |
Il y a du mieux : pas de choses étranges, et des mots presque entier : naissan_es (naissances ?), insensi__e_en_ (insensiblement ?).
En fait, maintenant, on a fait le plus difficile. Il ne reste plus qu’à trouver les « petites lettres » en devinant des mots. Si on ne sait pas, on continue d’utiliser les fréquences. On finit par obtenir :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | a cette heure ou je descendais apprendre le menu, le diner etait deja commence, et francoise, commandant aux forces de la nature devenues ses aides, comme dans les feeries ou les geants se font engager comme cuisiniers, frappait la houille, donnait a la vapeur des pommes de terre a etuver et faisait finir a point par le feu les chefs d’oeuvre culinaires d’abord prepares dans des recipients de ceramistes qui allaient des grandes cuves, marmites, chaudrons et poissonnieres, aux terrines pour le gibier, moules a patisserie, et petits pots de creme en passant par une collection complete de casserole de toutes dimensions. je m’arretais a voir sur la table, ou la fille de cuisine venait de les ecosser, les petits pois alignes et nombres comme des billes vertes dans un jeu ; mais mon ravissement etait devant les asperges, trempees d’outre-mer et de rose et dont l’epi, finement pignoche de mauve et d’azur, se degrade insensiblement jusqu’au pied – encore souille pourtant du sol de leur plant – par des irisations qui ne sont pas de la terre. il me semblait que ces nuances celestes trahissaient les delicieuses creatures qui s’etaient amusees a se metamorphoser en legumes et qui, a travers le deguisement de leur chair comestible et ferme, laissaient apercevoir en ces couleurs naissantes d’aurore, en ces ebauches d’arc-en-ciel, en cette extinction de soirs bleus, cette essence precieuse que je reconnaissais encore quand, toute la nuit qui suivait un diner ou j’en avais mange, elles jouaient, dans leurs farces poetiques et grossieres comme une feerie de shakespeare, a changer mon pot de chambre en un vase de parfum |
Bon c’est pas le texte qui compte bien sûr (parce que là c’est du Proust  , un extrait random de « Du côté de chez Swann »), mais la méthode.
, un extrait random de « Du côté de chez Swann »), mais la méthode.
On procède de la même manière si l’on n’a pas de la ponctuation. Seulement, c’est plus compliqué car il y a plusieurs outils de vérification qui ne sont pas à notre disposition (mots de 1 et 2 lettres par exemple).
Une méthode un peu plus générale
Là, on l’a fait en mode barbare symérien1, en tenant des lettres comme un bourrin et en avançant pas à pas. On peut le faire de manière un peu plus automatique en demandant à l’ordinateur de tester plusieurs permutations, comme dans le cas de la recherche exhaustive, mais en restreignant les cas. Par exemple, on teste toutes les permutations telles que :
- la lettre de fréquence maximale sera un e
- les 4 lettres suivantes seront s, a, n, i
- les 2 suivantes seront t, r
- les 3 suivantes seront u, o, l
- les 4 suivantes seront c, d, m, p
- le reste, on s’en tamponne l’oreille avec une babouche !
Il y a donc $(4*3*2)*(2)*(3*2)*(4*3*2) = 6912$ possibilités à tester. C’est mieux que les $403291461126605635584000000$ de tout à l’heure quand même  . Et puis on peut même commencer sans les 4 dernières lettres : seulement $144$ possibilités ! Après, on peut souvent finir à la main sans trop de problèmes.
. Et puis on peut même commencer sans les 4 dernières lettres : seulement $144$ possibilités ! Après, on peut souvent finir à la main sans trop de problèmes.
Bon, les substitutions monoalphabétiques, on sait faire maintenant. Sachez qu’il y a quantité de méthodes utilisant la substitution : carré de Polybe, chiffre de Delastelle, chiffre des Templiers, chiffre de PigPen, chiffres hébreux, chiffre de Wolseley, hommes dansants, la ligne du bas dans Artémis Fowl2 (oui je me suis amusé à déchiffrer ces trucs  et par ailleurs, c’est un très bon moyen de s’entraîner), et j’en passe.
et par ailleurs, c’est un très bon moyen de s’entraîner), et j’en passe.
Conclusion : vous savez déchiffrer tout ça !
-
Ecoutez reflets d’acide, vous ne serez pas déçus. ↩
-
Excellents livres (je conseille fortement les tomes 1-4). ↩
L'analyse de bigrammes
Reprenons l’exemple du texte précédent, chiffré avec une autre méthode
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | UZUIR ENWAW AZUSI AQBUX LTSPS XZJZU LTZUX QGVBI XQTEP AZUBC ECDCP EIPMZ WSUXU IVZMY IPAVE TEJQT LTMYB CYMJE RGQBD CHOZY DMZUD CJOBI QBIZS XSUQB IPMZI AMYKW QBVMM UWBWR CGQBE RMYVY IZJEX BWSOP ERRGE JGVGF AVGMW BDOVZ UMRIE CHOBO QLZNI AIQZY ECEKS CUMYP VNQBV CMZQB DCREZ HWFUI QYMUU IFKAV SPVLG MWOUM OHXBR IBRQO YPXQA LNWZG RUYPJ BETCG GMSPZ UESQS YSVBZ URIZU ESMYE SQBZU KZXMW SVYDC UXJSW XQAQB CXGZZ NSPWS NXQBE EMYDC ALQYQ BQTFY ECQBG SOVDP IQIZJ DOHMT IQFCM UQBOV JZMUP WPAAY KNBRU VKGWB FYKNX QSXRI HGMTM UWBUI HKHGV YVCVY DCUKS LMHHZ GHSXX BRILC PAIPZ NETHG IQIPY UXQRE DCEVM TMUAC IAUIK NREES CFWSY BIQCI SLCAZ UBCAV SCOHD OAWHO BCNPA ZCGGU YYXQD CGFAV GMCWW SSPNX OEQBE TCZIZ BRQBH KHGVY VCAVE KEPPA IZBPE JLFQB IPMZI AQBBU ZNQBJ OHVQB NATUK UFGGN SPODI QJSZQ MTSLW SREBC ECDCT MXBXQ SXAYM UERQA ZUYUM HESKN RRSLM UUIDC NMIZU IRUXB XQXML OPAGV XBXMO CQRNW DCQTQ YMHNX IEAWI ZDCEE YGCJT UWSYB NPSLW SLNED CXOVX MIAWS IPZUW RQLZN EGKNH VMYNX EDACD CXQAW JHMYJ DCADC YBPWS XHGIQ EFQLP AWRXB RIESO EKOMU ZUYYG VIZUA HOECC XETQB BIMYU XALOE QBREQ AJSDY MTSPW STBQB DCNSK ZYPIZ ALZUK OAWQB CXAVU ISPWS BCSDI ZQBGH SLUII RYSTF CZMUW SXQQZ GVIZN KQLKO JSJOD OXQDC QZAVS LWSNX OEYPR GXUWO IPGVQ AKGXQ UIVMF YOESP MTSPW SBCHK RGCWO HZUHM QBIPC GYPDO ZYAVS XXBQB NAAWY SMHHM QBAMO VGSQB NARGW SKZOE WSUXZ FMHJZ GMCYK TLTQB OHDON PYPAL UIREQ BIZHM EGZUK ZYPIZ CXGQM UETIQ ZYAVS XAVWS IPZUC XMYLD KNREH OBIEC CXAVQ LTMEC KUTEP ANMUS WSSCS PODMY EROEX QCIKN SPWSN XMYKW YPDOF KRGQB VCUIS HAJIZ ZSNMM TWBZU ALEJG VKUQO MHPWI AQBXU OLAYW FZUUZ XUXOM UUNHZ GGDCG SIRLF MHBIF PGHIA EGCAH UEY |
L’analyse de fréquences dans l’ordre croissant donne :
| Lettre | Q | U | S | B | Z | I | C | M | E | A | X | Y | P | W | G | O | V | H | R | N | D | K | L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fréquence (%) | 5.84 | 5.69 | 5.61 | 5.31 | 5.31 | 5.24 | 5.16 | 5.08 | 4.86 | 4.48 | 4.25 | 4.25 | 3.79 | 3.72 | 3.72 | 3.41 | 3.26 | 2.96 | 2.81 | 2.73 | 2.66 | 2.35 | 2.28 |
Ce n’est pas du tout ce que l’on pouvait attendre d’une substitution. Les fréquences sont bien trop rapprochées pour pouvoir distinguer les lettres. Conclusion : il ne s’agit probablement pas d’une substitution monoalphabétique.
Pourtant, il s’agit bien d’une substitution. Seulement, ce n’est pas une substitution sur les lettres, mais sur des bigrammes : le message initial est divisé en paquets de 2 lettres, et chaque paquet est remplacé par un paquet correspondant.
L’analyse de bigrammes
D’une manière similaire à l’analyse de fréquences classique, on peut effectuer l’analyse des bigrammes qui interviennent, et comparer ceux du texte avec ceux de la langue du texte. Regardons alors les bigrammes les plus fréquents dans notre texte :
| Bigramme | QB | WS | DC | ZU | IZ | XQ | UI | SP | MU | MY | AV | IP |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fréquence | 5.01 | 3.03 | 2.73 | 2.73 | 2.12 | 1.97 | 1.97 | 1.82 | 1.82 | 1.82 | 1.82 | 1.52 |
Pour comparer, voici les bigrammes les plus utilisés en français. Encore une fois, ce n’est qu’à titre indicatif car ça dépend du corpus considéré :
| Bigramme | ES | LE | DE | RE | EN | ON | NT | ER | TE | ET | EL | AN | SE |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Fréquence (%) | 3.05 | 2.2 | 2.2 | 2.1 | 2.08 | 1.64 | 1.62 | 1.53 | 1.52 | 1.43 | 1.42 | 1.37 | 1.32 |
Dans les substitutions de bigrammes, l’analyse de bigrammes est l’arme la plus efficace que nous ayons. C’est le cas pour le chiffre de Hill : la clé est une matrice qui chiffre les lettres deux par deux. De la même manière qu’on a cassé les substitutions simples avec l’analyse de fréquences, on peut casser Hill avec l’analyse des bigrammes.
Ici, on peut donc effectuer la même chose qu’avec la substitution classique mais avec les bigrammes. On peut donc supposer que es est codé en qb, et continuer comme ça.
Tout comme l’analyse de fréquences simple, on ne peut tirer des conclusions de l’analyse que s’il y a un nombre significatif de bigrammes.
Par conséquent, l’analyse est plus compliquée, et il faut un texte plus long pour avoir des fréquences plus sûres.
L’analyse des bigrammes peut également aider dans les substitutions monoalphabétiques, comme dans la partie d’avant. Cette analyse permet d’obtenir des informations supplémentaires en cas de doute sur l’analyse simple.
Vigenere et l'indice de coïncidence
Attaquons-nous maintenant à un chiffrage qui a résisté pendant plusieurs siècles : le chiffre de Vigenère. Pour rappeler le principe, il s’agit d’un chiffrement par substitution polyalphabétique. On dispose d’une clé qui représente le décalage à effectuer à chaque caractère.
Exemple
| Message original | Z | E | S | T | E | D | E | S | A | V | O | I | R |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Message original (nombres) | 26 | 5 | 19 | 20 | 5 | 4 | 5 | 19 | 1 | 22 | 15 | 9 | 18 |
| Clé | C | L | E | M | C | L | E | M | C | L | E | M | C |
| Clé (décalage) | 2 | 11 | 4 | 12 | 2 | 11 | 4 | 12 | 2 | 11 | 4 | 12 | 2 |
| Message chiffré (nombre) | 2 | 16 | 23 | 6 | 7 | 15 | 9 | 5 | 3 | 7 | 19 | 21 | 20 |
| Message chiffré | B | P | W | F | G | O | I | E | C | G | S | U | T |
Ainsi, « ZESTEDESAVOIR » chiffré avec la clé « CLEM » donne « BPWFGOIECGSUT ».
En connaissant la longueur de la clé
Si l’on connaît la longueur de la clé, ce n’est pas si compliqué. Disons que la clé est de longueur $k$. Alors, si l’on prend une lettre sur $k$, toutes les lettres sont chiffrées par le même décalage : il s’agit d’une substitution toute simple comme nous en avons déjà fait.
On a donc simplement à déchiffrer $k$ substitutions pour obtenir le bon message !
Comme d’habitude, il faut avoir suffisamment de lettres pour obtenir des analyses de fréquences probantes.
Le gros problème est donc d’obtenir la longueur de la clé. Il existe pour cela plusieurs techniques. Nous allons nous intéresser à l’indice de coïncidence.
Indice de coïncidence
L’indice de coïncidence peut en premier lieu servir à savoir si un texte a été chiffré avec une substitution monoalphabétique ou polyalphabétique en étudiant toujours la fréquence des lettres. Le principe est le même qu’au dessus : regarder si les lettres ont des fréquences semblables à celles de la langue concernée ou pas.
L’indice de coïncidence est défini par : $IC = \sum_{q=A}^{q=Z} \dfrac{n_q(n_q-1)}{n(n-1)}$ avec $n$ le nombre total de lettres du message, $n_A$ le nombre de « A », $n_B$ le nombre de « B », …
Dans le cas d’un texte aléatoire (d’une distribution aléatoire, où toutes les lettres ont donc la même fréquence), on obtient $0,0385$. Si l’on prend un texte de la langue française, on obtient un indice aux alentours de $0,0746$.
Ainsi, si l’on trouve un indice de coïncidence proche de $0.0746$, il s’agit très certainement d’une substitution. Au contraire, si l’on a un indice proche de $0.0385$, ce n’est probablement pas une substitution, mais quelque chose de plus complexe.
Trouver la longueur de la clé
Une fois que l’on a déterminé que notre texte chiffré était bien une substitution polyalphabétique, on aimerait bien déterminer la longueur de la clé pour pouvoir déchiffrer le message.
Pour tester si la clé est de longueur $k$ :
- à partir du texte chiffré, on créé $k$ nouveaux textes en prenant une lettre sur $k$ à chaque fois.
- on détermine l’indice de coïncidence pour chaque texte.
- si les indices sont en moyenne bien plus proches de l’indice de la langue que l’indice moyen, on a sûrement la bonne longueur de la clé.
Exemple de la méthode
Si l’on a le texte chiffré « abcdefghijklmnopqrstuvwxyz » (passionnant n’est-il pas ?) pour tester une clé de longueur 5, alors la première étape donnera 5 textes en prenant à chaque fois une lettre sur 5 :
- afkpuz
- bglqv
- chmrw
- dinsx
- ejoty
et on fait le test de l’indice de coïncidence sur ces textes.
En effet, si la clé est bien de longueur 5, alors chacun de ces textes est en fait un chiffrement par décalage, et l’indice de coïncidence est proche de celui de la langue. Sinon, chacun de ces textes est un texte chiffré avec un décalage variable, et donc on a un indice de coïncidence proche de l’aléatoire.
On fait ces opérations pour toutes les longueurs de clé, et on compare pour déterminer quelle est la longueur de clé la plus probable.
Exemple :
Prenons un texte chiffré. Tentons de déterminer la longueur de la clé :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | HCVEX LHVFV LOLUI KEJNI UDRTW HPGCI UDIPP LMVYY SEUTR LRVEE PTUPN HCFXQ LNTPI AFILR JOZDI JODXE UDRYX HUOQS YCVDH LLRYE AUIPH LVVYY LSJPW HIUPW JODXI KAEDP LSWPI YIVDS BLVDK LAEEW ZEWZR AEERE NEINS TMVNY PSZYM LRJQV HPGLM ALRSS BICWI KOEYE PTRWE CAGPY YDVDT VMDPW KEKPV YERPX BVVCI AFRTW HIKQM UIILT VIEET HRCPJ LUCPW JHVQW KOVFZ YETFP PNRTV LSULF VRUAV LPRCI ZDRYW KEJCI JIGTI UTJOI JEILQ PSKPW XUZLP SAZPR ADVDK YAEOI ZCLGI ZMRCQ PTVDG OALOV VNJPX WOZDW VNETI YEJLY ETVCV PNVDT VUIWI NISTI YMFFP LSRAE AIJDI YIVPX WEKTX ZPFEW KETCI TEVYT HSJLR APRCY UETZP SETEM VNTZQ WLVEI KETLW ZEIZP LDVES BTVDH PMVYW POEDN LMRCV LTRTW HVFTV ZUIWE AASWI VUCLJ PLCPH LCLTW PNVGI UAZEH LLVDI JOJDI YLVDT LTZEW WOZDE SIXYI ZEKYS TBIPW JODXI KEJMM SLVDZ LRKPW KAEDY UJVFQ HIJXS URRGM ZSVXI UTVEE PTUPZ HNKWI ZAJAI YGVDX YEDAI LSUZY ARVXI YEKOI YOJPI ADFYX SEGTJ PNVXI UTGTK UOTSI KEDLY CEVEH HZLCW LDVRV HDVTR ZEEDM ILVXI UTAFW XURFT PEUPR JOIPW VUZWP LPFFV AAEEH BSFWH LLVFV WLRYX WAIOI ZIITW HTZZR ZQLTR LSFYX WAJOI SAKPV YEZWQ LSVXF SAZEU BETPW UURYG LSTPP LSKPW ARRSM ZSRTI UTCPW KECTG PELDI ZCIPE AUIPW XUZDI AAZPR AADFW LEJLW LMVEE TOIAL VSVCI ULVRY TEJPX XUZLX YAMPV ZLVOI NUZDI TEEEH LLVFV JHRTV JODPW AISWI LTWPV TECLM ZSRTI UTRAI YCVGS PRVYG LSTZY SELCW UAZDW HNKPW KALCS YEVYG LSVME BCYPW KAINI UCZPP LNTPX AEVIX PNTEM VNUPW VIIDF SELDG LTKPI ZSVYG LPIPG PELDI XUVUI YETZR UAZDW HIJPR JOIPU BAEOX VUKPP HNLTX XUZDY PVRTX BNUTR LRFFN LNRGE PSDLR NEVWP LSAZY HIVYX KAEDP LUIDJ HRTPW WOVEM XUVDI AGIZW ZIVCI ZCFXQ LUEPJ LEITI KEJSE REJAI HRVLG OAERI YMFYT VTUPG OADMV LEEFR CAJPH LPRCJ BM |
Si l’on tente de déterminer son indice de coïncidence, on obtient : 0.0477. Ce n’est donc très probablement pas une substitution simple.
C’est donc peut-être du Vigenère (d’autant plus qu’on est dans la section Vigenère  ).
).
Le fait que le texte soit scindé en paquets de 5 lettres ne signifie pas que la clé soit de longueur 5. En cryptographie, comme la ponctuation est souvent négligée, on ne transmet que les lettres et pour plus de clarté on les sépare en paquets (5 ici).
Faisons donc une analyse des indices de coïncidences pour les différentes longueurs de clé (on va supposer que la clé n’a pas une longueur supérieure à 25).
Testons le cas $k = 3$
Premier texte
1 2 3 4 5 6 | HEHVLKNDWGUPMYULETNFLPFRZJXDXOYDLEILYSWUJXAPWYDLKEZZEEITNSMJHLLSCKYTEGYDMWKYPVIRH QITEHPUWVKFEPRLLRVRZYEIGUOEQKXLARVYOCIRPDAVJWDNIJECNTINTMPRADIXKZEEIVHLPYTSENQVKL EPVBDMWELCTWFZWAICPPCWVUELIJYDTWZSYESIJXEMVLPAYVHXRMVUETZKZAGXDLZRIKYPDXGPXTKTKLE HLLRDREIXTWRPPOWZLFAHFLFLXIZTTRLLYAIKYWSFZBPUGTLPRMRUPEGLZPUWZAPAWJLEOLVUREXZYPLI ZTELVRJPIIWTLSIRYGRGTSCAWKKCEGVBPAIZLPEXTVPIFLLPSGIPDUITUDIRIBOUPLXDVXULFNEDNWSYV KDUJTWEUIIZCCQELTEEJHLAIFVPAVECPPJ |
Indice de coïncidence : 0.0474
Deuxième texte
1 2 3 4 5 6 | CXVLUEIRHCDPVSTREUHXNIIJDOERHQCHRAPVYJHPOIELPISVLEERENNMYZLQPMRBWOERCPDTDKPEXVATI MIVERJCJQOZTPTSFULCDWJJTTIIPPUPZADAILZCTGLVPOWEYLTVVVWIIFLAIIVWTPWTTYSRRUZEMTWEEW ILETHVPDMVRHTUESVLLHLPGAHVJDLTZWDIIKTPOIJSDRWEUFISRZXTEUHWAIVYASYVYOOIFSTNIGUSEYV HCDVVZDLIAXFERIVWPVEBWLVRWOIWZZTSXJSPEQVSEEWRLPSWRZTTWCPDCEIXDARDLLMEIVCLYJXLAVVN DEHVJTOWSLPEMRUACSVLZEWZHPASVLMCWIUPNXVPENWISDTIVLPEIVYZAWJJPAXKHTUYRBTRNRPLEPAHY APIHPOMVAZIIFLPEIJRARGEYYTGDLFAHRB |
Indice de coïncidence : 0.0493
Troisième texte
1 2 3 4 5 6 | VLFOIJUTPIILYERVPPCQTALOIDUYUSVLYUHVLPIWDKDSIVBDAWWARESVPYRVGASIIEPWAYVVPEVRBCFWK ULITCLPHWVYFNVUVAPIRKCIIJJLSWZSPDKEZGMQVOONXZVTEYVPDUISYFSEJYPEXFKCETJACEPTVZLITZ ZDSVPYONRLTVVIAWUJCLTNIZLDOIVLEOEXZYBWDKMLZKKDJQJUGSIVPPNIJYDEIUAXEIJAYEJVUTOIDCE ZWVHTEMVUFUTUJPUPFAESHVWYAIIHZQRFWOAVZLXAUTUYSPKASSICKTEIIAPUIZAFEWVTASIVTPUXMZOU IELFHVDAWTVCZTTIVPYSYLUDNWLYYSEYKNCPTAINMUVDEGKZYPGLXUERZHPOUEVPNXZPTNRFLGSRVLZIX ELDRWVXDGWVZXUJIKSEIVORMTUOMERJLCM |
Indice de coïncidence : 0.0467
On voit que l’on obtient à chaque fois un indice plus proche de l’indice aléatoire que de l’indice de la langue.
Cas $k = 5$ :
Le premier texte :
1 2 3 4 | HLLKUHULSLPHLAJJUHYLALLHJKLYBLZANTPLHABKPCYVKYBAHUVHLJKYPLVLZKJUJPXSAYZZPOVWVYEPV NYLAYWZKTHAUSVWKZLBPPLLHZAVPLPULJYLWSZTJKSLKUHUZUPHZYYLAYYASPUUKCHLHZIUXPJVLABLWW ZHZLWSYLSBULLAZUKPZAXAALLTVUTXYZNTLJJALTZUYPLSUHKYLBKULAPVVSLZLPXYUHJBVHXPBLLPNLH KLHWXAZZLLKRHOYVOLCLB |
Son indice de coïncidence : 0.0769
Le deuxième texte :
1 2 3 4 | CHOEDPDMERTCNFOODUCLUVSIOASILAEEEMSRPLIOTADMEEVFIIIRUHOENSRPDEITESUADACMTANONETNU IMSIIEPEESPEENLEEDTMOMTVUAULCNALOLTOIEBOELRAJIRSTTNAGESREODENTOEEZDDELTUEOUPASLLA ITQSAAESAEUSSRSTEECUUAAEMOSLEUALUELHOITESTCRSEANAESCACNENNIETSPEUEAIOAUNUVNRNSESI AUROUGICUEEERAMTAEAPM |
Son indice de coïncidence : 0.0783
Le troisième texte :
1 2 3 4 | VVLJRGIVUVUFTIZDROVRIVJUDEWVVEWEIVZJGRCERGVDKRVRKIECCVVTRUURRJGJIKZZVELRVLJZEJVVI SFRJVKFTVJRTTTVTIVVVERRFISCCLVZVJVZZXKIDJVKEVJRVVUKJVDUVKJFGVGTDVLVVEVARUIZFEFVRI IZLFJKZVZTRTKRRCCLIIZZDJVIVVJZMVZEVRDSWCRRVVTLZKLVVYIZTVTUILKVILVTZJIEKLZRUFRDVAV EITVVIVFEIJJVEFUDEJR |
Son indice de coïncidence : 0.0926
Le quatrième texte :
1 2 3 4 | EFUNTCPYTEPXPLDXYQDYPYPPXDPDDEZRNNYQLSWYWPDPPPCTQLEPPQFFTLACYCTOLPLPDOGCDOPDTLCDW TFADPTECYLCZEZELZEDYDCTTWWLPTGEDDDEDYYPXMDPDFXGXEPWADAZXOPYTXTSLECRTDXFFPPWFEWFYO TZTYOPWXEPYPPSTPTDPPDPFLEACRPLPODEFTPWPLTAGYZCDPCYMPNPPIEPDDPYPDUZDPPOPTDTTFGLWZY DDPEDZCXPTSALRYPMFPC |
Son indice de coïncidence : 0.0847
Le cinquième texte :
1 2 3 4 | XVIIWIPYRENQIRIEXSHEHYWWIPISKWRESYMVMSIEEYTWVXIWMTTJWWZPVFVIWIIIQWPRKIIQGVXWIYVTI IPEIXXWITRYPMQIWPSHWNVWVEIJHWIHIITWEISWIMZWYQSMIEZIIXIYIIIXJIKIYHWVRMIWTRWPVHHVXI WRRXIVQFUWGPWMIWGIEWIRWWELIYXXVIIHVVWIVMIISGYWWWSGEWIPXXMWFGIGGIIRWRUXPXYXRNERPYX PJWMIWIQJIEIGITGVRHJ |
Son indice de coïncidence : 0.0937
Même si ces indices ne sont pas tous très proches de l’indice de la langue, ils sont bien plus proches de l’indice de la langue que de l’indice du texte aléatoire.
On fait le même calcul pour toutes les valeurs de $k$ entre $2$ et $25$, et on obtient les valeurs moyennes suivantes :
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.048 | 0.048 | 0.048 | 0.048 | 0.085 | 0.047 | 0.047 | 0.047 | 0.047 | 0.085 | 0.048 | 0.047 | 0.047 | 0.046 | 0.086 | 0.047 | 0.046 | 0.046 | 0.049 | 0.085 | 0.046 | 0.047 | 0.047 | 0.047 | 0.084 |
En faisant un peu de tri dans ces valeurs, on remarque qu’elles sont toutes entre 0.046 et 0.049 sauf pour 5, 10, 15, 20 et 25.
La clé est donc très probablement de taille 5. C’est tout à fait normal que les multiples de 5 semblent fonctionner aussi car lors du test avec les indices de coïncidence, prendre une lettre sur 10 ou 15 donne la même distribution qu’une lettre sur 5, et donc à peu près les mêmes indices.
Par exemple, le texte formé en prenant une lettre sur 5 et en commençant à la première lettre sera exactement composé des textes prenant une lettre sur 10 et commençant respectivement à la première et à la sixième lettre.
Comme d’habitude, cela ne fonctionne bien que si l’on a un texte suffisamment long, ce qui est le cas ici.
Bon, maintenant que l’on a fait le plus difficile, il faut finir le boulot et retrouver la clé. On effectue 5 transpositions en devinant le décalage le plus probable comme pour un code de César. Ce n’est pas bien compliqué, et on obtient le texte clair.
Le premier texte extrait :
1 2 3 4 | HLLKUHULSLPHLAJJUHYLALLHJKLYBLZANTPLHABKPCYVKYBAHUVHLJKYPLVLZKJUJPXSAYZZPOVWVYEPV NYLAYWZKTHAUSVWKZLBPPLLHZAVPLPULJYLWSZTJKSLKUHUZUPHZYYLAYYASPUUKCHLHZIUXPJVLABLWW ZHZLWSYLSBULLAZUKPZAXAALLTVUTXYZNTLJJALTZUYPLSUHKYLBKULAPVVSLZLPXYUHJBVHXPBLLPNLH KLHWXAZZLLKRHOYVOLCLB |
Devient le texte suivant en utilisant le méthode pour le déchiffrement de César :
1 2 3 4 | AEEDNANELEIAETCCNARETEEACDERUESTGMIEATUDIVRODRUTANOAECDRIEOESDCNCIQLTRSSIHOPORXIO GRETRPSDMATNLOPDSEUIIEEASTOIEINECREPLSMCDLEDNANSNIASRRETRRTLINNDVAEASBNQICOETUEPP SASEPLRELUNEETSNDISTQTTEEMONMQRSGMECCTEMSNRIELNADREUDNETIOOLESEIQRNACUOAQIUEEIGEA DEAPQTS |
On procède de même pour les autres textes extraits, et on obtient le résultat !
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | ACETTEHEUREOUJEDESCENDAISAPPRENDRELEMENULEDINERETAITDEJACOMMENCEETFRANCOISECOMMAN DANTAUXFORCESDELANATUREDEVENUESSESAIDESCOMMEDANSLESFEERIESOULESGEANTSSEFONTENGAGE RCOMMECUISINIERSFRAPPAITLAHOUILLEDONNAITALAVAPEURDESPOMMESDETERREAETUVERETFAISAIT FINIRAPOINTPARLEFEULESCHEFSDOEUVRECULINAIRESDABORDPREPARESDANSDESRECIPIENTSDECERA MISTESQUIALLAIENTDESGRANDESCUVESMARMITESCHAUDRONSETPOISSONNIERESAUXTERRINESPOURLE GIBIERMOULESAPATISSERIEETPETITSPOTSDECREMEENPASSANTPARUNECOLLECTIONCOMPLETEDECASS EROLEDETOUTESDIMENSIONSJEMARRETAISAVOIRSURLATABLEOULAFILLEDECUISINEVENAITDELESECO SSERLESPETITSPOISALIGNESETNOMBRESCOMMEDESBILLESVERTESDANSUNJEUMAISMONRAVISSEMENTE TAITDEVANTLESASPERGESTREMPEESDOUTREMERETDEROSEETDONTLEPIFINEMENTPIGNOCHEDEMAUVEET DAZURSEDEGRADEINSENSIBLEMENTJUSQUAUPIEDENCORESOUILLEPOURTANTDUSOLDELEURPLANTPARDE SIRISATIONSQUINESONTPASDELATERREILMESEMBLAITQUECESNUANCESCELESTESTRAHISSAIENTLESD ELICIEUSESCREATURESQUISETAIENTAMUSEESASEMETAMORPHOSERENLEGUMESETQUIATRAVERSLEDEGU ISEMENTDELEURCHAIRCOMESTIBLEETFERMELAISSAIENTAPERCEVOIRENCESCOULEURSNAISSANTESDAU ROREENCESEBAUCHESDARCENCIELENCETTEEXTINCTIONDESOIRSBLEUSCETTEESSENCEPRECIEUSEQUEJ ERECONNAISSAISENCOREQUANDTOUTELANUITQUISUIVAITUNDINEROUJENAVAISMANGEELLESJOUAIENT DANSLEURSFARCESPOETIQUESETGROSSIERESCOMMEUNEFEERIEDESHAKESPEAREACHANGERMONPOTDECH AMBREENUNVASEDEPARFUM |
Avec la clé « HARLE1 » pour le chiffrer.
-
Personnage de Chrono cross.
 ↩
↩
Vous savez maintenant comment casser les plus anciens codes secrets, qui ont résisté plusieurs siècles pour certains ! Un petit topic propose un résumé et quelques implémentations python des méthodes étudiées. Bien entendu, les systèmes actuels de chiffrement ne sont pas aussi faibles, et heureusement.
Cependant, les méthodes sont intéressantes à connaître, car elles ont été utilisées même très récemment (Turing a fait une recherche exhaustive (très) améliorée pour casser Enigma).
J’espère que ce tuto vous aura plu ! Merci pour votre lecture  .
.




