Dans cette deuxième partie, nous allons résoudre toutes les équations du second degrés possibles. Pour cela nous allons faire une manipulation qui consiste à mettre une équation du second degré sous sa forme canonique.
Forme canonique et résolution
Équation du second degré
Une équation du second degré, c’est une équation de la forme :
où $a,b,c$ sont trois réels et avec $a\neq 0$. (Si $a$ était nul, alors ce serait l’équation d’une droite.)
Pour résoudre cette équation, il y a une méthode automatique. J’aimerais ici expliquer comment on peut trouver cette méthode en réutilisant le problème géométrique précédent.
Forme canonique
Lors de la partie précédente, nous avons étudié un cas très spécial d’équations du second degré. C’était le cas où :
c’est-à-dire où l’on avait $a=1, b=0$ et $c=y^2-r^2$. Nous avions compris cette équation comme étant l’intersection d’un cercle avec une droite horizontale. Notons par ailleurs, que l’on peut réécrire cette équation sous la forme plus simple :
L’idée de la forme canonique, c’est de ramener toute équation du second degré sous une telle forme. De sorte, que toute équation du second degré exprime en fait l’intersection d’un cercle avec une droite.
Tout d’abord, remarquons que si $a$ est non nul, alors $1/a$ est non nul, et donc
est une équation équivalente à :
qui se développe en :
Maintenant, en se remémorant l’identité remarquable :
on transforme $x^2 + \frac ba x$ en :
On obtient finalement l’équation suivante :
C’est cette équation que l’on appelle forme canonique.
En procédant au changement de variable $X = x + \frac b{2a}$ on obtient :
Retour à la géométrie
Comme vous pouvez le constater, cette dernière équation correspond à une équation de la forme
tout comme dans le cas d’un cercle et d’une droite horizontale.
Pour rappel, lors de la partie précédente, nous avions trouvé comme équation du second degré :
où $r$ était le rayon du cercle et $k$ le réel tel que $y=k$ était la droite considérée.
Maintenant, si on écrit $C$ comme différence de deux carrés : $C = c_1^2 - c_2^2$, alors on peut interpréter géométriquement l’équation $X^2+C=0$ comme l’intersection du cercle d’équation $X^2+y^2=c_2^2$ avec la droite d’équation $y=c_1^2$.
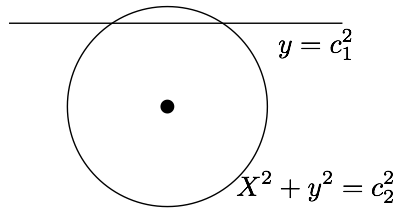
Ainsi, toutes nos équations du second degré sont bien interprétables comme étant les équations obtenues lors de la traduction algébrique du problème géométrique posé dans la première partie.
Résolution
Revenons à notre équation sous forme canonique :
et passons le dernier terme à droite :
Il nous reste alors à étudier le signe de cette dernière quantité pour obtenir le nombre de solutions et leurs valeurs (s’il y en a).
Pour étudier le signe de cette quantité, remarquons que comme $4a^2$ est strictement positif (puisque $a$ est non nul), alors :
a le même signe que $\frac{b^2}{4a^2}-\frac ca$. Cette quantité, on l’appelle le discriminant (puisqu’il discrimine les équations selon le nombre de solutions) et on le note souvent $\Delta$ :
- Si $\Delta <0$ alors il n’y a pas de solution.
- Si $\Delta = 0$ alors il y a exactement une solution.
- Si $\Delta >0$ alors il y a exactement deux solutions.
Supposons que nous sommes dans l’un des deux derniers cas. De sorte que l’on peut considérer $\sqrt \Delta$.
Notre équation :
se résout donc directement :
en sachant que si $\Delta$ est nul, alors ces deux quantités sont en fait égales (puisque $\sqrt 0 = 0$). Maintenant en se rappelant de la définition de $X$ : $X = x + \frac b{2a}$, on obtient :
On a donc résolu toute équation du second degré par une méthode générale (celle du discriminant). Et on a pu interpréter cette méthode par un problème géométrique.