Dans cette première partie, on va commencer par introduire un problème géométrique : comment décrire l’intersection d’une droite avec un cercle ? Pour cela nous allons procéder à l’algébrisation du problème, c’est-à-dire sa mise en équation, et nous verrons que la résolution de l’équation obtenue nous donne la réponse au problème géométrique posé.
Introduction : un cercle et une droite
Dessinez sur une feuille un cercle et une droite. La disposition des deux vous est totalement libre. Cependant, quoi que vous fassiez vous arriverez dans l’une des trois situations suivantes :
- ou bien la droite n’intersecte pas le cercle ;
- ou bien la droite intersecte le cercle en un point ;
- ou bien la droite intersecte le cercle en deux points.
On peut illustrer ces trois cas de figures par les dessins suivants.
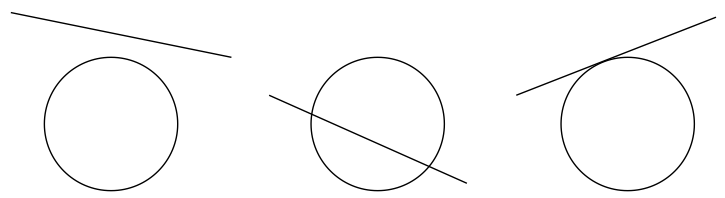
Plusieurs questions apparaissent naturellement :
- Pourquoi ne peut-on pas obtenir plus de deux points d’intersection ? (Par exemple trois points ?)
- Peut-on prédire la position des points d’intersection étant données les équations du cercle et de la droite ?
En fait nous allons répondre à la première question en répondant à la seconde. Mais cette dernière est encore trop délicate à étudier, alors nous allons faire une manipulation géométrique pour pouvoir y répondre pleinement.
L’idée, c’est d’utiliser le fait qu’un cercle est invariant par rotations. Cela signifie que l’on peut faire tourner notre figure géométrique de sorte à ce que la droite soit horizontale. Cela ne change rien à la géométrie du problème (on a simplement tourné la feuille !).
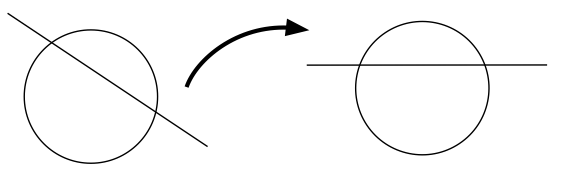
Ainsi, on se ramène à un problème plus simple qui est le suivant. Étant donnés un cercle et une droite horizontale, comment calculer les points d’intersection ?
Une fois ce problème résolu, pour revenir au cas général où la droite n’est pas nécessairement horizontale, on pourrait appliquer aux solutions la rotation inverse de celle utilisée pour se ramener au cas de la droite horizontale. Mais cette manipulation n’est pas tout à fait évidente et ne sera pas nécessaire pour traiter notre sujet : les équations du second degré. Ce retour au cas général est donc laissé en question ouverte pour ceux intéressés par la géométrie du cercle.
Équation d'un cercle et résolution
Introduction
Dans ce qui suit, nous allons établir les équations d’un cercle et d’une droite horizontale. Une fois fait nous pourrons résoudre le problème devenu alors algébrique.
On commence par choisir un repère orthonormée, de sorte que si on parle de $x$ alors on désigne une quantité réelle sur l’axe des abscisses, et que si on parle de $y$ alors on désigne une quantité réelle sur l’axe des ordonnées. De sorte que l’on peut parler du point $(x,y)$.
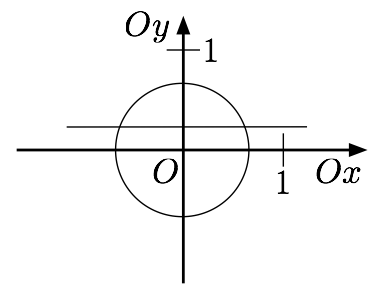
Équation d’un cercle
Qu’est-ce qu’un cercle ? Un cercle, c’est l’ensemble des points à une même distance, appelée rayon, d’un point du plan, appelé centre. Ainsi, un cercle est donné par deux objets : un rayon et un centre.
Il est usuel de choisir $(0,0)$ comme centre du cercle. Si ce n’est pas le cas pour votre repère, il faut alors introduire un nouveau repère défini par $x' = x-x_0$ et $y'=y-y_0$ où $(x_0,y_0)$ sont les coordonnées du centre de votre cercle. Cela correspond à une simple translation.
Le rayon, nous allons l’appeler $r$.
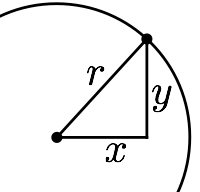
D’après le théorème de Pythagore, si $(x,y)$ est un point du cercle, alors :
Nous avons donc un candidat à l’équation d’un cercle. Cela pourrait être $x^2+y^2=r^2$ puisque tous les points du cercles vérifient cette équation. Il reste à vérifier que si un point vérifie cette équation, alors il appartient au cercle.
Mais si un point du plan $(x,y)$ vérifie $x^2+y^2=r^2$, alors d’après le théorème de Pythagore, cela signifie qu’il est à distance $r$ de l’origine, et donc appartient bien au cercle.
Ainsi, l’équation d’un cercle que l’on utilisera sera :
Il y a une équation à peine plus générale correspondant au cas où le centre du cercle serait $(x_0,y_0)$ et non plus nécessairement $(0,0)$. Cette équation se trouve de la même manière que celle donnée. Vous pouvez trouver par vous même que c’est $(x-x_0)^2 + (y-y_0)^2 = r^2$.
Équation d’une droite horizontale
Revenons maintenant à notre droite. Puisqu’elle est horizontale, cela signifie qu’un point de cette droite a sa coordonnée $y$ identique à celle des autres points de la droite. En d’autre termes, il existe un même réel $k$ tel que si $(x,y)$ est un point de la droite alors $y=k$.
Ainsi, on a un candidat à l’équation d’une telle droite :
Cette équation définit bien une droite, donc cette équation est celle recherchée.
Résolution du problème
Revenons maintenant à notre problème géométrique, qui peut maintenant être traduit algébriquement. Étant donnés un cercle et une droite donnés par les équations :
quels sont les points d’intersection ? En d’autres termes, quels sont les points $(x,y)$ vérifiant ce système ?
Tout d’abord, la seconde équation dit que si $(x,y)$ vérifie le système, alors $y=k$. On remplace donc dans la première équation la quantité $y$ par $k$. On obtient :
maintenant on fait passer le terme $k^2$ à droite :
Cette équation donne la condition nécessaire et suffisante pour qu’un point $(x,y)$ soit à l’intersection d’un cercle et d’une droite.
Mais rappelez vous que tout comme on avait trois cas possibles sur le nombre de points d’intersection (0,1 ou 2), on doit retrouver algébriquement cette distinction de cas. C’est bien ce qu’il se passe :
- Si $r^2-k^2<0$ , alors il n’existe pas de $x$ tel que $x^2 = r^2-k^2$ (puisque le carré d’un nombre réel est positif). Il n’y alors pas de point d’intersection.
- Si $r^2-k^2=0$, alors seul $x=0$ vérifie $x^2=r^2-k^2$. Ainsi, le seul point d’intersection est $(0,k)$.
- Si $r^2-k^2>0$, alors $\sqrt{r^2-k^2}$ et $-\sqrt{r^2-k^2}$ vérifient $x^2 = r^2-k^2$. Ces deux nombres sont distincts car $r^2-k^2$ n’est pas nul. Donc les deux points d’intersection sont $(\sqrt{r^2-k^2},k)$ et $(-\sqrt{r^2-k^2},k)$.
Ainsi, on a complètement résolu notre problème géométrique. On d’ailleurs montré qu’il y avait au plus deux points d’intersection car il y a au plus deux solutions à $x^2 = r^2-k^2$.
Nous avons maintenant vu comment des équations du second degré peuvent apparaître naturellement dans un problème géométrique. La partie qui suit cherchera à les résoudre dans leur plus grande généralité. Mais l’interprétation géométrique donnée dans cette partie sera réutilisable et permettra toujours de comprendre géométriquement le problème algébrique de la résolution des équations du second degré.