Dans cette partie, vous apprendrez l’essentiel sur l’objet de ce tutoriel : les signaux sinusoïdaux.
Les signaux sinusoïdaux à la loupe
Définition
Un signal sinusoïdal est un signal en forme de sinus. Formellement, il s’agit d’un signal pouvant s’écrire sous la forme suivante :
où :
- est l’amplitude du signal, positive et exprimée dans l’unité de la grandeur (des volts pour une tension par exemple) ;
- est la fréquence du signal en hertz (symbole Hz), positive comme toute fréquence ;
- est une phase à l’origine en radians (symbole rad).
La figure ci-dessous montre un exemple de signal sinusoïdal.
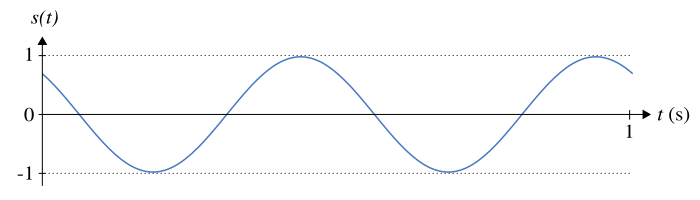
On parle d'une phase à l’origine, car il existe plusieurs valeurs qui donnent le même signal. En effet, à cause de la périodicité de la fonction cosinus, toutes les valeurs , avec entier reviennent au même. On parle souvent de la phase à l’origine, soit par abus de langage, soit pour désigner la phase à l’origine dans un domaine restreint (par exemple l’intervalle ou ).
Notez bien que la définition utilise la fonction cosinus, bien qu’on parle de signal sinusoïdal. Pour en savoir plus à propos de cette subtilité, lisez la partie Définitions alternatives.
Cas des signaux constants
Les signaux constants sont un cas particulier de signaux sinusoïdaux ! Ils sont obtenus avec une fréquence nulle, ce que nous allons démontrer.
Dans le cas d’une fréquence nulle, c’est-à-dire , l’expression d’un signal sinusoïdal devient :
Cette expression ne dépend pas du temps, il s’agit donc d’un signal constant.
Dans cette dernière expression, les deux paramètres sont redondants, puisque pour une amplitude donnée, une variation de phase à l’origine permet de retrouver toutes les amplitudes inférieures. On peut donc encore simplifier en choisissant , et obtenir le signal « sinusoïdal » constant le plus simple :
Effet des différents paramètres
Amplitude
Pour comprendre visuellement à quoi correspond l’amplitude, je vous propose de regarder les trois signaux sinusoïdaux de la figure ci-dessous.
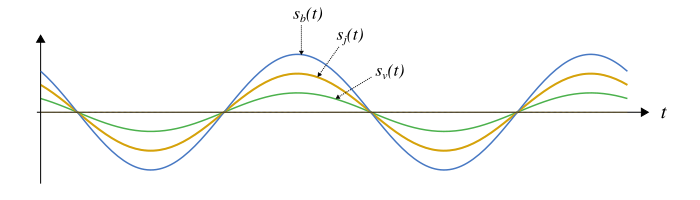
Ces signaux ont la même fréquence et la même phase à l’origine, mais diffèrent par leurs amplitudes. Il y a :
- un signal bleu, , qui oscille le plus fort,
- un signal jaune, , qui oscille moins fort,
- un signal vert, , qui oscille encore moins fort.
Les amplitudes sont telles que le signal bleu à la plus forte amplitude, suivi par le signal jaune et enfin le signal vert. On observe ainsi que plus l’amplitude est grande, plus l’oscillation est haute. Autrement dit, l’amplitude règle la hauteur des pics et la profondeur des creux.
Ce comportement se justifie mathématiquement en utilisant l’expression d’un signal sinusoïdal. Le maximum d’un signal sinusoïdal, obtenu quand le cosinus est maximal et donc égal à 1, est en effet égal à l’amplitude :
Similairement, on montre que le minimum est l’opposé de l’amplitude :
Cette observation a une conséquence pratique très utile : on peut mesurer l’amplitude d’un signal sinusoïdal, sur un oscilloscope par exemple, en mesurant le maximum ou le minimum du signal. Il est aussi possible de calculer l’amplitude en mesurant l’écart entre le maximum et le minimum, qui est le double de l’amplitude.
Fréquence
Pour comprendre visuellement à quoi correspond la fréquence, je vous propose de regarder les trois signaux sinusoïdaux ci-dessous.
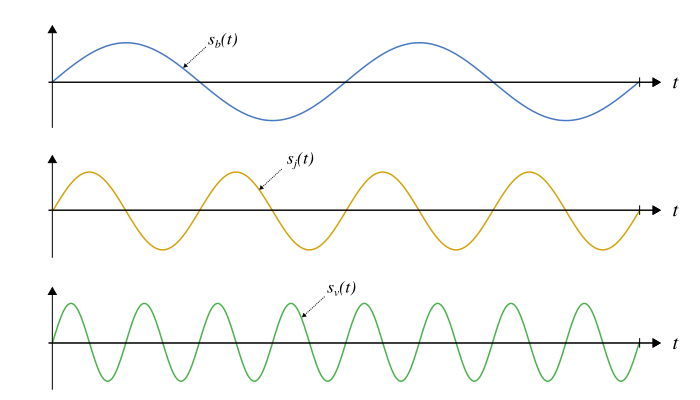
Ces signaux ne diffèrent que par leur fréquence et sont observés sur la même durée. On a :
- un signal bleu, , qui oscille le moins vite,
- un signal jaune, , qui oscille plus vite,
- un signal vert, , qui oscille encore plus vite.
Les fréquences sont telles que la fréquence du signal bleu est plus faible que celle du signal jaune, qui est elle-même plus faible que celle du signal vert. On observe ainsi que plus la fréquence est élevée, plus il y a un nombre important d’oscillations pour la même durée.
On trouve le comportement attendu pour des signaux de fréquence croissante. On peut voir cela autrement en remarquant que, à mesure que la fréquence augmente, la période diminue (pour rappel, ), ce qui peut s’observer sur la figure : le plus petit motif qui se répète devient de plus en plus étroit.
Ces observations mènent à deux méthodes pratiques pour la mesure de la fréquence. La première méthode consiste à mesurer la période, et on calcule alors la fréquence en faisant le calcul . La deuxième méthode consiste à compter le nombre (éventuellement non-entier) de répétitions du signal sur une durée donnée, et on calcule alors la fréquence en divisant le nombre de répétition par la durée.
Phase à l’origine
Pour comprendre visuellement à quoi correspond la phase à l’origine, je vous propose cette fois de regarder les trois signaux suivant.
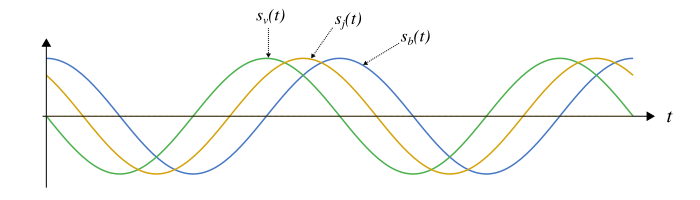
Ces signaux ne diffèrent que par leur phase à l’origine. Il y a :
- le signal bleu, , le plus à droite,
- le signal jaune, , un peu moins à droite,
- le signal vert, , encore moins à droite.
Les phases à l’origine de ces signaux sont telles que le signal bleu à une phase à l’origine plus petite que celle du signal jaune, qui lui-même à une phase à l’origine plus petite que celle du signal vert. On voit que plus la phase à l’origine est grande plus le signal se déplace vers la gauche sur la figure. En terme de temps, cela revient à dire que plus la phase à l’origine est grande, plus le signal est en avance temporelle.
Pourquoi parle-t-on de phase à l’origine ?
Pour un signal sinusoïdal, le mot phase désigne la quantité à l’intérieur du cosinus, c’est-à-dire . Le terme origine quant à lui désigne l’origine des temps, autrement dit . Si on calcule la phase pour , on obtient , la phase à l’origine. Tout est cohérent !
Animation interactive
Pour mieux appréhender ce qu’il se passe, je vous invite à jouer l’animation interactive ci-dessous. Vous pouvez voir visuellement et simplement l’effet des différents paramètres sur l’aspect du signal sinusoïdal.
Maintenant, place à quelques exercices !
Exercices
Exercice 1
Énoncé
Donner l’amplitude et la fréquence du signal sinusoïdal ci-dessous.
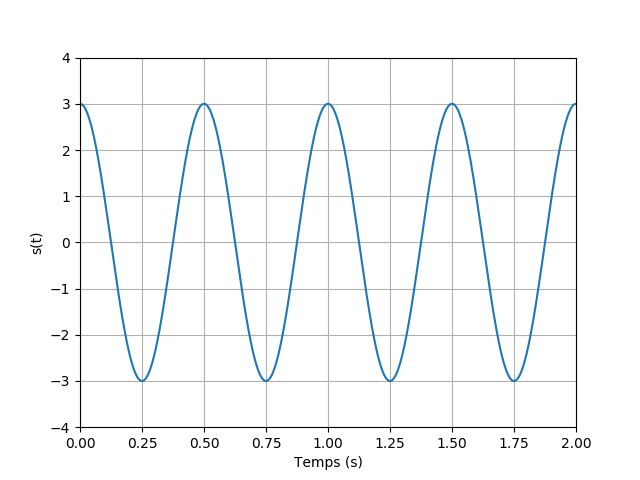
Réponse
On peut mesurer la période, par exemple à partir de l’écart entre deux maximums. On trouve :
On en déduit la fréquence :
Pour l’amplitude, il suffit de mesurer la hauteur du maximum, ce qui donne une amplitude de 3.
Exercice 2
Énoncé
Donner l’amplitude et la fréquence du signal sinusoïdal ci-dessous.
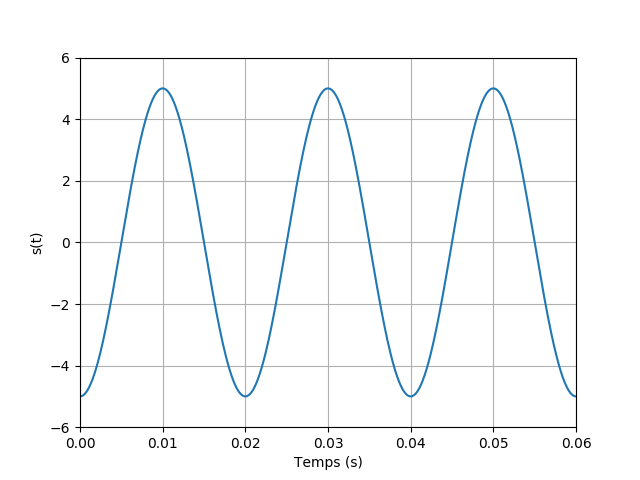
Réponse
Pour cet exercice, on peut procéder exactement comme pour le premier, ce qui nous donne une fréquence de 50 Hz et une amplitude égale à 5.
Exercice 3 (plus dur)
Énoncé
Pour chacun des deux signaux précédents, donner une phase à l’origine , sachant que les signaux sont de la forme :
Réponse
Nous n’avons pas parlé de mesure de phase à l’origine à ce stade du cours. Cependant, les deux signaux précédents sont des cas particuliers.
Dans le premier cas, à , le signal atteint son maximum. Autrement dit, le terme vaut 1. Or, le cosinus est maximal notamment pour une phase nulle. Ainsi, une phase à l’origine du premier signal est .
Dans le deuxième cas, le signal est minimal pour , ce qui signifie que le terme est égal à -1. Or, ceci est vrai notamment pour une phase égale à . Ainsi, une phase à l’origine du deuxième signal est .
Annexe : Définitions alternatives
Forme alternative avec la période
La fréquence d’un signal est liée à sa période par la relation suivante :
Ainsi, vous verrez parfois des signaux sinusoïdaux écrits avec la période au lieu de la fréquence :
Cette forme est évidemment équivalente à la forme habituelle.
Forme alternative avec la pulsation
La pulsation est liée à la fréquence par la définition suivante :
Ainsi, vous verrez fréquemment des signaux sinusoïdaux écrits avec la pulsation au lieu de la fréquence :
Cette forme est souvent appréciée pour sa compacité. On laisse en effet de côté le facteur qui prend systématiquement de la place sans apporter beaucoup d’information.
Forme alternative avec un sinus
Définition
Il existe une définition alternative pour les signaux sinusoïdaux qui utilise la fonction sinus :
Elle ressemble évidemment à la définition avec le cosinus, et elle y est même équivalente. On peut en effet simplement passer de la définition avec le cosinus à celle avec le sinus en ajoutant à la phase à l’origine.
Passage de la définition en cosinus à celle en sinus
Il est possible de démontrer ce changement de variable grâce à quelques calculs trigonométriques.
On part de la définition d’un signal sinusoïdal à l’aide de la fonction cosinus :
Cette définition peut être transformée à l’aide de l’identité trigonométrique suivante :
En transformant la définition, on obtient une forme avec un sinus :
En posant , on obtient finalement :
Voilà, on a montré qu’il suffit d’ajouter à la phase à l’origine !
Plus généralement, il est possible d’ajouter n’importe quel nombre de la forme , avec entier, pour obtenir le même effet.
Pourquoi avoir choisi la définition avec les cosinus pour ce cours ?
Dans ce cours, nous avons fait le choix d’énoncer la définition de signal sinusoïdal en utilisant la fonction cosinus. Pourtant, nous venons de voir qu’il est possible de manière équivalente de l’énoncer avec des sinus.
Ce qui fait pencher la balance, c’est l’écriture trigonométrique des nombres complexes. En effet, un nombre complexe de module et d’argument peut s’écrire sous la forme suivante :
Dans ce cas, la partie réelle est exprimée avec un cosinus :
En prenant et , on peut dire que est alors un signal complexe, dont la partie réelle est le vrai signal sinusoïdal.
Cette observation est à la base de la notation complexe des signaux sinusoïdaux, qui mérite tout un tutoriel à elle seule. Elle est très utilisée en électronique, car elle permet une grande simplification des calculs.
Maintenant que vous savez l’essentiel sur le signaux sinusoïdaux, le moment est venu de voir comment on peut les comparer.