Collisions spécifiques

Notre premier exemple : Pong, un des plus vieux jeu vidéo.

Présentation

On ne présente plus Pong : 2 raquettes, et une balle. La balle rebondit sur les murs, et si on ne la rattrape pas, on perd le point.

L’algorithme de collisions testera donc la collision avec chacune des raquettes. La balle est carrée, les raquettes sont rectangles, comme dans le Pong original. Notez que si la balle est ronde, on peut considérer sa zone de collision comme un carré.

Première idée

Notre première approche sera donc de détecter les collisions AABB, vues au début de ce chapitre, entre la balle et chacune des raquettes.

Cela serait rapide avec nos machines actuelles. A chaque itération de notre boucle principale, 2 tests de collision à faire. Le if qu’il y a dans la fonction de collision effectue cependant plusieurs tests, même s’ils sont rapides.

Nous pouvons aller encore plus vite, et faire moins de calcul, ce qui n’était pas du luxe pour les premières machines qui ont fait tourner Pong.

Test spécifique

Regardons l’image ci dessus. J’ai rajouté 2 traits verticaux rouges. L’idée est simple, si la balle traverse un de ces traits rouge, alors on doit tester si on touche la raquette concernée ou non. Soit la balle rebondit, soit on perd un point.

Dans Pong, les raquettes se déplacent verticalement, mais pas latéralement. De ce fait, la position de ces hypothétiques traits rouges sera constante.

Si on regarde à gauche, le trait rouge touche la raquette, si on regarde à droite, ce n’est pas le cas, pourquoi ? Eh bien parce que la position de la balle est définie par son coin supérieur gauche. De ce fait, si le coin supérieur gauche touche le trait rouge de droite, alors la balle touche la raquette, l’espace entre le trait et la raquette étant la largeur de la balle. Cela nous évitera de calculer sans cesse le point de droite de la balle.

De ce fait, dans notre boucle principale, au lieu d’appeler 2 fois une fonction de collision à plusieurs tests, nous allons faire uniquement 2 tests.

if (balle.x < X_TRAIT_ROUGE_GAUCHE)
{
    TestCollisionY(balle, raquette1);
    ...
}
if (balle.x > X_TRAIT_ROUGE_DROITE)
{
    TestCollisionY(balle, raquette2);
    ...
}

Dans la majorité des cas, quand la balle transite au milieu, on ne rentrera pas dans ces if. Que faire maintenant si on rentre dans le if ? Il suffira de tester la position y de la balle, par rapport à celle de la raquette.

La balle touchera la raquette si :

• balle.y + balle.h > raquette.y
• balle.y < raquette.y + raquette.w

Sinon, elle ne touche pas, et on perd le point.

Cela peut s’écrire aussi :

• balle.y > raquette.y - balle.h
• balle.y < raquette.y + raquette.w

Si on regarde de nouveau le dessin ci-dessus, on voit le trait jaune qui correspond à la position raquette.y - balle.h.

Cet algorithme sera un petit peu plus rapide que les collisions AABB, et il est plus intuitif, même si sur nos machines actuelles, cela n’a plus aucune importance pour un Pong.

Voici maintenant une astuce pour les collisions dans un jeu de course vu du dessus sur des pistes courbes. C’est ce topic qui m’a inspiré cette idée.

Présentation

Vous avez dessiné une piste comme ci-dessous :

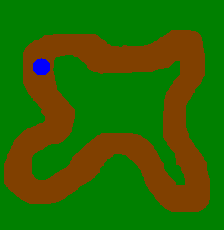
Votre route est la zone marron. Vous êtes le véhicule bleu, et vous souhaitez tester les collisions avec le décor (le vert). L’idée étant de ne pas sortir. Vous déplacez votre véhicule et vous voulez tester la collision avec le décor.

Pourquoi un cercle ?

Dans ce genre de jeux, la voiture peut tourner à 360°. Nous pouvons donc considérer une OBB qui s’adaptera à l’angle de rotation de la voiture, ou bien considérer que la voiture n’est pas trop longue, et donc s’inscrira dans un cercle qui lui ne dépendra donc pas de l’angle de rotation, ce sera plus simple, et tout aussi efficace.

Voici une image du jeu "micro machine" qui gère probablement ses collisions avec des cercles. J’ai rajouté les cercles moi même sur l’image, en mauve :

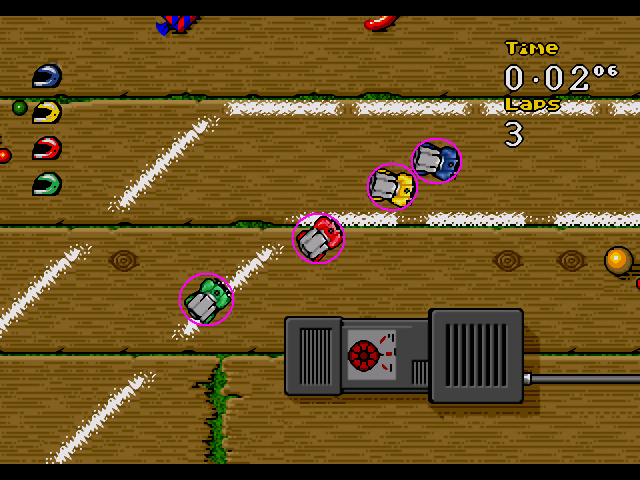
Première idée

Si on considère le problème de cette manière, la première idée est de tester la collision d’un cercle avec des pixels verts. En effet, si un seul pixel bleu touche le vert, alors il y a collision. Nous pensons donc à ce lourd algorithme qu’est le pixel perfect, décrit plus haut dans ce tutoriel.

L’idée sera donc de tester chaque point du cercle, et voir s’il touche le bord. C’est assez long et lourd.

Les propriétés du cercle

Nous avons donc dit que nous allions nous servir du cercle pour les collisions. Mais au lieu de tester chaque point du cercle, nous allons nous appuyer sur une propriété du cercle :

Donc l’idée est simple, au lieu de considérer tout le cercle et chacun de ses points, on ne considère que le centre du cercle, et on regarde si sa distance au bord de la route est inférieure ou supérieure au rayon. Pour cela, nous allons dessiner sur la carte les zones ou la distance au bord est plus petite que le rayon. Cela, on peut le définir graphiquement, regardez :

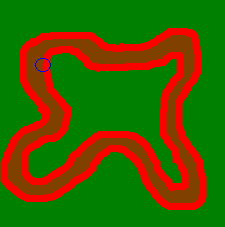
Ici, j’ai redessiné la même route, mais, j’ai dessiné au bord une bande rouge qui a pour largeur le rayon du cercle. J’ai redessiné le cercle bleu. Le cercle touche la bordure verte. On constate que son centre, lui, touche la bordure rouge. On peut donc dire :

L’idée sera donc de dessiner cette bande rouge sur le schéma de vos circuits. Évidemment, vous ne serez pas obligés de l’afficher. Nous utiliserons donc le concept plus rapide des masques décrite dans le chapitre précédent, vous pourrez avoir deux images : une pour le circuit, une pour le masque.

Collision

Pour savoir si votre voiture touche le bord, il suffira donc de tester si le pixel centre du cercle touche, dans le masque, un pixel rouge (ou vert), ou pas. Un seul pixel à tester !

Dessiner la bande rouge

Pour avoir de belles collisions, il faudra que la bande rouge ait bien la largueur correspondante au rayon du cercle. Pour cela, les logiciels de dessins proposent un pinceau dont on peut souvent définir la largueur. Cela rend de bons résultats, suffisants.

Approche mathématique

Pour la plupart d’entre vous, cette partie ne servira pas. Un coup de pinceau de bonne largeur dans Paint suffit à donner un bon résultat. Cette partie sert juste à définir mathématiquement le concept évoqué.

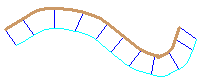
Si on considère que le bord de la route est une courbe $C$, alors le bord de la zone rouge est la courbe offset O de la courbe $C$, à distance $d$. Une courbe d’offset, c’est une courbe dont chaque point est à une distance d fixée de la courbe originale.

Ci dessus, si on regarde la courbe bleu ciel, elle est en tout point à égale distance de la courbe marron. Chaque segment bleu fait la même longueur.

La courbe offset $O(u)$, à distance $d$, de la courbe $C(u)$ se définit par la formule suivante :

$N(u)$ est la normale à la courbe au point de paramètre $u$.

$N(u)=\dfrac{C′(u)∧A}{||C′(u)∧A||}$ avec A vecteur normal au plan $A=(0,0,1)$

Voici maintenant des petits algorithmes de collision pour les labyrinthes.

Définition

Nous allons parler des labyrinthes basés sur une grille, comme ci-dessous :

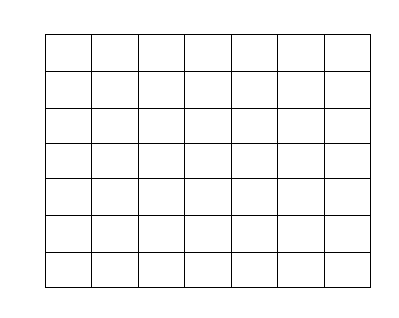
Il existe plusieurs types de codage pour les labyrinthes. En voici deux formes :

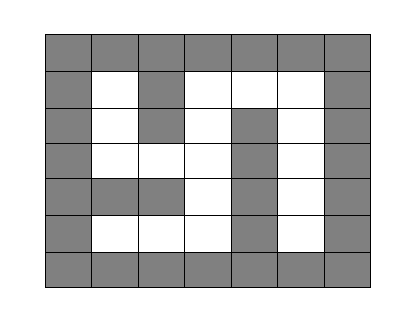
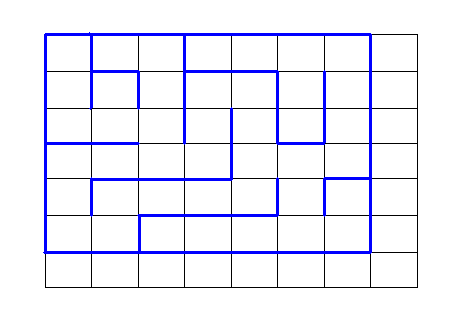
La première forme, nous l’avons déjà rencontrée quand nous parlions du tile mapping dans ce tutoriel. La collision est donc du même type, à savoir déterminer au dessus de quelle(s) case(s) est notre personnage, puis dire qu’il y a collision si une de ces cases est un mur.

Nous allons nous intéresser au deuxième cas, où cette fois les murs sont fins, et sont les bords de chaque carré de la grille.

Codage

Avant de parler collision, il faut voir comment ceci est codé en mémoire. Ici, nous considèrerons un codage basé sur une grille comme le tile mapping.

Nous aurons donc le labyrinthe stocké en tant que tableau en deux dimensions de "Case". Chaque case aura chacun de ses bords qui sera un mur ou non. La première idée est donc de se dire "chaque case a donc 4 murs potentiels", un en haut, un en bas, un à gauche, un à droite. Mais si vous regardez mieux, vous verrez qu’on peut même considérer chaque case comme ayant potentiellement 2 murs : un en haut, un à gauche.

Regardez cette image :

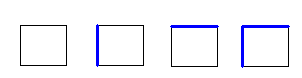
Voici les 4 types de cases nécessaires et suffisants pour reconstruire le labyrinthe ci-dessus. Regardez l’image ci-dessus et constatez que l’on peut construire ce résultat avec seulement ces 4 cases là.

C’est économique, et il n’y a pas de redondances, contrairement à un codage avec 4 murs par case.

Le seul inconvénient, qui n’en est pas vraiment un, est qu’on n’ira jamais sur les cases tout à droite et tout en bas du labyrinthe : l’image ci-dessus le montre, on a l’impression que la ligne du bas, et la colonne de droite sont de trop, alors qu’elles permettent simplement de ne pas faire d’exceptions pour notre codage.

Bref, un labyrinthe est donc un tableau en 2D de cases qui contiennent chacune uniquement 2 bits : une pour le mur d’en haut (présent ou non), un pour le mur de gauche.

Si on illustre cela par du pseudo code, on obtient :

struct Case
{
    unsigned int murgauche: 1;  // variable d'un bit
    unsigned int murhaut: 1;  // variable d'un bit
};

struct Laby
{
    struct Case** Tableau;   // tableau 2D. Certains préfèreront la syntaxe : Case[X][Y];
    int X, Y;  // taille labyrinthe
    int LARGEURCASE, HAUTEURCASE; // nom explicite
    int Orx, Ory;  // Origine du labyrinthe en x et y : si la première case ne commence pas à (0,0)
};

Calcul de collision

À partir de là, voici comment on va faire pour savoir si on touche un mur. Observons ci-dessous une image qui nous servira d’exemple :

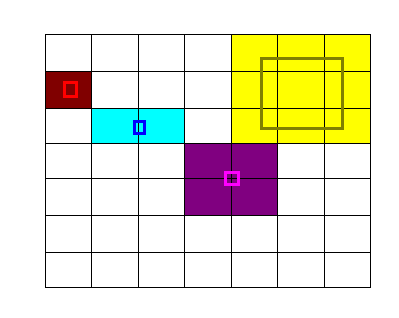
Les carrés de couleur creux représentent les AABB de notre personnage, et les zones de couleurs derrière représentent les cases de la grille impliquées.

Le calcul de zones de couleur derrière se fait de la même manière que dans le cas des tiles vu plus haut. Rappelez-vous, la zone sera rectangulaire, les coordonnées minimales seront les coordonnées de la zone que touche le point en haut à gauche, et les coordonnées maximales seront les coordonnées de la zone que touche le point en bas à droite.

Tout s’appuie donc sur une fonction GetPointPosition, qui va, pour un pixel $x,y$ donné, dire dans quelle case $(xc,yc)$ il est :

void GetPointPosition(Laby L, int x, int y, int * xc, int * yc)
{
    *xc = (x - L.Orx) / L.LARGEURCASE;
    *yc = (x - L.Ory) / L.HAUTEURCASE;
}

Notez que si votre grille commence à la coordonnée $(0,0)$, alors on retombe sur une simple division.

Le début de la fonction collision consiste donc à calculer xmin, ymin, xmax, ymax, coordonnées minimales et maximales des cases à analyser en fonction de la AABB de notre personnage à tester.

int Collision(Laby L, AABB box)
{
    int xmin, xmax, ymin, ymax;
    GetPointPosition(L, box.x, box.y, &xmin, &ymin);
    GetPointPosition(L, box.x + box.w - 1, box.y + box.h - 1, &xmin, &ymin);
   ...
}

Une fois que nous avons xmin,xmax,ymin,ymax, il ne reste plus qu’à tester s’il y a un mur au milieu de la zone.

• Si on regarde la zone rouge ci-dessus : le personnage est inclus dans une seule case. On a xmin = xmax et ymin = ymax : pas de collision avec le mur possible.
• Si on regarde la zone bleue : il y aura collision uniquement si la case de droite a son mur gauche actif (concrètement, le mur vertical entre les deux).
• Si on regarde la zone violette, il faudra vérifier tous les murs (traits noirs) au milieu, et pareil pour la zone jaune, où l’on considère un gros personnage !

Si un seul de ces murs est présent, alors notre personnage touche un mur, et il y a collision. Le code suivant illustre simplement cela :

int Collision(Laby L, AABB box)
{
    int xmin, xmax, ymin, ymax;
    GetPointPosition(L, box.x, box.y, &xmin, &ymin);
    GetPointPosition(L, box.x + box.w - 1, box.y + box.h - 1, &xmin, &ymin);
    for(i = xmin; i <= xmax; i++)
    {
        for(j = ymin; j <= ymax; j++)
        {
            if (i != xmin && L.Tableau[i][j].murgauche == 1)
                return 1;
            if (j != ymin && L.Tableau[i][j].murhaut == 1)
                return 1;
        }
    }
    return 0; // pas de collision.
}