Jusqu’à présent, nous avons vu les collisions entre objets potentiellement mobiles. Nous allons ici voir les différentes collisions avec des décors fixes.
Sol
Nous allons voir maintenant comment tester la collision avec le sol. Tout d’abord avec un sol plat, puis un sol bien courbe.
Applications


Nous voyons en haut Street Fighter 2 où le sol est plat. Si le personnage saute et retombe sur le sol, il faut qu’il s’arrête. En bas, Rayman évolue dans un monde ou le sol est en pente. En réalité, je pense que Rayman utilise un système de tiles amélioré, mais imaginons que non.
Calcul de collision
Sol plat
Le sol plat n’a qu’un seul paramètre : son altitude a. Nous souhaitons savoir si la bounding box de notre personnage passe à travers ou pas. La signature de notre fonction sera la suivante.
bool Collision(AABB box, int a)
Pour savoir si on passe à travers, c’est très simple : si l’ordonnée du point du bas de la bounding box est supérieure à a, alors on passe à travers, sinon, non. La fonction est donc triviale.
bool Collision(AABB box,int a)
{
if (box.y + box.h >=a)
return true;
else
return false;
}
Sol courbe
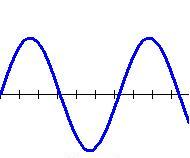
Voici une belle fonction sinus (à gauche). Pensez vous qu’on puisse marcher dessus ? En réalité, c’est très facile… Notre fonction aura cette signature.
bool Collision(AABB box,fonction f)
f est un pointeur de fonction (c’est pour illustrer le principe, vous pouvez faire sans).
Pour savoir si le perso touche ou pas la fonction, nous n’allons considérer qu’un seul point x,y : celui en bas au milieu de la AABB (point mauve sur l’image de droite ci-desssous). Comment savoir si le joueur est en dessus ou en dessous de la courbe ? Il suffit de voir si f(x) > y ou non.

Cela donne la chose suivante :
bool Collision(AABB box,fonction f)
{
int x = box.x + box.w/2; // point milieu bas.
int y = box.y + box.h;
if (f(x)>y)
return true;
else
return false;
}
Toute la difficulté revient à avoir l’équation du sol. Il faut pouvoir dire, pour un x donné, où est la coordonnée y du sol, un f(x) = y. Souvent, on voudra une courbe qui passe par des points qu’on aura choisis. Les splines cubiques sont de bonnes candidates. Mais cela sort du cadre de ce tuto.
Ce chapitre vous montre déjà comment marcher sur une fonction mathématique… Vous penserez à un petit bonhomme qui se déplace sur la fonction que votre prof de maths dessinera au tableau ! 
J’ai même une astuce supplémentaire pour vous faire utiliser les dérivées. Dans certains jeux où il y a des pentes, le personnage peut gravir la pente si elle est douce, et glisse si elle est « trop raide ». Comment savoir cela ? Il suffit de calculer la dérivée , et de voir sa valeur absolue. Si elle est plus grande qu’un seuil que vous fixerez, vous pourrez dire que c’est trop pentu et jouer en conséquence…
Le calcul de dérivée, vous n’avez pas à le programmer, vous le pré-calculez sur une feuille. Par exemple, si vous marchez sur la fonction , vous savez que sa dérivée est . Pour les splines cubiques, ce sont des polynômes. Un polynôme se dérive facilement…
Cette technique de collision n’est pas très utilisée dans les jeux 2D (à ma connaissance), les jeux de plateforme avec pentes préféreront un concept de tiles améliorés, dont nous parlerons plus bas. Cependant, beaucoup de jeux 3D utilisent ce concept, dans ce qu’on appellera la Heightmap. Nous verrons ça par la suite.
Tiles droits
Dans beaucoup de jeux 2D, les décors sont définis par des tiles. Si vous voulez approfondir ce concept, je vous invite à lire mon tutoriel sur le TileMapping.
Définition
Les jeux exploitant le tilemapping sont reconnaissables par leurs carreaux répétitifs régulièrement placées. Si on regarde l’image ci dessous :
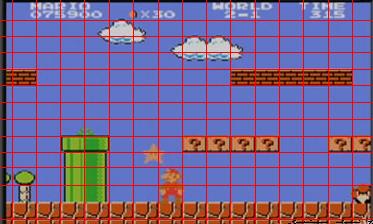
Nous pouvons constater que les blocs se répètent et s’inscrivent exactement dans une grille de taille régulière. Stocker le TileMapping en mémoire revient juste à stocker les dessins de quelques blocs, et un tableau de nombres (appelés indices), qui permettent de construire l’image, comme le montre ce schéma.
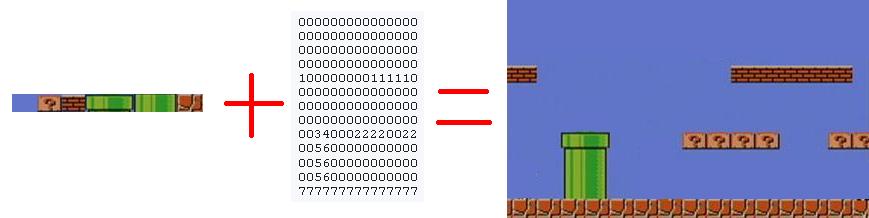
A gauche, j’ai 8 petits dessins (numérotés de 0 a 7). Au milieu, j’ai un tableau de nombres. A partir de la, je peux reconstruire l’image de droite. Pour afficher l’image, il suffira d’appliquer l’algorithme formel suivant.
// soit T le tableau de nombres, de dimension X,Y
for(i=0;i<X;i++)
{
for(j=0;j<X;j++)
{
typetile = T[i][j];
px = i*LARGEUR_TILE;
py = i*HAUTEUR_TILE;
BlitTile(typetile,px,py); // blit le tile typetile a la position px,py
}
}
La grille étant régulière, LARGEUR_TILE et HAUTEUR_TILE sont constants. Sur le dessin ci dessus, c’est l’écart qu’il y a entre 2 lignes verticales (pour la largeur) et 2 lignes verticales (pour la hauteur).
Même si parfois, en mémoire, c’est légèrement plus complexe, il y a toujours cette notion de tableau à 2 dimensions qui réfèrent un type de tile. Certains tiles seront des murs, d’autres non.
Pour ce tuto, je définirai la fonction suivante qui me dira si le tile à la position i,j est un mur ou non.
bool TileIsMur(int i,int j);
Applications
Les jeux utilisant le tilemapping sont légion.



Zelda, Mario, les jeux de plateforme des consoles 8 bits et 16 bits utilisent du tilemapping. Même si, dans le 3e exemple (Secret of mana), ce n’est pas flagrant, ce sont des tiles.
Calcul de collision
Juste un point dans le mur
Comment savoir si un point donné touche un mur ou non ? Cela est extrêmement simple. Vous avez un point à tester. Il suffit de savoir au dessus de quelle case de la grille il est. On regardera ensuite si le tile correspondant à cette case est un mur ou non…
Nous partons du principe que la grille commence à la coordonnée .
Il suffira, pour avoir les coordonnées du tile concerné, d’une simple division.
i = x / LARGEURTILE
j = y / HAUTEURTILE
Nous prendrons la partie entière de i et j. Autrement dit, si la division donne 5.1 ou 5.9, nous prendrons 5. En C, le fait de diviser deux int donne une division entière, ce qui donne notre résultat.
Il ne s’agit pas d’arrondir mais bien de prendre la partie entière. Si on arrondit 5.9, on trouve 6, si on prend sa partie entière, on a 5. Et on attend 5.
Cela nous donne immédiatement la code suivant.
bool CollisionTile(int x, int y)
{
int i = x / LARGEUR_TILE;
int j = y / HAUTEUR_TILE;
return TileIsMur(i,j);
}
Variante : si votre grille ne démarre pas à la coordonnée mais à la coordonnée , la variante est extrêmement simple.
int i = (x - a) / LARGEUR_TILE;
int j = (y - b) / HAUTEUR_TILE;
Une AABB dans le mur
Votre Mario n’est pas un point mais une AABB, et vous souhaitez savoir s’il touche un mur. Regardons le dessin ci dessous.
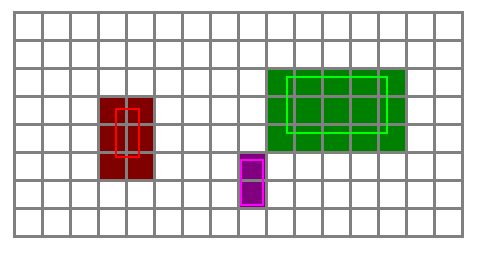
Nous voyons la grille, et quelques AABB à tester (en couleurs claires). Pour savoir si le personnage touche le mur, il suffit de tester tous les tiles que coupent la AABB.
Alors il faut déjà calculer l’intersection entre tous les tiles possibles et notre AABB, ce sera long !
Et bien non, puisque comme la grille est droite, et que la AABB aussi, alors il suffira de considérer comme le point supérieur gauche de la AABB et comme le coin inférieur droit. Les tiles concernés seront tous ceux dans le rectangle et . Sur le dessin, cela nous donne les tiles remplis de couleur foncées.
Si un seul de ces tiles à tester est un mur, alors notre perso est dans un mur. Si aucun n’est un mur, alors on n’est pas dans un mur.
Voici le code.
bool CollisionTiles(AABB box)
{
i1 = box.x/LARGEUR_TILE;;
j1 = box.y/HAUTEUR_TILE;
i2 = (box.x + box.w -1)/LARGEUR_TILE;
j2 = (box.y + box.h -1)/HAUTEUR_TILE;
int i,j;
for(i=i1;i<=i2;i++)
{
for(j=j1;j<=j2;j++)
{
if (TileIsMur(i,j))
return true;
}
}
return false; // si on n'est pas sorti avant, c'est qu'on ne touche aucun tile.
}
Pour des exemples appliqués et complets sur le tilemapping, je vous invite à lire mon tuto sur le Tilemapping.
Tiles isométriques
Définition
On parle de tile isométrique quand, au lieu d’être un rectangle, le tile est incliné comme ci dessous.
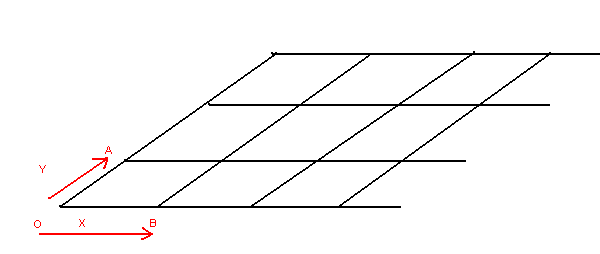
Cela permet de simuler un effet 3D, et est très utilisé dans les jeux 2D qui veulent donner une sorte de profondeur.
Applications
Les jeux suivants utilisent des tiles isométriques.

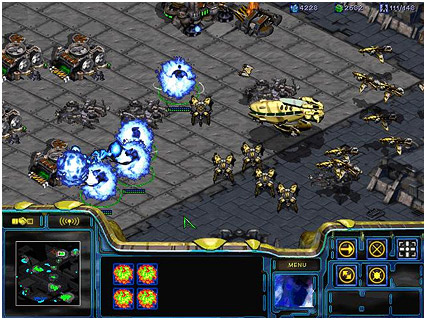
On voit bien le sol « penché », qui nous donne un effet de profondeur. De plus, pour donner une sorte d’altitude, des objets sont blittés par dessus, comme les barrières dans Diablo (image du haut) ce qui nous donne une réelle impression de 3D, alors que ce n’est que de la 2D.
Calcul de collision
Point dans un tile isométrique
Imaginons que vous ayez un point (sur l’écran), et vous avez envie de savoir sur quel tile isométrique il est (par exemple, vous voulez cliquer dessus). Revoyons notre image.

Ma grille isométrique commence au point O de coordonnée . Je définis le repère du monde de tiles par deux vecteurs X et Y, sont les vecteurs et .
Il vous suffit de trois points O,A,B pour définir votre grille. Nous définissons ainsi le repère de la grille isométrique.
Si on considère O comme le point d’ancrage du tile de coordonnée , pour avoir le point d’ancrage P du tile de coordonnée , il suffit de faire :
Si on pose Q de coordonnée , on a alors, de façon matricielle :
Avec M la matrice du repère O,X,Y :
Ce qui nous donne :
Ceci est l’écriture matricielle de . Grâce à cela, pour un donné, nous pouvons calculer le point correspondant dans le repère de l’écran.
Oui, mais nous voulons l’inverse : nous avons le point dans le repère de l’écran, et nous voulons savoir sur quel tile il est, autrement dit quelle est sa coordonnée dans le repère de la grille. Autrement dit, nous avons P, nous voulons connaître Q.
Si alors avec qui est l’inverse de la matrice .
Si vous ne connaissez pas les matrices en maths, sachez juste que c’est un outil puissant pour changer de repère. Votre écran est un repère, la grille en est un autre. Vous avez un point dans un repère, vous voulez savoir quelle est sa coordonnée dans l’autre ? Utilisez des matrices.
Voici donc les étapes que nous devons effectuer.
- Nous avons et dans l’écran.
- Nous devons calculer et .
- Nous devons calculer .
- Nous devons construire .
- Nous devons calculer .
- Nous devons multiplier cette dernière par .
- Nous récupérons , nous faisons une division entière comme pour les tiles droits ci dessus, et nous pourrons dire que le clic touche le tile .
Calculer et
Si on regarde le dessin ci dessus, c’est simple.
Ce sont des vecteurs, on pose 0 comme dernière coordonnée.
O est le point origine de la grille. On peut l’écrire ainsi :
O est un point, on pose 1 comme dernière coordonnée.
Calculer P
P, c’est point que j’ai en entrée.
P est un point, on pose 1 comme dernière coordonnée. Nous cherchons :
Q est un point, on pose 1 comme dernière coordonnée.
Calculer M
La matrice d’un repère en 2D est une matrice 3 lignes et 3 colonnes. La construire est simple, ayant la repère , la matrice est simplement .
Si on prend l’expression des points et vecteurs ci dessus, on trouve bien :
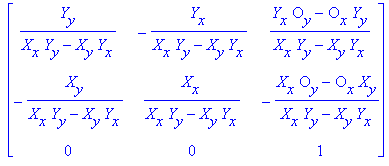
Calculer
est l’inverse de la matrice . Je vous renvoie a vos cours de maths. Nous trouvons
Multiplication par P
Enfin, pour avoir , et donc et , il faut multiplier par , ce qui nous donne :
Au niveau du code, cela nous donne :
bool CollisionIso(Point O,Point A,Point B,float x,float y)
{
Vecteur X,Y;
X.x = B.x - O.x;
X.y = B.y - O.y;
Y.x = A.x - O.x;
Y.y = A.y - O.y;
float denom = X.x*Y.y-X.y*Y.x;
// coordonnées réelles de x,y dans repère de la grille.
float fi = (Y.y*x - Y.x*y + Y.x*O.y-O.x*Y.y)/denom; // i et j non tronqués.
float fj = -(X.y*x - X.x*y + X*x*O.y-O.x*X.y)/denom;
// prendre la partie entière pour savoir sur quel tile on est.
int i = (int)fi;
int j = (int)fj; // vous pouvez modifier la fonction pour renvoyer i et j.
// est ce que ce tile est un mur ?
return TileIsMur(i,j);
}
Ce calcul marchera dans dans les cas quelconques. Dans le dessin ci dessus, l’axe X est bien horizontal, ce qui nous permettrait de simplifier quelques calculs. Mais qui peut le plus peut le moins dit on !
Rectangle dans tile iso
Je suis sûr que vous me voyez déjà venir avec de gros calculs, mais il n’en est rien ici.
L’astuce, quand on fait un jeu isométrique, c’est de garder en mémoire les mêmes données que si c’était droit. En effet, Si on regarde un jeu isométrique, on peut l’imaginer comme un jeu "droit". Tout calcul de collision entre objets marchera de la même manière.
Et c’est seulement au moment de l’affichage que vous dessinerez vos tiles en biais. Et c’est également seulement quand vous cliquez sur un tile que vous calculerez le point dans le repère de la grille comme vu au chapitre précédent. Mais en mémoire, tout se passe dans le repère de la grille. Donc toute collision entre objets, tout objet avec les murs, se passe comme dans un monde de tiles droits.
D’autres types de collisions viendront enrichir prochainement ce paragraphe.