Formes simples

Voici maintenant quelques algorithmes de collision en 3D. Pour commencer, voyons les collisions AABB mais en 3D.

Définition

Une Bounding Box 3D, alignée avec les axes, est comme une bounding box 2D vue au dessus, mais avec une dimension supplémentaire.

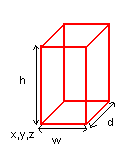
Nous pourrons définir la structure suivante :

struct AABB3D
{
    float x, y, z;
    float w, h, d; 
};

Nous avons les coordonnées $x,y,z$ du point le plus proche de l’origine du monde, et la largeur $w$ (width), la hauteur $h$ (height) et la profondeur $d$ (depth).

En 3D, il est d’usage de travailler avec des coordonnées réelles, donc des nombres flottants. Nous travaillons donc dans l’espace réel $R^3$.

Applications

Ce type de collision est très utilisé dans les jeux 3D. Ici dans Descent FreeSpace pour détecter les collisions entre vos tirs et les vaisseaux ennemis :

Calcul de collision

Point dans AABB3D

Le calcul est très similaire à celui du premier chapitre. Il suffit de vérifier si le point (de coordonnées $x,y,z$ est entre 6 parois de la AABB3D.

bool Collision(float x, float y, float z, AABB3D box)
{
   if (x >= box.x 
    && x < box.x + box.w
    && y >= box.y 
    && y < box.y + box.h
    && z >= box.z 
    && z < box.z + box.d)
       return true;
   else
       return false;
}

Collision de deux AABB3D

De même, le concept ici est vraiment très proche de celui de collision de deux AABB (2D). Il faudra vérifier, pour une box1, si la box2 n’est pas « trop à gauche », « trop à droite », « trop en haut », ou « trop en bas », comme pour les box 2D, mais également qu’elle ne soit pas non plus « trop devant » et « trop derrière ».

Il suffit d’enrichir le if de la fonction, et nous obtenons alors la fonction suivante :

bool Collision(AABB3D box1, AABB3D box2)
{
   if((box2.x >= box1.x + box1.w)      // trop à droite
    || (box2.x + box2.w <= box1.x) // trop à gauche
    || (box2.y >= box1.y + box1.h) // trop en bas
    || (box2.y + box2.h <= box1.y)  // trop en haut 
        || (box2.z >= box1.z + box1.d)   // trop derrière
    || (box2.z + box2.d <= box1.z))  // trop devant
          return false; 
   else
          return true; 
}

Les bounding sphères sont une application en 3D des algorithmes sur les cercles que nous avons vu plus haut.

Définition

Une sphère est définie par son centre $(x,y,z)$ et son rayon.

En C, on peut définir cette structure :

struct Sphere
{
  float x, y, z;
  float rayon;
};

Applications

Un jeu de billard en 3D peut utiliser ce type de collisions. Également d’autres shoot’em up 3D (tel Descent FreeSpace vu ci-dessus) si on considère les vaisseaux inscrits dans des sphères au lieu de AABB3D, les 2 formes peuvent donner de bons résultats).

Calcul de collision

Les calculs sont très similaires à ceux vus dans le chapitre sur les cercles en 2D. Ils se basent sur le calcul de distance 3D. Ce calcul est une généralisation de Pythagore dans l’espace :

Avec la même astuce, considérant la distance au carré, nous arrivons aux deux fonctions suivantes :

Point dans une sphère

Soit le point $(x,y,z)$, nous souhaitons savoir s’il est dans la sphère :

bool Collision(float x, float y, float z, Sphere S)
{
   int d2 = (x - S.x) * (x - S.x) + (y - S.y) * (y - S.y) + (z - S.z) * (z - S.z);
   if (d2 > S.rayon * S.rayon)
      return false;
   else
      return true;
}

Collision de deux sphères

Collision de 2 sphères : voyons si la distance entre les deux centres est supérieure ou inférieure à la somme des rayons.

bool Collision(Sphere S1, Sphere S2)
{
   int d2 = (S1.x - S2.x) * (S1.x - S2.x) + (S1.y - S2.y) * (S1.y - S2.y) + (S1.z - S2.z) * (S1.z - S2.z);
   if (d2 > (S1.rayon + S2.rayon) * (S1.rayon + S2.rayon))
      return false;
   else
      return true;
}