Sol

La Heigtmap (ou carte des hauteurs) est très utilisée dans les jeux 3D pour définir des sols non plats.

Définition

Considérons une généralisation de la collision sur sol 2D courbe, que nous avons vu au-dessus, mais en 3D. Rappelez-vous, l’idée était de savoir, pour tout $x$, quel était le $y$ associé avec une fonction $y = f(x)$. À partir de là, on pouvait marcher sur une courbe.

L’idée est la même ici, savoir pour un $x,y$ donné, quel est le $z$ du sol. Autrement dit de connaître $z = f(x, y)$.

Le problème, comme plus haut, est de définir cette fonction f(x,y). Afin d’avoir un contrôle des reliefs, nous allons définir cette fonction à partir d’une simple image. Et c’est cette image que nous appellerons Heigtmap.

Voici une Heightmap, en haut, et le terrain qu’elle permettra de générer, en bas. Exemple tiré de Wikipédia.

La heightmap est une image (un BMP par exemple) en noir et blanc, avec des nuances de gris. À partir de cette image, on reconstruit le sol 3D de droite.

Le concept est simple, pour un $x,y$ donné, on regarde la couleur du pixel sur le BMP. Plus le pixel est blanc, plus l’altitude à cette position est élevée.

Regardez, on voit bien que les zones noires à gauche sont représentées par des creux à droite, et les zones blanches par des pics de montagne.

La couleur du pixel à un $x,y$ donné est finalement le $z$ attendu. Nous avons donc notre fonction $z = f(x, y)$. C’est le BMP.

Applications

Beaucoup de jeux où vous pouvez marcher en extérieur dans un monde fait de relief. Beaucoup de jeux de voitures actuels sont fait avec un Heightmap.

Notez qu’on peut définir une altitude minimale (qui correspondra au pixel noir) et une altitude maximale (qui correspondra au pixel blanc) de notre choix. Cela permet de faire des dénivelés plus ou moins importants, en fonction de nos besoins. Par exemple, à gauche, le sol est peu vallonné, alors qu’il l’est énormément dans le jeu de voiture (Monster Truck).

Calcul de collision

La fonction « simple » de collision sur une HeightMap n’est pas si compliquée. Nous ne définirons pas de structure Image, nous partirons juste du principe qu’on peut demander la valeur Z (la blancheur) d’un pixel $x,y$.

Nous calculerons donc d’abord, pour une AABB3D, le point en bas au centre, de la même façon que nous l’avions fait pour le chapitre sur le sol courbe. Nous considèrerons, pour notre AABB3D, l’axe z de bas en haut.

bool Collision(AABB3D box, Image Im)
{
   float x = box.x + box.w / 2;
   float y = box.y + box.h / 2;
   float z = box.z + box.d;
   int ix = round(x);
   int iy = round(y);
   int hauteursol = GetPixel(Image, ix, iy);
   if (hauteursol > z)
      return true;
   else
      return false;
}

Cette fonction va prendre, pour un x (ou un y) donné, la valeur entière la plus proche (la fonction round) pour trouver l’altitude.

Affinage mathématique

Cette partie requiert certaines connaissances mathématiques universitaires (ou fin de lycée).

Problème de discontinuité

La fonction que nous avons vu juste au-dessus présente un inconvénient majeur, elle nous génère un « escalier ». Cela ne se voit pas trop si le terrain est « serré », c’est-à-dire s’il y a peu de distance entre $f(x, y)$ et $f(x + 1, y)$ (et de même pour $y$). Mais cela va faire de grandes cassures dans le cas contraire.

Voyons le schéma ci-dessous :

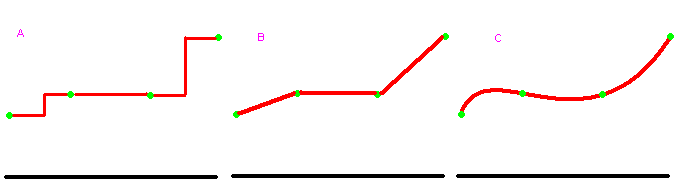
Ce que nous avons vu, c’est le cas A. Imaginez qu’on regarde une seule ligne de notre terrain, et de profil. Les points verts sont les points d’altitude, de coordonnées $x = 0$, $1$, $2$ et $3$. Les traits rouges sont les valeurs de la fonction entre $0$ et $1$, entre $1$ et $2$ et entre $2$ et $3$.

La fonction round() arrondit au nombre entier le plus proche, donc typiquement, la limite est au milieu, à $0.5$, $1.5$, $2.5$. Et c’est la que nous avons une belle cassure. Et si nous faisons ainsi avancer notre personnage, quand il atteindra la limite, il va monter ou descendre d’un coup, ce qui pourra être bien moche.

Interpolation linéaire

Si nous regardons pour le moment la courbe, cas A, nous connaissons les valeurs de $y$ que pour $x = 0$, $x = 1$, $x = 2$… Mais nous ne les connaissons pas pour $x = 1.5$ par exemple. Un calcul d’interpolation permet de trouver des valeurs correctes pour toutes les valeurs de $x$, même si $x$ est un nombre décimal.

Le principe de l’interpolation linéaire est le suivant : pour un $x$ donné, nous séparons sa partie entière de sa partie décimale comme ceci :

Par exemple, pour $x = 1.5$, nous obtenons $i = 1$ et $d = 0.5$.

La formule d’interpolation linéaire est la suivante :

Exemple : soit $f(1) = 4$, $f(2) = 5$. Nous cherchons $f(1.4)$. $i = 1$ et $d = 0.4$.

Cela fonctionne dans tous les cas, même si nous avons une valeur de $x$ entière. Nous cherchons $f(2)$. $i = 2$ et $d = 0.0$

Interpolation bilinéaire

Si nous considérons une surface $z = f(x, y)$ dont nous ne connaissons que $x$ et $y$ entiers (une Heightmap typiquement), nous pouvons calculer une interpolation avec des $x, y$ réels de la même manière. Tout d’abord, nous prenons la partie entière et décimale de $x$ et $y$.

La formule générale est similaire à celle de l’interpolation linéaire :

Cela nous donne la formule de collision suivante :

bool Collision(AABB3D box, Image Im)
{
   float x = box.x + box.w / 2;
   float y = box.y + box.h / 2;
   float z = box.z + box.d;
   int ix = (int)(x);
   int iy = (int)(y);
   float dx = x - ix;
   float dy = y - iy;
   float hauteursol = ((1 - dx) * GetPixel(Image, ix, iy) + dx * GetPixel(Image, ix + 1, iy)) * (1 - dy)
                     +((1 - dx) * GetPixel(Image, ix, iy+1) + dx * GetPixel(Image, ix + 1, iy + 1)) * dy;
   if (hauteursol > z)
      return true;
   else
      return false;
}

Interpolation cubique et bicubique

L’interpolation cubique permet un lissage beaucoup plus joli de la courbe ou de la surface (bicubique), en utilisant des polynômes de degré 3. C’est le cas C que j’ai dessiné plus haut. Je ne développerai pas cette partie complexe, je voulais juste vous informer que ça existe. C’est cependant peu utilisé dans les jeux, l’interpolation bilinéaire étant souvent suffisante.