De nos jours, le temps que passe le processeur à attendre la mémoire devient de plus en plus un problème au fil du temps. Il faut dire que la différence de vitesse entre processeur et mémoire est tellement importante que les accès à la mémoire sont très lents comparées aux instructions machines usuellement employées : alors qu'une simple addition ou multiplication va prendre entre 1 et 5 cycles d'horloge, un accès à la mémoire RAM fera plus dans les 400-1000 cycles d'horloge.
Pour limiter la casse, les processeur intègrent une mémoire cache, située entre la mémoire et le processeur. Cette mémoire a toutefois une capacité limitée à quelques mébioctets, en contrepartie d'un temps d'accès nettement moins faible.
Quand le processeur veut lire ou écrire une donnée, il va d'abord vérifier si celle-ci est dans la mémoire cache. Si c'est le cas, alors il va lire ou écrire dans le cache, ce qui sera très rapide. Mais dans le cas contraire, il devra aller chercher les données à lire ou écrire dans la mémoire : ce sera des centaines de fois plus lent que l'accès au cache, et les performances s'effondreront.
Tout ce temps sera du temps de perdu que notre processeur tentera de remplir avec des instructions ayant leurs données disponibles (dans un registre voire dans le cache si celui-ci est non-bloquant), mais cela a une efficacité limitée.
Dans ces conditions, plus on limite le nombre de cache miss (les situation où la donnée n'est pas dans le cache), meilleures sont les performances. Et à ce petit jeu, gérer correctement le cache est une nécessité, particulièrement sur les processeurs multi-cores. Bien évidement, optimiser au maximum la conception des caches et de ses circuits dédiés améliorera légèrement la situation, mais n'en attendez pas des miracles.
Non, une bonne utilisation du cache (ainsi que de la mémoire virtuelle) repose en réalité sur le programmeur qui doit prendre en compte certains principes dès la conception de ses programmes. La façon dont est conçue un programme joue énormément sur le nombre de cache miss, et donc sur les performances.
Un programmeur peut parfaitement tenir compte du cache lorsqu'il programme, et ce aussi bien au niveau :
- de son algorithme : il existe des algorithmes cache oblivious, qui tiennent compte de l'existence de la mémoire cache au niveau purement algorithmique dans les calculs de complexité ;
- du choix des structures de données : un tableau est une structure de donnée respectant le principe de localité spatiale, tandis qu'une liste chainée ou un arbre n'en sont pas (bien qu'on puisse les implémenter de façon à limiter la casse);
- du code source : par exemple, le sens de parcourt d'un tableau multidimensionnel peut faire une grosse différence ;
- ou de l'assembleur : il existe des instructions qui vont directement lire ou écrire dans la mémoire sans passer par le cache, ainsi que des instructions qui permettent de précharger une donnée dans le cache (instructions de prefetching).
Quoiqu'il en soit, il est quasiment impossible de prétendre concevoir des programmes optimisés sans tenir compte de la hiérarchie mémoire. Et cette contrainte va se faire de plus en plus forte quand on devra passer aux architectures multicœurs.
Il y a une citation qui résume bien cela, prononcée par un certain Terje Mathisen. Si vous ne le connaissez pas, cet homme est un vieux programmeur (du temps durant lequel on codait encore en assembleur), grand gourou de l’optimisation, qui a notamment travaillé sur le moteur de Quake 3 Arena.
almost all programming can be viewed as an exercise in caching
Le but de ce tutoriel est de vous expliquer les techniques qui permettent d'optimiser un programme pour la mémoire cache. Nous n'allons pas voir les optimisations au niveau de l'assembleur (qui sont inutiles), ou celles liées aux algorithmes cache oblivious (trop complexes et limitées à des cas d'utilisation trop spécifiques). Nous allons surtout aborder les optimisations de code et celles liées aux structures de données.
Diminuer l'empreinte mémoire
Il existe deux méthodes pour améliorer l'utilisation de la mémoire cache
- diminuer la quantité de mémoire utilisée pour stocker des données : moins de mémoire utilisée signifie que l'on peut mettre plus de données dans le cache, augmentant son rendement ;
- rendre les accès à la mémoire le plus consécutif possible.
Diminuer la quantité de mémoire prise par les données permet aussi d'optimiser pour la mémoire cache. Après tout, les mémoires cache d'un processeur ont une taille finie, qui varie de quelques kibioctets à quelques mébioctets. Si on diminue la taille des données, on peut en placer plus dans la mémoire cache, ce qui diminue fortement le nombre de cache miss. Et cela peut se faire de diverses manières.
Choix du type de donnée
La première solution consiste à bien choisir le type de la donnée. Dans la majorité des langages (suivant le compilateur), les types char, int, short, et autres n'utilisent pas la même quantité de mémoire. Par exemple, sur les processeurs X86 actuels, utiliser un tableau de char au lieu d'un tableau de int permet de diviser par 4 à 8 la quantité de mémoire et de cache utilisée pour le tableau.
Il est aussi possible d'utiliser intelligemment les enums, bilfields, et autres unions pour économiser de la mémoire. Mais c'est vraiment des solutions peu efficaces, qui servent quand on a vraiment rien de mieux et que l'on doit gratter des cycles. Mais il existe d'autres méthodes nettement plus efficaces.
Alignement mémoire
La première méthode concerne l'usage des structures à la C, des classes, des enregistrements, etc. En théorie, les variables d'une structure sont placées les unes après les autres en mémoire, dans leur ordre de déclaration dans la structure. Par exemple, prenons cette structure :
1 2 3 4 5 6 | struct Exemple { double flottant; char lettre; unsigned int entier; }; |
On va supposer qu'un double prend 8 octets, qu'un char en prend 1, et qu'un unsigned int en prend 4. Voici ce que donnerait cette structure en mémoire :

Logiquement, notre structure devrait prendre 8 octets pour un double, un octet pour le char, et 4 pour le unsigned int, ce qui donne un total de 13 octets. Dans la réalité, la structure va prendre 16 octets. Ce 16 ne sort pas de n'importe où et qu'il est parfaitement normal. Mais autant prévenir : l'explication va paraitre assez déroutante. On va en effet aller regarder ce qui se passe au plus profond de la mémoire !
Lorsque notre processeur va vouloir manipuler un champ de notre structure, il va d'abord commencer par la lire depuis la mémoire en utilisant le bus de donnée. Ce bus de donnée permet souvent de charger plusieurs octets depuis la mémoire. Le processeur peut ainsi charger 2, 4 ou 8 octets d'un seul coup (parfois plus). On dit que le processeur accède un mot en mémoire. Ce mot n'est rien d'autre qu'une donnée qui a la même taille que le bus de donnée.
Certains processeurs ou certaines mémoires imposent des restrictions assez drastiques dans la façon de gérer ces mots. Certains processeurs (ou certaines mémoires) regroupent les cases mémoires en "blocs" de la taille d'un mot : ceux-ci utilisent un certain alignement mémoire. On peut voir chacun de ces blocs comme une "case mémoire" fictive un peu plus grosse que les cases mémoires réelles et considérer que chacun de ces blocs possède une adresse.
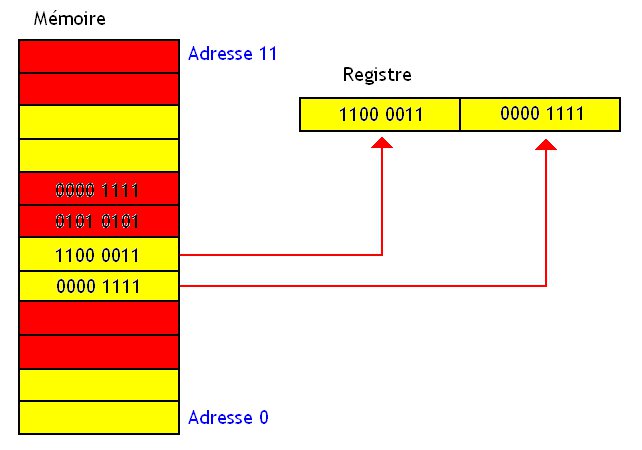
Bon, maintenant imaginons un cas particulier : je dispose d'un processeur utilisant des mots de 4 octets. Je dispose aussi d'un programme qui doit manipuler un caractère stocké sur 1 octet, un entier de 4 octets, et une donnée de 2 octets. Mais un problème se pose : le programme qui manipule ces données a été programmé par quelqu'un qui n'était pas au courant de ces histoire d'alignement, et il a répartit mes données dans la structure comme ceci :
1 2 3 4 5 6 | typedef struct Exemple { char lettre; unsigned int entier_long; short entier_court ; } Exemple; |
Supposons que cet entier soit stocké à une adresse non-multiple de 4. Par exemple :
| Adresse | Octet 4 | Octet 3 | Octet 2 | Octet 1 |
|---|---|---|---|---|
| A | Caractère | Entier | Entier | Entier |
| A + 4 | Entier | Donnée | Donnée | - |
| A + 8 | - | - | - | - |
Pour charger mon caractère dans un registre, pas de problèmes : celui-ci tient dans un mot. Il me suffit alors de charger mon mot dans un registre en utilisant une instruction de mon processeur qui charge un octet. Pour ma donnée de 2 octets, pas de problèmes non plus, vu que celui-ci est dans un mot.
Mais si je demande à mon processeur de charger mon entier, ça ne passe pas ! Mon entier est en effet stocké sur deux mots différents, et on ne peut le charger en une seule fois : mon entier n'est pas aligné en mémoire. Dans ce cas, il peut se passer des tas de choses suivant le processeur qu'on utilise.
Sur certains processeurs, la donnée est chargée en deux fois : c'est légèrement plus lent que la charger en une seule fois, mais ça passe. Mais sur d'autres processeurs, la situation devient nettement plus grave : le programme responsable de cet accès mémoire en dehors des clous se fait sauvagement planter le faciès sans la moindre sommation.
Pour éviter ce genre de choses, les compilateurs utilisés pour des langages de haut niveau préfèrent rajouter des données inutiles (on dit aussi du padding) de façon à ce que chaque donnée soit bien alignée sur le bon nombre d'octets. En reprenant notre exemple du dessus, et en notant le padding X, on obtiendrait ceci :
| Adresse | Octet 4 | Octet 3 | Octet 2 | Octet 1 |
|---|---|---|---|---|
| A | Caractère | X | X | X |
| A + 4 | Entier | Entier | Entier | Entier |
| A + 8 | Donnée | Donnée | X | X |
Ce sont ces données de padding qui ont fait passer notre structures de 13 à 16 octets. Comme quoi, l'explication était au final très simple. Évidemment, ces données de padding prennent un peu plus de place, et de la mémoire est gâchée inutilement. Même chose pour ce qui est de la mémoire cache : ces données de padding vont occuper de la mémoire cache alors qu'elles sont totalement inutiles.
Supression du padding
Une bonne optimisation consiste à diminuer la quantité d'octets utilisés pour le padding, et éventuellement de le faire disparaitre. Comme on le verra plus tard, il existe différentes méthodes pour éliminer ce padding, quelque soit le langage de programmation utilisé.
Pour le moment, nous allons nous limiter à aborder un conseil valable pour le C et le C++. Dans ces langages, on peut éviter de gaspiller de la mémoire inutilement en faisant attention à l'ordre de déclaration de nos variables. Par exemple, si on reprend l'exemple du dessus, on peut gagner 4 octets facilement. Il suffit de déclarer la structure comme ceci :
1 2 3 4 5 6 | typedef struct Exemple { unsigned int entier_long; short entier_court ; char lettre; } Exemple; |
Si on regarde bien, cette structure donnerait ceci en mémoire :
| Adresse | Octet 4 | Octet 3 | Octet 2 | Octet 1 |
|---|---|---|---|---|
| A | Entier | Entier | Entier | Entier |
| A + 4 | Donnée | Donnée | Caractère | X |
Ce qui prend seulement 8 octets au lieu de 12. Certains octets de padding ont étés éliminées. Moralité : programmeurs, si vous voulez économiser de la mémoire, faites gaffe à bien gérer l'alignement en mémoire ! Essayez toujours de déclarer vos variables de façon à remplir un mot intégralement ou le plus possible.
Attention, ce conseil n'est utile que dans des langages comme le C ou le C++. Des langages comme Java ou Python ne sont absolument pas concerné par les conseils de ce paragraphe. Si vous codez dans un langage de "très haut" niveau, passez votre chemin.
Une bonne heuristique consiste à déclarer les données dans la structure de la plus grande à la plus petite : les données qui prennent le plus d'octets doivent être placées en tout début de structure, tandis que les plus légères doivent être placées en toute fin. Mais cela ne marche que si les données ont une taille qui est une puissance de deux : avec des données de 3 ou 7 octets, cela ne peut pas marcher.
Ajouts de padding
Il faut noter que dans certains cas, il peut être avantageux d'ajouter du padding, histoire d'éviter certaines formes assez spéciales de cache miss (ces conflicts miss pour ceux qui connaissent). Mais cela ne fonctionne que dans des circonstances particulières, sur certains types de cache particuliers : les caches direct mapped et N-way Asociative. Je n'en parlerais pas tout de suite, mais je reviendrais dessus plus tard.
Éviter les doublons
Une autre méthode consiste à compresser les données de manière à éviter les doublons : il est possible de stocker plusieurs exemplaires d'une donnée assez grosse, on ne garde qu'un exemplaire, et on mémorise des pointeurs sur cette donnée à la place. Nous verrons comment utiliser cette technique dans l'implémentation des tableaux et des matrices dans la suite du tutoriel. Cette méthode ne fonctionne que pour des données assez grosses, dont la taille est largement supérieure à celle d'un pointeur.
Look-up Tables
Il arrive souvent que certains programmeurs remplacent de longues suites de calcul en précalculant toutes les valeurs possible de ces calculs : au lieu de faire les calculs, ils vont simplement aller récupérer un résultat pré-calculé depuis un tableau ou une table de hachage en mémoire.
De nos jours, les bénéfices à ce genre d'opérations deviennent de plus en plus limités (même s'il ne s'agit clairement pas d'une mauvaise méthode d’optimisation). L'usage de tables de pré-calcul est à considérer avec modération, et doit être si possible être justifié par des benchmarks ou une analyse de complexité algorithmique digne de ce nom.
Allocateurs mémoire
Dernière méthode : recoder soit-même un allocateur mémoire adapté à l'organisation en mémoire des structures de données utilisées dans le programme. Et surtout, cela demande des compétences que vous n'avez pas (moi non plus d'ailleurs).
Structures de données et accès mémoire
Notre mémoire cache aime beaucoup les données consécutives en mémoire. Il faut dire que la mémoire cache est découpée en lignes de caches, des blocs de mémoire d'environ 64 octets. Ces lignes de caches peuvent accepter une copie d'un bloc de donnée en provenance de la mémoire : toute lecture va automatiquement charger un bloc complet qui a la même taille que la ligne de cache.
Dans ces conditions, si les données sont dispersées dans la mémoire, elle auront tendance à ne pas utiliser des lignes de cache complètes : on chargera 64 octets pour remplir une ligne de cache, alors que seuls 4 à 16 octets sera utiles. Cela gâche de la mémoire cache vu qu'on n'utilise pas toute sa capacité, sans compter que cela gaspille de la bande passante mémoire.
Ensuite, il faut savoir que le processeur peut tenter de prédire quelles seront les données qui seront bientôt chargées dans le cache, et les précharger en avance. Certaines techniques de pré-chargement, ou prefetching, considèrent que les données sont consécutives en mémoire : elles consistent simplement à charger les données adjacentes aux données précédemment chargées dans le cache.
Dans ces conditions, si les accès ne sont pas consécutifs, le processeur peut se tromper dans ses prédictions, et charger des données inutiles dans le cache : cela gaspille de la mémoire cache à rien (même s'il existe des techniques pour limiter la casse comme les streams buffer ou l'usage des algorithmes de remplacement des lignes de cache LRU/LFU, voir du cache filtering), et cela gaspille de la bande passante mémoire lors du pré-chargement.
On peut tirer un conseil évident de ce qui vient d'être dit : il faut rendre les données consécutives en mémoire. Et cela passe par un choix judicieux des structures de données. Outre les considérations algorithmiques (qui ne sont clairement pas à négliger), les structures de données utilisées ont un fort impact sur l'utilisation du cache.
Évidemment, qui dit données consécutives en mémoire dit tableaux. Cependant, il faut aussi mentionner le fait que certaines structures de données peuvent être linéarisées, en les transformant partiellement en tableaux tout en conservant leurs complexités algorithmiques usuelles. Il existe de nombreuses structures de données dites cache oblivious, qui utilisent la mémoire cache de manière optimale quelque soit l'ordinateur. Et ces structures de données ne sont pas encore disponibles dans la majorité des langages de programmation actuels : par exemple, la STL manque d'une simple liste chainée optimisée pour le cache.
Tableaux unidimensionnels
Vu ce que l'on vient de dire, il est évident que parcourir des tableaux dans l'ordre est nettement plus efficace que de les parcourir dans le désordre. Ce principe, qui veut que les parcours séquentiels sont plus rapides que les accès aléatoires est trivial, et il est parfois possible de réécrire un algorithme de manière à remplacer des accès aléatoires par des accès séquentiels. Un exemple assez impressionnant est mentionné dans le .pdf suivant : Pitfalls of object oriented programmaing.
De même, il est possible de faire quelques optimisations assez simples sur la manière dont on parcourt les tableaux. Par exemple, on peut parfois fusionner des boucles qui parcourent un même tableau. Il est aussi possible de couper une boucle en deux, si jamais celle-ci parcourt deux tableaux de telle sorte que les actions effectuées sur un tableau n'influencent pas ce qui se fait sur l'autre. Mais ces optimisations sont automatiquement effectuées par les compilateurs modernes.
En dehors de ce conseil, on pourrait croire que les tableaux uni-dimensionnels ne peuvent pas être optimisés pour la mémoire cache : ceux-ci ont déjà une occupation mémoire minimale, et des données consécutives. Pour les tableaux de données primitives, comme les int, char, float, double, etc, c'est vrai. Mais pour les tableaux de structures ou d'objets, ce n'est pas le cas.
Tableaux de structures
D'ordinaire, les programmeurs ont tendance à rassembler plusieurs structures dans des tableaux (ils peuvent aussi utiliser d'autres structures de données selon leurs besoins, mais passons).
Cependant, toutes les données d'une structure ne sont pas utiles en même temps et vous n'avez pas toujours besoin de tous les champs : seule une partie des champs est accédée et modifiée, tandis que certains champs sont laissés intacts. Certains champs de la structure sont fréquemment accédés ensemble, tandis que d'autres champs sont assez peu utiles.
Avec un tableau de structure, tous les champs d'une structure sont chargés dans le cache, même ceux qui sont inutiles. Pour éviter cela, on peut utiliser la technique du Hot/cold spilting. Celle-ci consiste à séparer les données fréquemment utilisées des données peu fréquemment utilisées dans des structures séparées. La première structure contiendra les données les plus fréquemment utilisées, ainsi qu'un pointeur vers l'autre structure. Cette autre structure contiendra les champs restants, peut fréquemment utilisées, et éventuellement un pointeur vers la première structure.
Avec cette technique, la parcours d'un tableau de structure ne chargera que la structure qui contient les données les plus fréquemment utilisées. Les autres données ne seront chargées que si le besoin s'en fait sentir, en passant par l'intermédiaire de la première structure.
Structures de tableaux
Cependant, il existe une organisation alternative, qui donne de meilleurs résultats du point de vue de la mémoire cache, et qui est systématiquement conseillée dans les guides d'optimisations publiés par Intel et AMD : utiliser des structures de tableaux en lieu et place de tableaux de structures.
Cependant, il faut préciser quelque chose sur cette différence entre SoA (structure of array) et AoS (array of structure) : cette méthode ne donne de bons résultats pour des données qui sont relativement grosses. Plus précisément, si le tableau tout entier arrive à tenir dans la mémoire cache de niveau L1/L2, l'amélioration ne sera pas spectaculaire, et vous risquez même d'obtenir une baisse de performances dans certains cas. Par contre, si les données sont suffisamment grosses, vous obtiendrez systématiquement un gain.
Reprenons cette structure d'exemple, et créons un tableau de 1500000 de ces structures :
1 2 3 4 5 6 7 | typedef struct Exemple { unsigned int entier_long; char lettre; } Exemple; Exemple tableau[1500000] ; |
Si l'on crée un tableau de 1500000 structures de type Exemple, le compilateur va automatiquement insérer du padding dans chaque structure. Ce qui fait que le char d'une structure sera séparé du int de la structure suivante par du padding, qui prendra inutilement de la mémoire cache.
A la place, il est recommandé de ne pas utiliser un tableau, mais plusieurs : un par champ de la structure. Dans l'exemple du dessus, on devrait utiliser deux tableaux de 1500000 éléments : un tableau qui stocke les int de chaque structure, et un autre pour les char.
1 2 3 4 5 | typedef struct Tableau_Exemple { unsigned * tableau_entiers ; char * tableau_lettre; } Tableau_Exemple; |
En faisant cela, les int sont alignés en mémoire sans qu'il y aie besoin de padding, et c'est la même chose pour les char : le padding disparait.
De plus, quand vous parcourez une structure, vous n'avez pas toujours besoin de tous les champs : seule une partie des champs est accédée et modifiée, tandis que certains champs sont laissés intacts. Avec un tableau de structure, tous les champs d'une structure sont chargés dans le cache. Mais ce n'est pas le cas avec une structure de tableau : seul les tableaux des champs utiles sont parcours, pas les autres. L'économie en cache et en bande passante mémoire est donc appréciable.
Sous certaines conditions, il vaut donc mieux utiliser plusieurs tableaux regroupés dans une seule structure, avec un tableau pour chaque champ de la structure. Les conditions pour cela sont simples :
- un faible nombre de champs doit être visité lors du parcours des tableaux ;
- la taille du tableau doit être suffisante pour dépasser la taille du cache ;
- les accès au tableau doivent être des accès séquentiels.
Cette technique permet d'économiser de la mémoire, et donne de bons résultats quel que soit le cache, ou les algorithmes de prefetching utilisés par le processeur. Les gains peuvent être assez impressionnant : on peut doubler, voire tripler la vitesse de votre code source.
Cette technique peut aussi s'appliquer aux tableaux multidimensionnels et aux matrices, même si le gain est clairement moindre.
Tableaux unidimensionnels versus multidimensionnels
On peut aussi citer le fait que, pour des raisons relativement techniques (liées à l’associativité du cache), il est préférable de regrouper des tableaux unidimensionnels séparés dans un seul tableau multidimensionnel. Ainsi, on peut transformer une structure de tableaux en un seul tableau multidimensionnel sans problèmes.
Mais évidemment, cela ne marche pas toujours : il faut que les données soient de même type. A défaut, certains n'hésiteront pas à contourner cette contrainte en utilisant des unions, mais je ne conseille pas cette pratique.
Tableaux de pointeurs
Dans la majorité des langages objets, ces tableaux qui contiennent des objets (des types non-primitifs) sont simplement des tableaux de références, soit des tableaux de pointeurs (oui, j'ai dit pointeur, et si ça ne vous plaît pas, c'est le même tarif). En conséquence, les objets ne sont pas absolument pas consécutifs en mémoire.
Selon quelques études faites sur le sujet, c'est une des raisons qui fait que le Java est plus lent que le C. Il y a surement moyen d'éviter cela, en utilisant les constructions du langage, mais je ne les connais malheureusement pas.
Cependant, il existe des situations où utiliser des tableaux de pointeur donne un avantage certain en terme de performances : cela permet de ne pas dupliquer des données. Prenons un tableau de structures, ces structures étant assez grosses. Il arrive parfois que certaines structures soient identiques : la même structure est présente plusieurs fois dans le tableau, à des indices différents. Dans ce cas, il vaudrait mieux n'utiliser qu'un seul exemplaire de cette structure, pour diminuer l'occupation de la mémoire.
Dans ce cas, les tableaux de pointeurs permettent d'éviter de tels doublons. Il suffit d'utiliser un tableau de structure dans lequel les structures ne sont présentes qu'en un seul exemplaire (sans doublons), et un second tableau de pointeur. Le tableau de pointeur sert à effectuer la correspondance indice -> pointeur vers la structure demandée. A partir de ce pointeur, on peut alors accéder à la structure voulue. Cette organisation est ce qu'on appelle un vecteur de Liffe.
Ces vecteurs de Liffe permettent donc de diminuer l'occupation de la mémoire, en évitant les doublons. L’avantage est clair en terme de cache. De plus, le premier accès à une structure va charger celle-ci en cache : les accès suivants à cette structure peuvent être améliorés si jamais la donnée est encore en cache lors de ceux-ci. Avec un tableau de structure, chaque accès à une structure va charger celle-ci depuis la mémoire.
Cette technique peut aussi s'appliquer aux tableaux multidimensionnels et aux matrices : on obtient alors des matrices creuses.
Tableaux multi-dimensionnels et matrices
Les tableaux multi-dimensionnels sont une première source d'optimisation de ce point de vue. En effet, l'organisation des données d'un tableau multi-dimensionnel dépend fortement du langage.
Row et Column Major Order
Prenons le tableau à deux dimensions suivant :
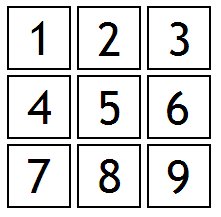
Comme vous le voyez, il s'agit d'un tableau d'entiers, à deux dimensions, comprenant trois lignes et trois colonnes.
Dans certains langages, comme le C, le C++ ou le FORTRAN, toutes les données du tableau sont stockées les unes à coté des autres en mémoire. En clair, les données stockées dans un tableau à plusieurs dimensions sont rassemblées dans un tableau à une seule dimension : les lignes ou les colonnes d'un tableau multidimensionnel sont stockées les unes à la suite des autres.
Ceci dit, il nous reste un petit détail à régler. Si je prends le tableau au-dessus, je peux parfaitement stocker celui-ci dans un seul tableau, mais deux deux façons différentes. Je peux tout stocker dans un tableau en mettant les colonnes les unes après les autres.

C'est cette solution qui est utilisée dans des langages de programmation comme FORTRAN, mais ce n'est pas le cas en C. En C, nos tableaux sont stockés lignes par lignes.

La morale, c'est que l'on observera de grosses différences de performances suivant que l'on parcourt un tableau lignes par lignes ou colonnes par colonnes. En C, le parcours ligne par ligne sera nettement plus rapide, vu que les lignes sont placées les unes après les autres, on accèdera à des données consécutives en mémoire : le parcours se résumera en un simple parcours de tableau unidimensionnel. Par contre, le parcours colonne par colonne ne permettra pas d’accéder à des données consécutive : deux colonnes consécutives ne se suivent pas en mémoire, et les performances seront désastreuses.
Un bon exemple est celui de la multiplication de deux matrices. Lors du calcul de A fois B, la matrice A est parcourue ligne par ligne tandis que l'autre l'est colonne par colonne. Dans ces conditions, il vaut mieux faire en sorte que la matrice A soit stockée ligne par ligne, tandis que l'autre l'est colonne par colonne. Dans ces conditions, avec un algorithme de calcul adapté pour obtenir le bon résultat, on peut obtenir des gains de performances.
Il faut noter que, comme pour les tableaux unidimensionnels, les performances ne seront pas les mêmes entre une structure de tableaux multidimensionnels comparé à un tableau multidimensionnel de structures.
Tiled Layout
Si la majorité des langages se base sur un stockage ligne par ligne ou colonne par colonne, des chercheurs ont inventé des matrices qui ne se basent pas sur ce genre de principes. Il existe de nombreuses organisations, comme les matrices de Morton. Évidemment, les algorithmes qui manipulent ces matrices doivent être adaptés pour tenir compte de l'ordre des données en mémoire. Le principe est de découper les matrices en sous-matrices et de stocker celles-ci en mémoire les unes à la suite des autres.
L'astuce qui se cache derrière ces matrices est celui qui est à l'origine de tous les algorithmes optimisés pour le cache. Ces algorithmes sont des algorithmes diviser pour régner récursifs : ils décomposent un problème en sous-problèmes identiques, mais qui agissent sur une portion de la donnée originale. Au lieu de traiter toute la donnée d'un coup, on la traite partie par partie avant de fusionner les résultats obtenus avec chaque portion de la donnée.
L'astuce, c'est qu'une donnée complète (ici, la matrice complète) ne tient pas totalement dans le cache, ce qui est la cause de nombreux cache miss. Par contre, une sous-donnée peut tenir complètement dans le cache, ce qui rend son traitement particulièrement rapide. Dans notre exemple, une matrice complète a peu de chance de tenir dans le cache, alors qu'une sous-matrice peut. Donc, si on sait découper.
Évidemment, ces algorithmes donnent de meilleurs résultats si les données sont organisées de manière à faciliter l'implémentation de ces algorithmes. Par exemple, un algorithme de recherche dichotomique doit agir sur un tableau trié, de même qu'un algorithme de multiplication de matrice récursif, qui agit sous-matrice par sous-matrice gagne clairement à avoir des matrices explicitement découpées en sous-matrices. Et c'est le but des organisations de matrice qui vont suivre.
Commençons par les matrices 4D. Avec ces structures de données, la matrice à stocker est découpée en sous-matrices rectangulaires, de hauteur M et de largeur N. Ces sous-matrices sont mémorisées en mémoire comme une matrice normale, soit ligne par ligne, soit colonne par colonne. Ces sous-matrices sont placées les unes à la suite des autres en mémoire.
Là encore, il y a deux possibilités pour le stockage des sous-matrices : en ligne ou en colonne.
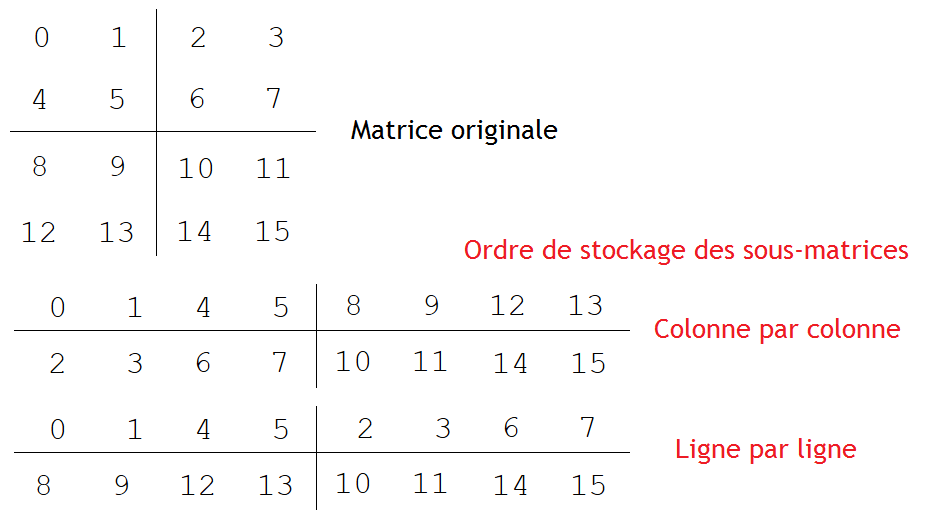
Les sous-matrices doivent avoir une taille optimale pour obtenir les meilleures performances. Dans les faits, chaque sous-matrice doit tenir dans le cache du processeur, et doit voir sa taille varier suivant la quantité de données qui peuvent être stockées dans une ligne de cache. Or, cette taille n'est pas connue, et dépend de nombreux paramètres qui dépendent de l'ordinateur. On peut donc optimiser la taille des matrices pour un ordinateur en particulier, mais sans obtenir un résultat optimal sur toutes les architectures.
Les matrices de Morton permettent de résoudre ce problème. Dans celle-ci, la matrice est découpée en 4 sous-matrice de même largeur et longueur. Ces 4 sous-matrices sont stockées dans cet ordre dans la mémoire :
- d'abord la matrice en haut à gauche ;
- puis celle en haut à droite ;
- puis celle en bas à gauche ;
- puis celle en bas à droite.
Puis, chaque sous-matrice subit le même sort, et la même procédure est appliquée de manière récursive. On arrête lorsque la matrice obtenue ne contient qu'un seul élément.
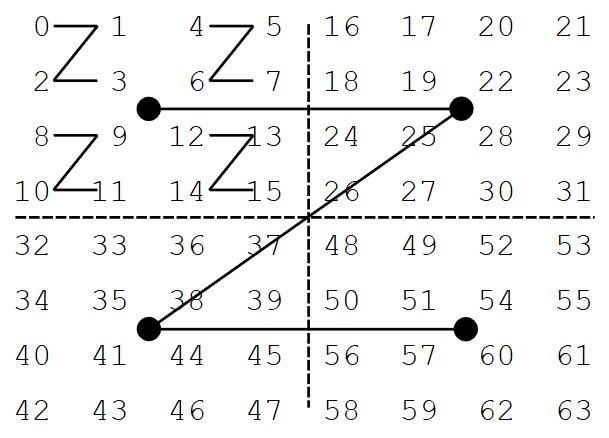
On peut trouver d'autres organisations, comme dans les matrices de Hilbert (basées sur la courbe de Hilbert) ou de Gray-Morton, qui se différencient par l'ordre de stockage des sous-matrices.
Cette organisation récursive est clairement un atout qui permet de ne pas avoir à se soucier de la taille optimale des sous-matrices : quelque soit la taille du cache, on trouvera forcément une sous-matrice qui aura la taille adéquate.
Listes chainées
Du point de vu de la mémoire cache, les listes chainées sont relativement mauvaises. Parcourir une liste chainée pour recherche un élément est relativement lent : les données sont dispersées en mémoire, ce qui fait que chaque nœud de la liste donne un cache miss. Le nombre de cache miss total est donc proportionnel au nombre de nœuds : si l'on note n le nombre d’éléments dans la liste, on obtient un nombre de cache miss en O(n).
En comparaison, le parcours d'un tableau est nettement plus économe. Si on oublie l'existence des algorithmes de préchargement, le nombre de cache miss est divisé par un facteur constant relativement élevè : on charge plusieurs éléments à la fois dans une seule ligne de cache, au lieu d'un élément par nœud pour une liste. Et si on rajoute les algorithmes de prefetching, les situations où le nombre de cache miss tombe à zéro est particulièrement élevé : ces algorithmes font passer la complexité en nombre de cache miss de O(n) à 0(1) !
Unrolled Linked List et variantes
Dans ces conditions, linéariser les listes chainées est une bonne chose. Et cela peut être fait de plusieurs manières.
Dans certains langages, comme le LISP, les listes sont implémentées en utilisant ce qu'on appelle le CDR coding. Mais cette méthode n'est clairement pas facile à utiliser dans des langages non-fonctionnels (il vaut mieux avoir des listes immutables avec ce CDR coding).
Une seconde solution, nettement plus utilisable, consiste à mémoriser plusieurs éléments par nœud dans la liste. En clair : la liste chainée est transformée en une liste de tableaux, chaque tableau correspondant à un nœud de la liste. On obtient alors une unrolled linked list.
Dans la majorité des implémentations, chaque nœud de la liste a une taille finie : tous les tableaux ont la même taille, qui est généralement celle d'une ligne de cache. Seulement, il n'est pas obligatoire que les tableaux soient totalement remplis.

A chaque nœud, on doit donc non seulement stocker le tableau et le pointeur vers le nœud suivant, mais aussi le nombre de cases du tableau qui contiennent quelque chose.
L'accès à un élément bien précis dans la liste demande donc de tenir compte du nombre d’éléments présent dans un tableau, ce qui complique le code de parcours d'une telle liste. L'insertion et la suppression d'un élément est aussi nettement plus compliquée pour les mêmes raisons. Reste à implémenter tout cela.
Packed Memory Array
Une autre solution consiste à remplacer les listes par ce qu'on appelle un Packed Memory Array. Il s'agit d'un tableau dans lequel on laisse des "trous" entre deux éléments successifs : cela permet de supporter des insertions et suppressions de données relativement rapides.
Des versions améliorées ont étés proposées dans les articles suivants :
Arbres binaires
Les arbres peuvent aussi être adaptés pour tenir compte du cache. Reste qu'il existe un grand nombre d'implémentations : entre les arbres binaires, les AVLs, les arbres rouge-noir, etc; on peut rapidement s'y perdre. Tous les types d'arbre n'ont pas les mêmes effets sur la mémoire cache, et c'est sans compter l'implémentation de ces arbres.
Implémentation naïve avec un tableau
Commençons par le plus simple : les arbres binaires (non-triés, pour commencer). Ceux-ci peuvent être implémentés avec un simple tableau, réduisant la dispersion des données en mémoire, et éliminant les pointeurs (qui pompent de la mémoire et nuisent à un alignement correct des nœuds de l'arbre en mémoire). Sur le principe, il suffit de faire comme ceci :
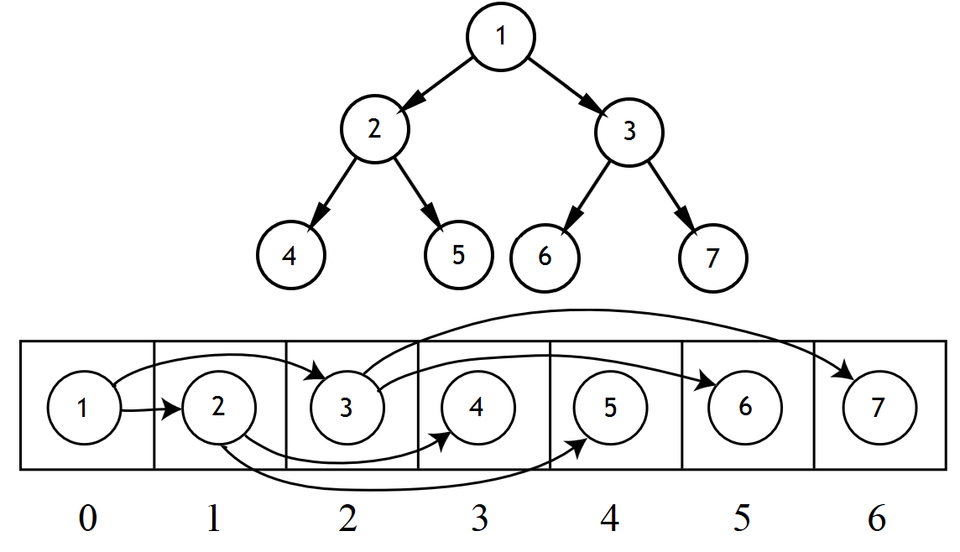
Autant dire que cette implémentation est idéale pour les parcours en largeur, qui se réduisent en une simple boucle qui parcourt le tableau dans l'ordre séquentiel. Avec l'implémentation usuelle, on se retrouve avec un cache miss pour chaque nœud de l'arbre : la complexité en défauts de cache est donc en O(n). Alors qu'avec l'implémentation sous forme de tableau, le nombre de cache miss tombe à zéro sur du matériel moderne.
Pour les parcours en profondeur, cette organisation permet de diminuer le nombre de cache miss, mais il ne faut pas trop en attendre : cela permet de diminuer la quantité de cache miss d'un facteur constant.
Van Emde Boas Layout
Il existe une autre solution pour stocker les arbres binaires avec un tableau : utiliser ce qu'on appelle le layout de Van Emde Boas. Avec lui, l'arbre est toujours stocké en mémoire dans un tableau, mais la répartition des données dans le tableau est différente : l'arbre est découpé en sous-arbres, de manière récursive.
Le principe consiste à décomposer l'arbre en sous-arbres, qui sont eux-mêmes décomposés en sous-arbres, et ainsi de suite. Ainsi, il arrivera un moment où un sous-arbre pourra tenir tout seul dans le cache (ou dans une ligne de cache). C'est encore le principe du diviser pour régner récursif, appliqué aux structures de données. Reste à voir comment appliquer ce principe aux arbres binaires de recherche.
Prenons un arbre contenant N éléments, qui est de hauteur H. On supposera que la hauteur est une puissance de deux (si ce n'est pas le cas, prendre la puissance de deux supérieure). L'idée est de couper l'arbre à mi-hauteur en deux morceaux. Le premier morceau est celui qui contient la racine, de hauteur H/2, qui contient $\sqrt{N}$ nœuds. L'autre morceau est composé de $2^{H/2}$ sous-arbres : chaque feuille du premier sous-arbre sert de racine à chacun de ces sous-arbre.
Tout les sous-arbres sont alors mémorisés les uns à la suite des autres dans le tableau :
- d'abord on place le sous-arbre qui contient la racine ;
- puis on place successivement chacun des sous-arbre du second morceau, en partant de gauche à droite.
Chacun de ces sous-arbre est décomposé en suivant le même principe, récursivement. Le découpage s’arrête une fois que l'on obtient un arbre de taille 1.
B-Tree
Une autre sorte d'arbre permet d'utiliser le cache d'une manière un peu plus efficace : les B-tree, et leurs descendants (B+tree, B-tree, etc). Les B-tree sont un équivalent des unrolled linked lists pour les arbres binaire de recherche.
Avec un B-tree, chaque nœud contient plusieurs informations. En quelque sorte, chaque nœud de l'arbre est un tableau qui contient N informations différentes. Pour chaque nœud, on trouve plusieurs fils : si un nœud contient N données, alors celui-ci a N + 1 fils. Pour faire simple, chaque donnée est insérée entre deux fils. Le fil de gauche est inférieur à la donnée, tandis que celle de droite est supérieure.
L'idée est de faire en sorte qu'un nœud permette de remplir une ligne de cache complète : l'ensemble données + pointeur vers les fils doit totalement remplir une ligne de cache. Évidemment, cela demande de connaitre la taille d'une ligne de cache à l'avance pour obtenir des performances optimales, mais une valeur approximative, moyenne, peut suffire pour la majorité des applications.
Il existe cependant des B-tree qui sont configurés pour optimiser le cache de manière optimale quelque soit la taille d'une ligne de cache. On parle alors de B-tree cache oblivious. Quand une structure de donnée fonctionne de manière optimale (du point de vue de la complexité de cache miss), on dit qu'elle est cache oblivious.
Ces implémentations sont détaillées dans les papiers de recherche suivants :
- Cache obliviousB-tree ;
- Cache oblivious dynamic search tree ;
- Cache-Oblivious Streaming B-trees ;
- Concurrent Cache-Oblivious B-Trees ;
- Cache-Oblivious String B-trees.
Files à priorité
Il existe aussi des implémentations de structures de données cache oblivious pour les files à priorité :
- Cache-Oblivious Priorit y Queue and Graph Algorithm Applications ;
- Funnel heap : a cache oblivious priority queue.
Programmes et instructions
Si les caches de données sont importants, il ne faut pas oublier le cache d'instruction. Dans certaines applications, près de la moitié des cache miss provient du cache d'instruction. Pour éviter cela, on peut penser à diminuer la taille du programme, la taille du code. Malheureusement, les programmeurs ne peuvent pas faire grand chose à ce sujet, et doivent laisser ce genre d'optimisations au compilateur. Par contre, les programmeurs peuvent faire quelques optimisations concernant leur code.
En règle générale, plus un code est linéaire, mieux c'est pour le cache d'instruction. Les algorithmes matériels de préchargement sont assez bien faits, et fonctionnent particulièrement bien avec du code très linéaire.
Par contre, les sauts ont souvent une fâcheuse tendance à causer pas mal de cache miss : leur destination est souvent inconnue (même si les algorithmes de préchargement peuvent parfois agir de concert avec la prédiction de branchement, le résultat est souvent connu trop tard). Dans ces situations, le code vers lequel le processeur va brancher n'est pas dans le cache et n'a pas pu être préchargé.
Branch Free Code
La morale, c'est qu'il vaut mieux éviter les sauts dans le code et éviter les branchements au maximum. Une première solution consiste à utiliser du branch free code, savoir supprimer des branchements en utilisant des astuces arithmétiques. Pour en savoir plus, sachez que j'ai déjà écrit un tutoriel sur ce site, disponible via ce lien : Branche Free Code et opérations bit à bit.
Fonctions longues
Une autre solution est d'utiliser des fonctions longues : cela permet d'éviter de nombreux appels de fonctions, qui comptent parmi les sauts les plus problématiques. Et cela a de nombreux autres avantages en terme de performance, et de lisibilité de code source.







