Vous connaissez le langage Python et vous avez envie de l’utiliser pour dessiner ou pour faire des graphiques et dessins.
Ici, nous verrons rapidement le module pyplot de la bibliothèque matplotlib qui nous permettra de faire des graphes.
Pour cela, nous allons nous donner un objectif : créer une fonction qui nous permettra de tracer la courbe représentative de n’importe quelle fonction passée en paramètre.
Nous allons donc introduire tout le long du tutoriel les fonctionnalités du module pour finir par faire notre super fonction.
Prérequis
Connaissance des bases du Python (un tutoriel est disponible ici).
Objectifs
Présenter rapidement le module pyplot en apprenant à tracer des courbes de fonctions mathématiques.
Le module matplotlib
matplotlib.pyplot, le module qu’il nous faut
Commençons par le début, présentons matplotlib. Il s’agit sûrement de l’une des bibliothèques python les plus utilisées pour représenter des graphiques en 2D. Elle permet de produire une grande variété de graphiques et ils sont de grande qualité.
Le module pyplot de matplotlib est l’un de ses principaux modules. Il regroupe un grand nombre de fonctions qui servent à créer des graphiques et les personnaliser (travailler sur les axes, le type de graphique, sa forme et même rajouter du texte). Avec lui, nous avons déjà de quoi faire de belles choses.
Le fonctionnement de matplotlib est très semblable à celui de matlab. Le fonctionnement, et même les noms des fonctions par exemple, sont quasiment toujours les mêmes.
Il est maintenant temps de l’installer.
Installation sous Linux
C’est sans doute sous Linux que matplotlib est le plus simple à installer. Il suffit d’utiliser son gestionnaire de paquets (en ligne de commande ou en graphique). Voici quelques exemples de commande d’installation.
sudo pacman -S python-matplotlib # Sous Arch linux
sudo apt-get install python-matplotlib # Sous Ubuntu
Utiliser le gestionnaire de paquets est la méthode la plus simple mais nous pouvons également utiliser le programme pip (qui est souvent installé par défaut) en entrant cette commande dans un terminal. Nous commençons par le mettre à jour avec la première ligne, avant d’installer matplotlib avec la seconde.
python3 -m pip install --user -U --upgrade pip
python3 -m pip install --user -U matplotlib
Il se chargera d’installer toutes les dépendances nécessaires au bon fonctionnement de matplotlib.
Installation sous Windows
Sous Windows, nous pouvons également utiliser pip pour installer matplotlib. Il nous suffit donc d’ouvrir un terminal et d’entrer ces deux commandes. La première commande permet de mettre à jour pip et la seconde installe matplotlib.
py -m pip install --user -U --upgrade pip
py -m pip install --user -U matplotlib
Les premiers tracés
Ouvrir une fenêtre
Tout d’abord, importons le module pyplot. La plupart des gens ont l’habitude de l’importer en tant que plt et nous ne dérogerons pas à la règle. On place donc cette ligne au début de notre fichier.
import matplotlib.pyplot as plt
La première commande que nous allons voir dans ce module s’appelle show. Elle permet tout simplement d’afficher un graphique dans une fenêtre. Par défaut, celui-ci est vide. Nous devrons utiliser d’autres commandes pour définir ce que nous voulons afficher.
La seconde commande, close sert tout simplement à fermer la fenêtre qui s’est ouverte avec show. Lorsque nous appuyons sur la croix de notre fenêtre, celle-ci se ferme également. Néanmoins, il vaut mieux toujours utiliser close.
Finalement, voici notre premier code.
import matplotlib.pyplot as plt
plt.show()
plt.close()
Mais, il fait rien le code. Qu’est-ce qui se passe ?
En fait, la commande show sert bien à ouvrir la fenêtre, à « show » donc montrer ce que l’on a fait précédemment. Mais nous n’avons rien fait. Nous devons alors introduire une troisième commande, la commande plot. Finalement, voici notre vrai premier code.
import matplotlib.pyplot as plt
plt.plot()
plt.show()
plt.close()
Voilà, notre fenêtre s’ouvre bien devant nos yeux émerveillés. Nous pouvons regarder les options offertes par la fenêtre dans le menu horizontal (zoom, déplacement, enregistrement en tant qu’image…).
La fonction show est bloquante. Tant que la fenêtre n’a pas été fermée, le reste du code ne s’exécute pas.
Tracer des lignes brisées
Pour tracer des lignes, nous devons utiliser la commande plot du module pyplot. Elle peut ne prendre aucun argument comme nous venons de le voir, mais c’est bien avec des arguments qu’elle est utile. En effet, si nous lui passons une liste [a, b, c] en argument, elle reliera le points A(0, a) au point B(1, b) et ce point B au point C(2, c). En fait, nous fournissons les ordonnées dans une liste, et les abscisses, elles, sont automatiquement générées et vont de 0 à len(liste) - 1. Ainsi, le code suivant…
import matplotlib.pyplot as plt
plt.plot([0, 1, 2])
plt.show()
plt.close()
… Permet d’obtenir la droite passant par les points A(0, 0), B(1, 1) et C(2, 2).
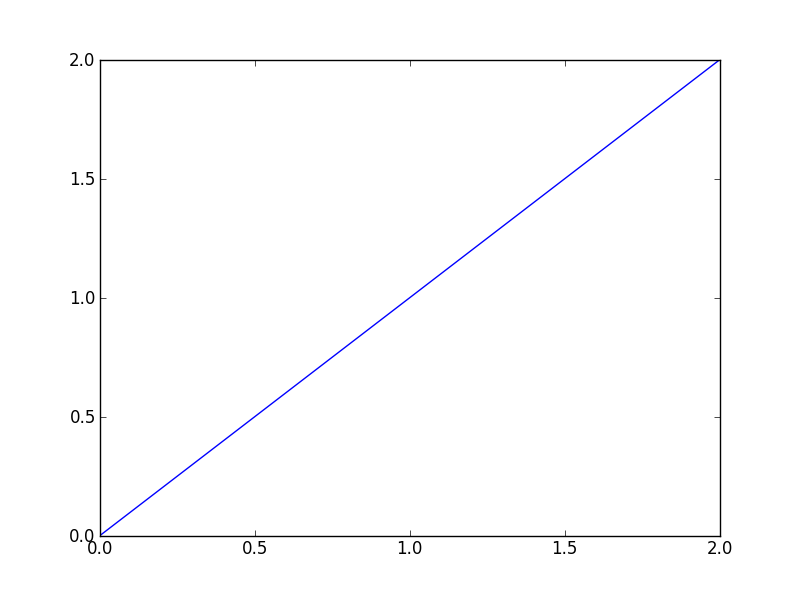
Au contraire, le code…
import matplotlib.pyplot as plt
plt.plot([1, 0, 2])
plt.show()
plt.close()
… Permet d’obtenir la droite passant par les points A(0, 1), B(1, 0) et C(2, 2).
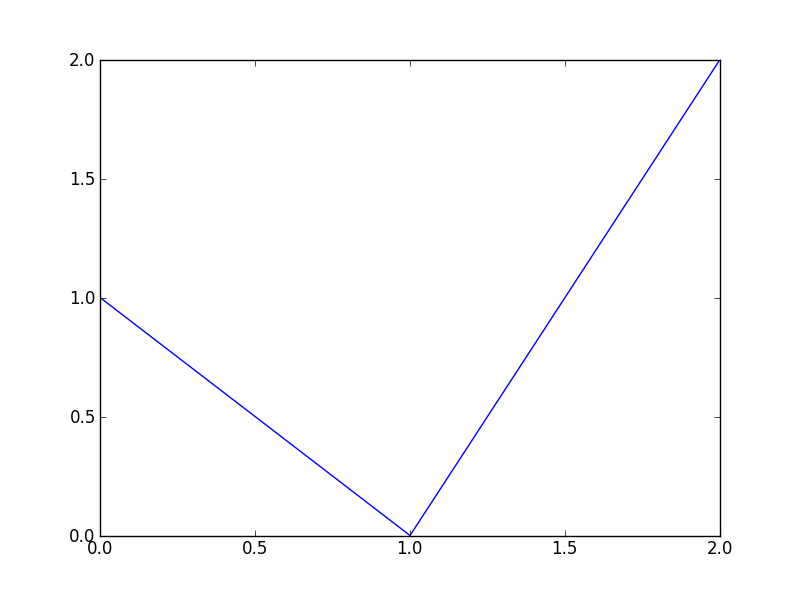
Notons l’existence de la fonction savefig qui permet de sauvegarder le graphique dans un fichier. Elle prend tout simplement en paramètre le chemin (relatif ou absolu) où il faut enregistrer le fichier. Plusieurs formats sont supportés, notamment le PDF et le PNG. Pour enregistrer le graphique, nous pouvons alors écrire ce code.
import matplotlib.pyplot as plt
plt.plot([1, 0, 2])
plt.savefig("graphique.png")
Tracer une figure
Cependant, nous pouvons aussi passer deux listes en arguments à plot. La première liste correspondra à la liste des abscisses des points que nous voulons relier et la seconde à la liste de leurs ordonnées. Ainsi, notre code précédent pourrait être le suivant.
import matplotlib.pyplot as plt
x = [0, 1, 2]
y = [1, 0, 2]
plt.plot(x, y)
plt.show()
plt.close()
Ceci nous permet alors de revenir au point de départ et de relier le dernier point au premier. Grâce à cela, nous pouvons dessiner des figures géométriques très facilement.
Essayons donc de dessiner le triangle ABC avec A(0, 0), B(1, 1) et C(-1, 1).
import matplotlib.pyplot as plt
x = [0, 1, -1]
y = [0, 1, 1]
plt.plot(x, y)
plt.show()
plt.close()
Et nous avons obtenu l’image suivante.
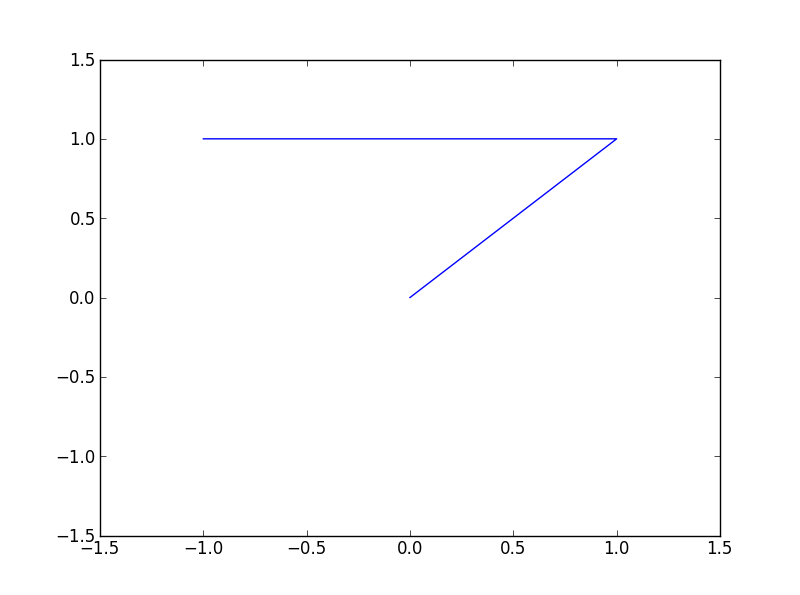
Pas très fermé comme triangle, hein ! En fait, c’est tout bête. Chaque point est relié au point le précédent ; donc, avec ce que nous avons écrit, nous ne relions pas le dernier point au premier. Il nous faut donc faire comme ça.
import matplotlib.pyplot as plt
x = [0, 1, -1, 0]
y = [0, 1, 1, 0]
plt.plot(x, y)
plt.show()
plt.close()
Et là, nous voyons apparaître notre triangle.
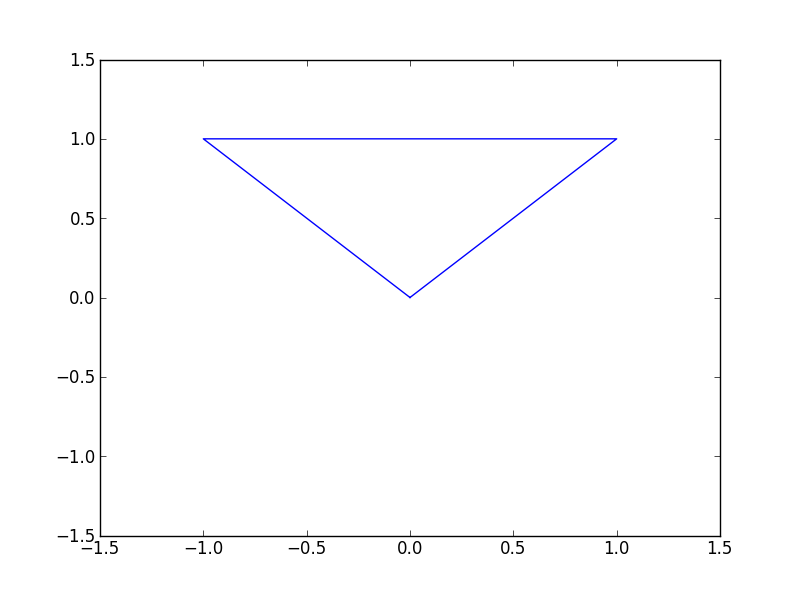
Nous pouvons également passer en paramètre à plot plusieurs listes pour avoir plusieurs tracés. Par exemple avec ce code…
import matplotlib.pyplot as plt
x = [0, 1, 0]
y = [0, 1, 2]
x1 = [0, 2, 0]
y1 = [2, 1, 0]
x2 = [0, 1, 2]
y2 = [0, 1, 2]
plt.plot(x, y, x1, y1, x2, y2)
plt.show()
plt.close()
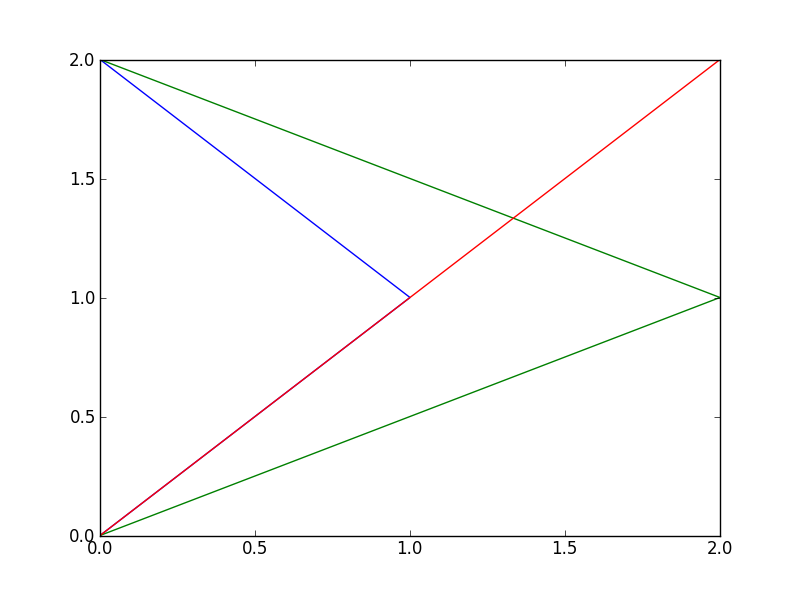
… Nous obtenons trois figures en une. Nous aurions également pu obtenir ce résultat en utilisant trois fois la commande plot avant d’utiliser la commande show.
import matplotlib.pyplot as plt
x = [0, 1, 0]
y = [0, 1, 2]
x1 = [0, 2, 0]
y1 = [2, 1, 0]
x2 = [0, 1, 2]
y2 = [0, 1, 2]
plt.plot(x, y)
plt.plot(x1, y1)
plt.plot(x2, y2)
plt.show()
plt.close()
Le résultat reste le même.
Amusons-nous un moment, dessinons des carrés, des losanges, des triangles… Et habituons-nous aux commandes.
Paramètres supplémentaires
C’est bien beau et tout ce qu’on a fait, mais nous avons parlé de personnalisation des graphiques. Il serait temps d’en parler. Et oui, c’est l’heure de voir quelques moyens de personnalisation.
Tout d’abord, pour rajouter un titre au graphique, il suffit d’utiliser la commande title en lui envoyant comme paramètre une chaîne de caractères.
Ensuite, la commande plot possède plusieurs autres paramètres. Voyons quelques-uns d’entre eux rapidement.
Dans le même genre que le titre, le paramètre label permet de légender un graphique, c’est-à-dire d’attribuer un nom à une courbe. Il suffit alors de choisir d’afficher la légende avec la commande legend qui est à placer juste avant show. Essayons-la et observons le rendu. La légende est affichée en haut à droite.
Notons qu’il est possible d’utiliser LaTeX pour écrire des mathématiques dans nos textes avec matplotlib. Par exemple, nous pouvons avoir le titre title = '$\alpha = f(\beta)$'. (Pour en savoir plus sur l’utilisation des mathématiques avec LaTeX, nous pouvons lire ce tutoriel).
color
Le paramètre color permet de changer la couleur du tracé. Cette couleur peut être donnée sous plusieurs formes.
- Sous forme de chaîne de caractères représentant les noms (ou abréviations) pour les couleurs primaires, le noir et le blanc :
boublue,gougreen,roured,coucyan,moumagenta,youyellow,koublack,wouwhite. C’est quand même assez explicite, il suffit d’écrire les noms en anglais. - Sous la forme d’un tuple correspondant aux valeurs RGB de la couleur. Cependant, ce tuple doit contenir des valeurs entre 0 et 1 (il suffit alors de diviser les valeurs RGB par
255.0). Ainsi, ce seracolor = (255 / 255.0, 0, 0)pour obtenir du rouge. Notons que nous pouvons ajouter une valeur (toujours entre 0 et 1) à ce tuple pour représenter la transparence alpha. - Sous la forme de chaîne de caractères représentant la couleur en notation hexadécimale. On aura donc
color = '#00FF00'pour obtenir du vert. - Et les adeptes des nuances de gris pourront donner en paramètre une chaîne de caractères correspondant à l’intensité en gris. Par exemple
color = '0.8'permet d’obtenir un gris pâle.
Nous avons donc plusieurs méthodes juste pour choisir une couleur.
Le style de ligne
Nous pouvons également changer le style des lignes en passant à la commande plot une chaîne de caractères. Les caractères acceptés et leur signification sont disponibles sur la documentation de la commande plot. Tous ces styles ne relient pas les points entre eux, certains ne font qu’afficher le signe à l’endroit où se situe le point. Présentons quelques caractères :
-est le style par défaut, il correspond à une ligne pleine ;--correspond à une ligne en pointillés ;:correspond à une ligne formée de points ;-.correspond à une ligne formée d’une suite de points et de tirets.
Ces caractères correspondent au paramètre linestyle. Nous pouvons aussi ajouter des marqueurs avec le paramètre marker qui rajoute alors un marqueur pour chaque point de votre graphique. Ce paramètre est aussi une chaîne de caractères. Voici quelques marqueurs : *, +, o.
Les chaînes de caractères représentant les marqueurs fonctionnent aussi avec le paramètre linestyle. Le contraire n’est pas vrai.
Nous pouvons également changer l’épaisseur du trait (ou des points) avec le paramètre lw (linewidth).
La grille
Nous pouvons ajouter une grille avec la fonction grid qui affiche un quadrillage en pointillés. Nous pouvons bien sûr changer le style de ce quadrillage.
- Le paramètre
axisnous permet de choisir quels axes doivent être quadrillés. Il peut prendre les valeursboth(les deux),xouy. - Le paramètre
colornous permet de choisir la couleur de l’axe. Il fonctionne de la même manière que le paramètrecolorde la fonctionplot. - Le paramètre
linewidthpermet de choisir l’épaisseur des traits. - Le paramètre
linestylepermet de choisir le style de quadrillage. Il peut prendre comme valeur (tout commeplot)-,--,:,-..
On a maintenant de quoi faire plusieurs styles de grilles.
Les axes
Nous pouvons effectuer plusieurs opérations sur les axes. Tout d’abord les légender :
xlabelpermet de donner un nom à l’axe des abscisses ;ylabelpermet de donner un nom à l’axe des ordonnées.
Ces deux commandes prennent en paramètres le nom que l’on veut donner à l’axe.
On peut également « cadrer » les axes avec la commande axis qu’on utilise ainsi : plt.axis([xmin, xmax, ymin, ymax]).
Une question d’échelle
Lorsque nous dessinerons des graphiques, nous aurons affaire à un problème particulier : la déformation.
Pour l’introduire, essayons de dessiner un carré centré autour de l’origine du repère. Traçons le carré ABCD avec A(1, 0), B(0, 1), C(-1, 0) et D(0, -1). Le code logique pour tracer ce carré est le suivant.
import matplotlib.pyplot as plt
x = [1, 0, -1, 0, 1]
y = [0, 1, 0, -1, 0]
plt.plot(x, y)
plt.show()
plt.close()
Pourtant, en exécutant ce code, on se rend compte que… Notre carré n’est pas carré.
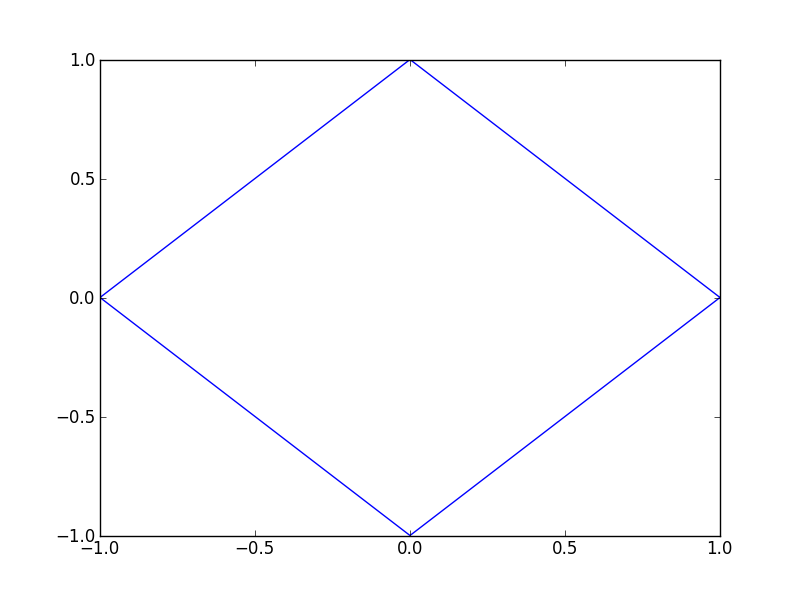
Cela est dû au fait que le repère choisi n’est pas orthonormal1. Pour rendre le repère orthonormal, nous pouvons utiliser la fonction axis en lui passant comme paramètre la chaîne de caractère 'equal'. Finalement, voici le code obtenu.
import matplotlib.pyplot as plt
x = [1, 0, -1, 0, 1]
y = [0, 1, 0, -1, 0]
plt.plot(x, y)
plt.axis('equal')
plt.show()
plt.close()
Et on obtient notre carré.
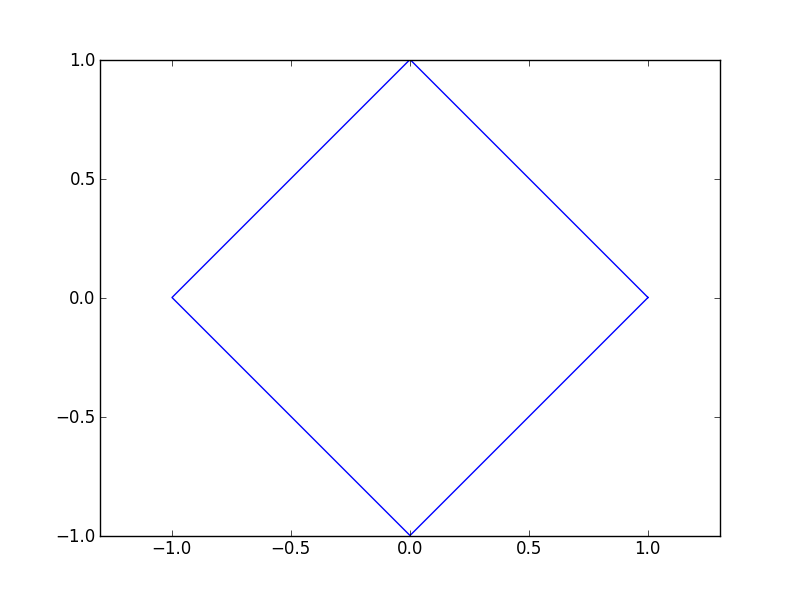
Voilà. C’est la fin de cette partie. Il nous faut maintenant pratiquer tout ce que nous avons vu, nous en aurons besoin pour la partie suivante.
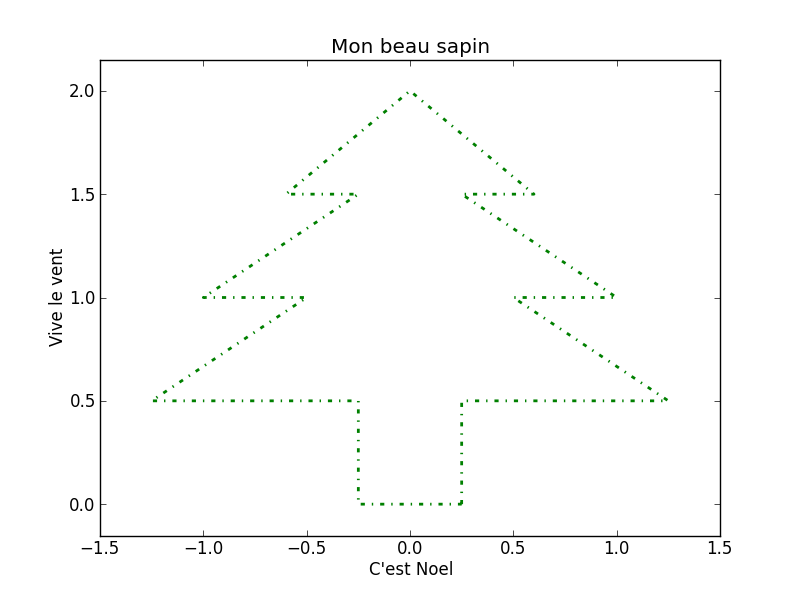
Voici un code qui utilise ce qu’on a vu pour afficher un beau sapin vert.
import matplotlib.pyplot as plt
x = [0.25, 0.25, 1.25, 0.5, 1, 0.25, 0.6, 0, -0.6, -0.25, -1, -0.5, -1.25, -0.25, -0.25, 0.25]
y = [0, 0.5, 0.5, 1, 1, 1.5, 1.5, 2, 1.5 , 1.5, 1, 1, 0.5, 0.5, 0, 0]
plt.plot(x, y, '-.', color = "green", lw = 2)
plt.title("Mon beau sapin")
plt.axis('equal')
plt.xlabel("C'est Noel")
plt.ylabel("Vive le vent")
plt.show()
plt.close()
- Un repère orthonormal (ou orthonormé) est un repère où tous les axes sont perpendiculaires entre eux et où l’unité est la même (il y a toujours la même distance entre le 0 et le 1).↩
Tracer des fonctions
Maintenant que nous avons vu comment utiliser le module pyplot, nous allons l’utiliser pour tracer des fonctions sur un intervalle donné.
La méthode secrète
Vous vous demandez sûrement comment nous allons faire pour tracer des fonctions. L’astuce est très simple. Nous allons relier des points dont nous savons qu’ils appartiennent à la courbe. Par exemple, pour tracer la fonction cosinus sur l’intervalle [0, 2π], nous allons relier les point A(0, cos(0)) et B(2π, cos(2π)).
Mais c’est nul ta méthode. On a essayé et on obtient juste une droite. Comment tu fais, toi, pour avoir une courbe ?
Oui, nous obtenons juste une droite, et c’est bien normal, nous avons juste relié deux points. Pour obtenir la courbe (en tout cas l’approcher), nous allons relier des points très proche qui appartiennent à la courbe. Par exemple, nous pouvons couper l’intervalle en 100 et donc relier 101 points plutôt que deux points. On appelle cela, subdiviser l’intervalle.
Notre subdivision sera à pas constant (le pas est l’espace entre deux points de la subdivision). Le pas est donc égal à la longueur de l’intervalle divisé par le nombre de points de la subdivision.
$$ \delta = \frac{x{max} - x{min}}{n}. $$
Ainsi pour dessiner la fonction cosinus :
- on coupe l’intervalle en tranches (on choisit par exemple ) ;
- le pas est donc ;
- on relie les points de la subdivision.
Nous pouvons remarquer qu’en divisant notre intervalle en 100 tranches, nous obtenons une subdivision de 101 points (les deux bornes de l’intervalle sont dans la subdivision).
Voici le code qui s’ensuit.
import matplotlib.pyplot as plt
from math import cos, pi
x = []
y = [] # On a créé deux listes vides pour contenir les abscisses et les ordonnées
pas = 2 * pi / 100
abscisse = 0 # L'abscisse de départ est 0
for k in range(0, 101): # On veut les points de 0 à 100
x.append(abscisse)
y.append(cos(abscisse)) # On rajoute l'abscisse et son image par la fonction cos aux listes
abscisse += pas # on augmente abscisse de pas pour passer au point suivant
plt.plot(x, y)
plt.show()
plt.close()
Là, nous obtenons une belle sinusoïdale.
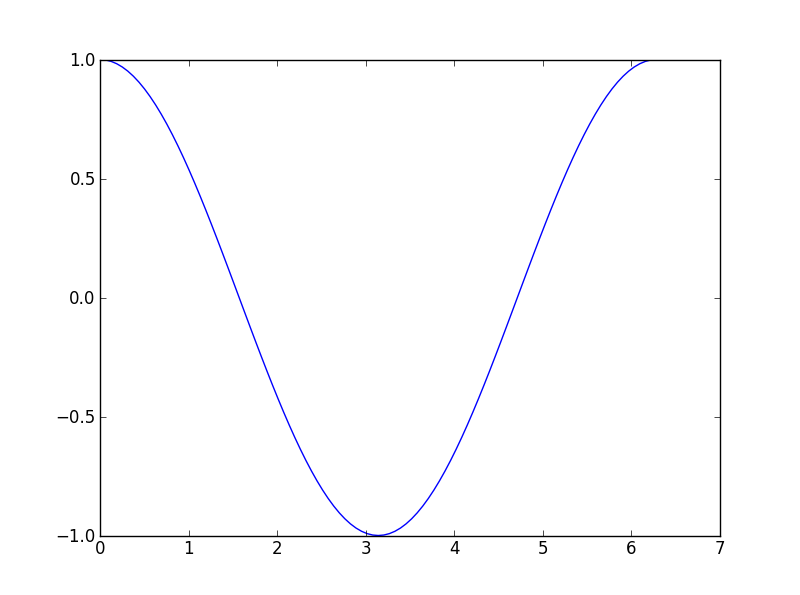
Maintenant, essayons de dessiner la fonction logarithme.
Voici la correction.
Afficher/Masquer le contenu masquéimport matplotlib.pyplot as plt
from math import log
a = 1
b = 20 # On choisit de dessiner sur [1, 20]
x = []
y = []
pas = (b - a) / 200 # On choisit de diviser l'intervalle en 200
abscisse = a # L'abscisse de départ est a cette fois
for k in range(0, 201): # On va donc de 0 à 200
x.append(abscisse)
y.append(log(abscisse))
abscisse += pas
plt.plot(x, y)
plt.show()
plt.close()
Les fonctions discontinues ou à valeurs interdites
Cependant, la méthode précédente peut présenter quelques problèmes dans des cas particuliers. Pour bien le voir, essayons de dessiner la fonction inverse () sur l’intervalle [-1, 1].
import matplotlib.pyplot as plt
a = -1
b = 1
x = []
y = []
pas = (b - a) / 200
abscisse = a
for k in range(0, 201):
x.append(abscisse)
y.append(1 / abscisse)
abscisse += pas
plt.axis([-1, 1, -10, 10])
plt.plot(x, y)
plt.show()
plt.close()
On obtient ce graphe.
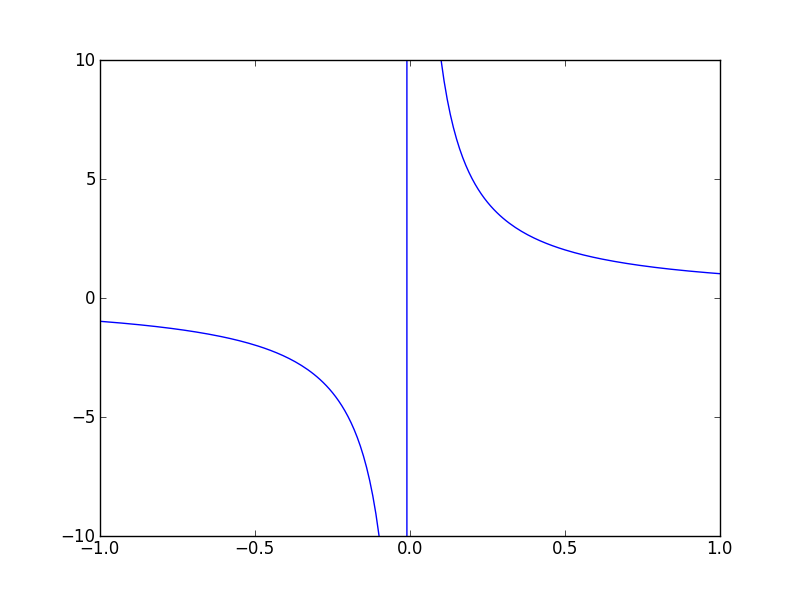
C’est quoi cette droite verticale au milieu de l’écran ?
La fonction inverse n’est pas définie en 0. Normalement, nous aurions dû obtenir une erreur lorsque nous demandions 1 / abscisse et qu’abscisse valait 0. Cependant, les erreurs d’approximation de python font que l’on ne passe pas par 0 mais par un point proche.
Néanmoins, il ne reste pas moins vrai que la fonction inverse est fortement divergente au voisinage de 0. Elle tend vers lorsque tend vers 0 par valeur négative mais tend au contraire vers lorsque tend vers 0 en étant positif.
La droite que nous observons est donc une conséquence de cela. On relie un point qui a une ordonnée très négative (le premier point avant 0) à un autre point qui a une ordonnée très positive (le premier point après 0).
Pour éviter cela, on est obligé de dessiner la fonction en deux fois. Une fois avant 0 et une fois après. Finalement, notre code est le suivant.
import matplotlib.pyplot as plt
a = 1 / 1000 # Pour éviter 0
b = 1
x = []
y = []
x1 = []
y1 = []
pas = (b - a) / 200
abscisse = a
for k in range(0, 201): # On fait une seule boucle
x.append(abscisse) # abscisse représente les abscisses à droite de 0
y.append(1 / abscisse)
x1.append(-abscisse) # -abscisse représente les abscisses à gauche de 0
y1.append(-1 / abscisse)
abscisse += pas
plt.axis([-1, 1, -10, 10])
plt.plot(x, y, x1, y1)
plt.show()
plt.close()
Et il nous donne bien cette courbe.
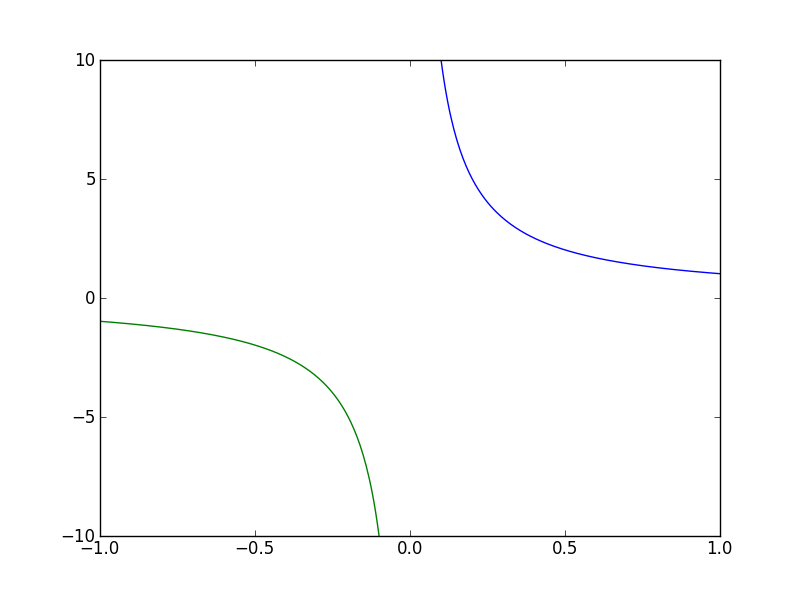
Nous pouvons bien entendu le modifier pour par exemple avoir les deux bouts de courbes de la même couleur, ou changer les axes.
Avec numpy (facultatif)
Pour ceux qui connaissent le module numpy1, sachez que plot accepte aussi ses modules, ce qui permet de faire ce que nous venons de faire plus simplement.
Pour la fonction cosinus, on peut alors écrire ce code.
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(0, 2 * np.pi, 0.01) # On crée un array qui va de 0 à 2pi exclu avec un pas de 0.01
plt.plot(x, np.cos(x)) # On utilise plot avec l'array x et l'array cos(x)
plt.show()
Et pour la fonction inverse celui-là.
import matplotlib.pyplot as plt
import numpy as np
def inverse(x): # Retourne l'array contenant les 1 / x
return np.array([1/i for i in x])
x = np.arange(0.01, 1, 0.01)
plt.plot(x, inverse(x), -x, inverse(-x))
plt.show()
- C’est le module de calcul numérique en Python.↩
Notre fonction
Nous avons maintenant tout pour faire notre fonction. Nous allons l’appeler zplot. Celle-ci ne devra pas ouvrir une fenêtre (donc pas de show) mais juste faire un plot. Ceci permettra de l’appeler deux fois par exemple pour dessiner la fonction inverse.
La fonction zplot minimale
Notre fonction zplot doit prendre comme paramètre :
- l’intervalle [a, b] sur lequel dessiner la fonction ;
- la fonction à dessiner ;
- il peut être intéressant de pouvoir choisir le pas.
Ainsi, notre prototype est le suivant.
def zplot(f, a, b, pas)
Maintenant, il ne reste plus qu’à faire ce que nous faisons depuis la partie précédente. Voici le code que nous finirons par obtenir.
import matplotlib.pyplot as plt
def zplot(f, a, b, n):
x = []
y = []
abscisse = a
pas = (b - a)/ n
for k in range(0, n + 1):
x.append(abscisse)
y.append(f(abscisse))
abscisse += pas
plt.plot(x, y)
Voilà. Avec cette fonction, il faut juste faire ceci pour avoir la courbe de la fonction cosinus sur [0, 2π] :
from math import cos, pi
zplot(cos, 0, 2 * pi, 100)
plt.show()
plt.close()
Oui d’accord, mais pour les fonctions qui ne sont pas définies, on fait comment ?
Là, nous avons deux possibilités :
- définir la fonction ;
- utiliser une fonction lambda.
Traçons la courbe de la fonction inverse sur l’intervalle [1, 10] des deux manières.
En définissant la fonction inverse, on obtient ce code.
def inverse(x):
return 1 / x
zplot(inverse, 1, 10, 200)
plt.show()
plt.close()
Et avec la fonction lambda, on obtient ce code.
zplot(lambda x : 1 / x, 1, 10, 200)
plt.show()
plt.close()
Nous le voyons, notre fonction zplot marche dans les deux situations.
Personnaliser zplot
Maintenant que nous avons fini notre fonction zplot, nous pouvons la personnaliser en ajoutant des paramètres (par exemple style pour le style de lignes et lw pour l’épaisseur du trait). Ces paramètres doivent être facultatifs pour ne pas avoir à les préciser à chaque fois (nous mettrons en paramètre par défaut les paramètres par défaut de plot). On obtient donc la fonction suivante.
def zplot(f, a, b, n, style = '-', lw = '1'):
x = []
y = []
abscisse = a
pas = (b - a)/ n
for k in range(0, n + 1):
x.append(abscisse)
y.append(f(abscisse))
abscisse += pas
plt.plot(x, y, style, lw = lw)
Et grâce à ça, nous pouvons par exemple tracer la fonction cosinus avec des étoiles.
from math import cos, pi
zplot(cos, 0, 2 * pi, 100, style = '*')
plt.show()
plt.close()
Et voilà le résultat.
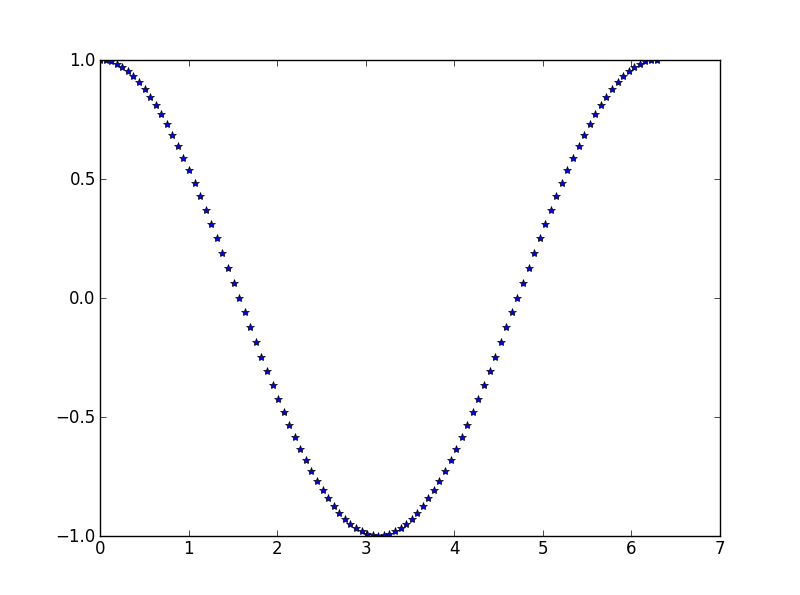
Notre fonction zplot pourrait être encore plus personnalisable. Nous pourrions afficher une grille par défaut, demander le nom de la courbe pour l’afficher en label, demander le nom des axes… Tout ça avec des nouveaux paramètres optionnels.
Voilà, c’est fini. Mais ce n’était qu’une introduction. Le module pyplot et surtout matplotlib peuvent faire beaucoup de choses.
Vous pouvez par exemple écrire sur les graphiques et les annoter avec les commandes text et annotate. Vous pouvez faire des histogrammes et même de la 3D avec matplotlib (si vous voulez tout savoir, même le logo de ce tutoriel est fait avec lui).
Allez vers la documentation pour en apprendre plus.
Vous pouvez également décider d’en apprendre plus sur numpy ou encore d’utiliser d’autres bibliothèques de dessin. La bibliothèque seaborn par exemple est basée sur matplotlib et permet de dessiner des graphiques (en particulier statistiques). Dans tous les cas, ne restez pas sur vos acquis, nous avons tous beaucoup plus à apprendre.
Mes remerciements à Gabbro et à Kje pour leurs commentaires durant la bêta. Je remercie également artragis pour son aide et ses commentaires durant la validation.