Que l’on conçoive directement des algorithmes ou que l’on utilise ceux à disposition dans les bibliothèques de nos langages, il advient toujours un moment où l’on se questionne sur l’efficacité d'un algorithme par rapport à un autre ou que l’on veuille prédire le temps d’exécution dans un contexte particulier.
Fort heureusement, la complexité algorithmique permet de répondre à cette question, et cette mesure est presque toujours mentionnée dans les documentations comme en atteste par exemple la recherche binaire de la bibliothèque C++, dont on nous renseigne qu’elle est en $\text{log}_2~(N)+2$, où $N$ est le nombre d’éléments du conteneur. Cela suffit-il cependant à comparer et prédire ? Rien n'est moins sûr comme nous allons le voir.
Cet écrit n’est pas à proprement parler un tutoriel ou un cours dans la mesure où il passe très vite sur les concepts abordés et ne vise pas à enseigner de manière à pouvoir « réutiliser » directement son contenu.
Il s’agit simplement d’apporter quelques réflexions et pistes de recherche pour le lecteur curieux sur ce qu’est la complexité des algorithmes, les différentes mesures qui existent et une partie de l’état de l’art de la recherche sur le sujet.
Pour ces raisons, il est possible que beaucoup de termes ne soient pas familiers au lecteur, ce qui ne doit pas le décourager mais plutôt éveiller suffisamment sa curiosité pour se renseigner sur les différents concepts dont il est question.
C’est un choix pédagogique qui fait que cet écrit est plus proche d'un article que d’un tutoriel. Cependant, sa longueur et la multitude des champs techniques abordés n’en font pas un bon candidat pour être un article au format de Zeste de Savoir.
- Avant-propos
- Position du problème
- Mesures de complexité d’un algorithme
- Vers des critères de difficulté en amont
- Robustesse théorique et empirique d’un algorithme
Avant-propos
La complexité algorithmique est l’étude du lien, souvent temporel, mais aussi spatial1, entre un problème et un algorithme particulier. Puis en élargissant, l’étude d’un problème par rapport à l’ensemble des algorithmes connus qui le résolvent.
Il s’agit donc de caractériser la difficulté d’un problème au travers des méthodes de résolution.
Une seconde approche plus récente, en tout cas dans ses résultats les plus novateurs, consiste à essayer d’établir la difficulté du problème par rapport à ses caractéristiques intrinsèques. Pour cela, il est évident qu’il faut pouvoir trouver un langage commun d’expression des problèmes, et ce langage est la mathématique et plus précisément la programmation mathématique, un domaine de la recherche opérationnelle.
Le terme « programmation » n’a ici rien à voir avec l’informatique, mais doit son origine, tout comme le terme « recherche opérationnelle » au vocabulaire militaire puisque la discipline est née durant la seconde guerre mondiale, notamment pour l’élaboration du plan optimal de gestion de certaines ressources, c’est-à-dire la recherche de la meilleure façon d’opérer. En cela, la programmation mathématique est en réalité ramenée à de l’optimisation.
Dans cet article nous tâcherons de montrer qu’une très vaste partie des problèmes peut se poser sous la forme d’un problème d’optimisation, notamment au travers ici de l’exemple de l’optimisation linéaire. Par la suite nous expliquerons en quoi les études de complexité n’arrivent plus à caractériser pleinement la difficulté d’un problème, notamment au travers de l’évolution des attentes des performances des algorithmes, ainsi que des facteurs influençant la qualité empirique des algorithmes. Fort de ce constat, nous expliciterons quelques propriétés en amont, c’est-à-dire du point de vue du problème, qui caractérisent un problème difficile, et donc sans disposer explicitement de méthode de résolution. Enfin, nous donnerons quelques pistes supplémentaires pour faire le lien avec des propriétés des algorithmes, notamment leur robustesse et leur paramétrisation.
L’enjeu ici est de montrer les difficultés à caractériser les performances d’un algorithme et donc à fortiori, la difficulté d’un problème par rapport aux algorithmes qui le résolvent.
-
c'est à dire la quantité de mémoire nécessaire pour résoudre le problème avec l'algorithme ↩
Position du problème
Le problème d’optimisation linéaire
Définissons le problème
Commençons par un petit rappel :
Définition : Une fonction $f$ est linéaire si elle satisfait le principe de superposition, c’est-à-dire si $\forall x,y,\alpha \in \mathbb{R}^3,~ f(x+\alpha y) = f(x) + \alpha f(y)$.
Le problème d’optimisation linéaire est un problème qui vise à minimiser (ou maximiser) une fonction linéaire $f$ tout en respectant des contraintes elles aussi linéaires. Concrètement, $f$ est une combinaison linéaire d’un certain nombre $n$ de variables et peut donc s’écrire $c^{\top }x$, avec $c\in \mathbb{R}^n$ et $x\in \mathbb{R}^n$. Les $n$ variables dites de décisions, sont alors soumises à $m$ contraintes, de la forme $a_i^{\top} x \leq b_i, \forall 1 \leq i \leq m$, avec $a_i \in \mathbb{R}^n$ et $b_i \in \mathbb{R}$.
Pour plus de concision, on peut écrire cette formulation sous forme matricielle :
Avec $A \in \mathbb{M}^{m \times n}(\mathbb{R})$ et $b \in \mathbb{R}^m$.
Un exemple concret : planifier une production
Un exemple « concret » de situation que ce genre de modèle capture serait le suivant. Nous sommes à la tête d’une armée, en guerre contre une nation. Nous prévoyons de produire 20 avions divisés en deux modèles. Selon le modèle, un avion est armé de $b_j$ bombes et $m_j$ missiles et il cause des dégâts estimés par $c_j$. On résume tout cela dans le tableau suivant :
| modèle A | modèle B | |
|---|---|---|
| bombes | 3 | 15 |
| missiles | 5 | 10 |
| dégâts | 5 | 11 |
On dispose au total de 225 bombes et 160 missiles. La question est la suivante : combien d’avions de chaque modèle doit-on produire pour maximiser les dégâts infligés à l’ennemi ?
Modélisons cela par un programme d’optimisation linéaire
Et voici la modélisation mathématique pour se ramener au problème d’optimisation linéaire. On appelle $x_A$ et $x_B$ les quantités d’avions à produire, respectivement du modèle A et du modèle B. Les dégâts totaux peuvent s’écrire comme $5x_A + 11x_B$, et l’on cherche donc à maximiser $f(x_A, x_B) = 5x_A + 11x_B$. La première contrainte est évidemment l’ensemble des 20 avions que l’on peut produire. Ainsi $x_A + x_B \leq 20$. De même, nous disposons de contraintes sur le nombre total de bombes et de missiles ce qui conduit à deux contraintes supplémentaires : $3x_A + 15x_B \leq 225$ et $5x_A + 10x_B \leq 160$. Enfin, il faut rajouter des contraintes logiques : les quantités d’avions à produire ne peuvent être que positives et donc $x_A$ et $x_B$ sont positifs.
Matriciellement, nous aurions $c = \begin{pmatrix}5 \\11\end{pmatrix}$, $A = \begin{pmatrix}1 & 1 \\ 3 & 15 \\5 & 10 \end{pmatrix}$ et $b = \begin{pmatrix}20 \\ 225 \\ 160 \end{pmatrix}$.
Visualisons notre problème
Comme nous n’avons que deux variables de décision, il est possible de visualiser les contraintes comme montré sur la figure suivante. Chaque contrainte est représentée par une droite limitant les valeurs possibles pour $x_A$ et $x_B$. Par exemple, si l’on prend la première contrainte, en vert sur la figure, tout point dans la zone verte, sous la droite, est un point qui satisfait cette contrainte. Le domaine, dit admissible, des points satisfaisant toutes les contraintes à la fois est obtenu par l’intersection des domaines admissibles pour chaque contrainte prise individuellement. Il se peut donc que le domaine soit non borné, réduit à un point, voire vide, dans le cas où les contraintes sont antinomiques.
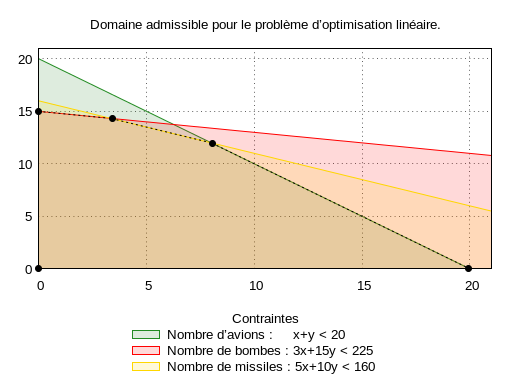
En l’occurrence, il est défini par le polyèdre délimité par les points noirs. Chaque point à l’intérieur de ce domaine satisfait toutes les contraintes et l’objectif du problème est donc de trouver le point qui maximise notre fonction de départ. Par exemple, en prenant le point $(5,5)$, on obtient $f(5,5) = 80$ et l’on voit que l’on peut largement faire mieux avec $(7,7)$ qui donne $f(7,7) = 112$. Sans plus d’explications, la solution optimale est donnée par $(4,14)$ pour des dégâts de $174$. Notons au passage que pour faire un maximum de dégâts, il ne nous faut pas construire 20 avions mais seulement 18.
Quelques pistes pour résoudre et lien avec la complexité
Il existe plusieurs méthodes pour la résolution du problème d’optimisation linéaire et si nous renvoyons le lecteur à la littérature sur le sujet pour de plus amples détails, nous nous contenterons de les citer pour l’intérêt qu’elles présentent en terme de complexité.
Proposée par Dantzig en 1947, la méthode du Simplexe est un algorithme qui possède une complexité dans le pire des cas qui est exponentielle, mais dont les performances empiriques sont excellentes, au point qu’il s’agit encore aujourd’hui d’une méthode très utilisée. À contrario, la méthode des points intérieurs proposée par Khachiyan en 1979 exhibe une complexité dans le pire des cas qui est polynomiale mais s’avère pourtant inefficace en pratique et la méthode du Simplexe est plus rapide sur l’immense majorité des instances. Enfin, Karmarkar propose en 1984 une variante de la méthode des points intérieurs qui est à la fois efficace théoriquement et en pratique.
On va tenter d’expliquer les raisons qui font que l’on puisse obtenir de telles inconsistances entre les prédictions théoriques de la complexité (dans le pire des cas) et les résultats en pratique. Il s’agit notamment de rétablir ce qu’est exactement un comportement asymptotique, par rapport à ce qu’on essaye de lui faire dire habituellement, puis de présenter les différentes mesures de complexité qui existent et dont la création résulte de la volonté de combler les lacunes de la mesure précédente.
Quelques notations et remarques de vocabulaire
Pour un problème $P$, on note $\Pi$ l’ensemble des instances possibles.
On note $\Pi_n$ l’ensemble des instances d’un problème dont la taille d’écriture est $n$.
Le nombre d’opérations nécessaires à la résolution de l’instance $\pi$ par l’algorithme $A$ est noté $T_A(\pi)$.
Problème d’ordre total pour la comparaison d’algorithmes
Nous nous donnons deux algorithmes, $A$ et $B$, pour résoudre un problème $P$ dont l’ensemble des instances est $\Pi$. Dans le cas où $\Pi$ ne contient qu’une instance $\pi$, on peut comparer simplement les algorithmes $A$ et $B$ sur le problème $P$ en observant le comportement sur $\pi$ : si $T_A(\pi) \leq T_B(\pi)$ alors $A \underset{P}{\succ} B$, c’est-à-dire que $A$ est meilleur que $B$ pour la résolution du problème $P$.
Dès lors que l’on introduit une seconde instance $\pi’ \in \Pi$, les choses deviennent moins évidentes. En effet, il se peut que $T_A(\pi) \leq T_B(\pi)$ et $T_A(\pi’) \geq T_B(\pi’)$, autrement dit que $A$ soit meilleur que $B$ pour l’instance $\pi$ mais moins bon pour $\pi’$.
Ainsi, il est impossible a priori d’obtenir une relation d’ordre totale sur les algorithmes $A$ et $B$ au regard du problème $P$. Il est évident que plus l’ensemble des instances est large et plus la probabilité de pouvoir établir une telle relation tend vers 0.
Il faut malgré tout trouver une mesure d’efficacité pour les algorithmes afin de pouvoir les comparer. Une mesure qui s’est imposée est la mesure asymptotique en fonction de la taille du problème. Comme nous allons le voir, cela n’est pas sans poser quelques problèmes de première importance.
Mesures de complexité d’un algorithme
Remarques préliminaires
On définit la complexité d’un problème comme la complexité minimale d’un algorithme permettant de résoudre toutes les instances de ce problème1. Cependant, en disant cela, non seulement on manque de précision en omettant que nous prenons pour référence la complexité dans le pire des cas, mais en plus, on fait naître un tas de questions auxquelles cet indicateur uni-dimensionnel ne peut vraisemblablement répondre.
En effet, quelle est la répartition des instances par rapport à leur difficulté ? Quelle est la sensibilité de mon algorithme par rapport à la perturbation des instances ? Quelle est l’efficacité pratique de mon algorithme ? Pour répondre à ces questions, plusieurs mesures de la complexité algorithmique ont été développées.
Pire des cas
La mesure la plus fréquente est la mesure dans le pire des cas. Il s’agit de donner une borne supérieure du nombre d’étapes nécessaires à la terminaison de l’algorithme sur l’ensemble des instances du problème qu’il résout. De manière formelle, la complexité d’un algorithme dans le pire des cas est défini par : $T_{\text{max}}(n) = \underset{\pi \in \Pi_n }{\text{max}}~T(\pi)$.
Il peut être difficile de trouver la valeur exacte en fonction de $n$, et l’on utilise souvent la notation de Landeau $\mathcal{O}$ pour exprimer l’ordre de grandeur. Dire que l’algorithme $\mathcal{A}$ a une complexité dans le pire des cas de $\mathcal{O}(n^2)$ veut dire $\exists a \in \mathbb{N}, ~\forall \pi \in \Pi_n,~ T(\pi) \leq a \times n^2$.
Il faut comprendre que si $T_{\max}(.)$ est le nombre exact du nombre d’opérations effectuées dans le pire des cas, $\mathcal{O}(.)$ ne représente qu’une approximation dont la précision grandit avec la taille du problème : on parle d’estimation asymptotique.
Meilleur des cas
La mesure de la complexité dans le meilleur des cas se définit symétriquement par rapport à la notion dans le pire des cas : $T_{\text{min}}(n) = \underset{\pi \in \Pi_n}{min} ~ T(\pi)$, c’est-à-dire comme le minimum du nombre d’étapes pour résoudre une instance parmi toutes les instances.
De fait, nous obtenons un encadrement sur le nombre d’opérations nécessaires à la résolution d’un problème, c’est-à-dire indépendamment de l’instance choisie :
Étude de l’encadrement sur exemple
Imaginons que l’on dispose de trois algorithmes dont on a calculé la complexité dans le pire et le meilleur des cas et que l’on peut résumer par le tableau suivant :
| Algorithme | Meilleur des cas | Pire des cas |
|---|---|---|
| A | $f_{\text{min}}(n)=n^2$ | $f_{\text{max}}(n)=n^2 \times \frac{log(n)}{2}$ |
| B | $g_{\text{min}}(n)=0$ | $g_{\text{max}}(n)=n^2 + 2000 \times abs(cos(n))$ |
| C | $h_{\text{min}}(n)=5000$ | $h_{\text{max}}(n)=n^{\frac 6 5} \times log(x^5 + 2x^3 + 7x^2) + 5000$ |
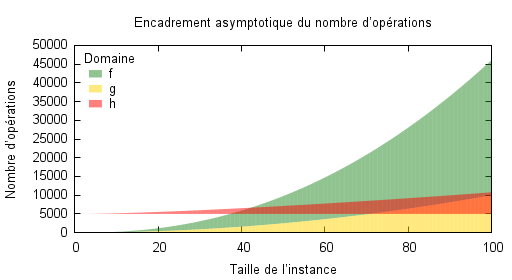
Sur la figure qui suit, on peut observer le domaine du nombre d’opérations pour chacun des trois algorithmes. Quelle que soit l’instance considérée, le nombre d’opérations sera toujours dans la zone colorée. Remarquons par exemple que l’algorithme $A$ possède un nombre minimal d’opérations qui dépend de la taille de l’instance tandis que l’algorithme $C$ possède un coût minimal fixe de $5000$, qui correspond certainement à un pré-traitement indépendant de la taille de l’instance. Enfin, l’algorithme $B$ possède un comportement oscillant pour sa borne supérieure, malgré une tendance croissante. Si cette oscillation n’a que peu d’importance au fur et à mesure que les instances grandissent, elle peut cependant être importante pour des instances de petite taille.
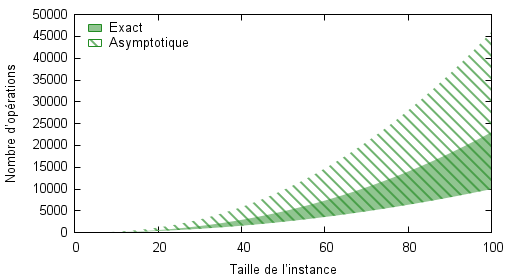
Voyons maintenant les différences qu’il peut exister entre la complexité exacte et la complexité asymptotique. Les cinq images suivantes montrent le tracé de la complexité exacte et asymptotique en fonction de la taille des instances. Dans le cas de l’algorithme C, on dispose également de deux plages différentes de taille d’instances, ce qui nous permettra de visualiser certains défauts de la complexité asymptotique pour l’évaluation pratique de la performance des algorithmes.
Pour l’algorithme A, on constate sur la figure suivante que l’estimation asymptotique est une borne supérieure au nombre d’opérations, et ce, quel que soit la plage de valeurs de la taille des instances considérées.
À contrario, dans le cas de l’algorithme $B$ l’ordre de grandeur asymptotique (OGA, sigle propre à cet article) de la complexité exacte est toujours majoré par la valeur exacte. Cependant, on pressent que pour de grandes valeurs de $n$, cela est moins problématique, comme on le vérifiera par la suite.

Le cas de l’algorithme $C$ est intéressant puisque le coût constant n’apparaît évidemment pas dans l’OGA et de ce fait, pour de petites valeurs de $n$, l’OGA décrit un comportement qu’il n’est pas possible d’obtenir. Il est en effet impossible d’obtenir une instance de taille 40 qui ne nécessite que 500 opérations par exemple. On tombe ensuite exactement dans le cas de figure de l’algorithme $B$, les oscillations en moins, c’est-à-dire que l’OGA sous-estime toujours la valeur exacte mais qu’à terme, cette différence est négligeable dans le nombre total exact d’opérations.

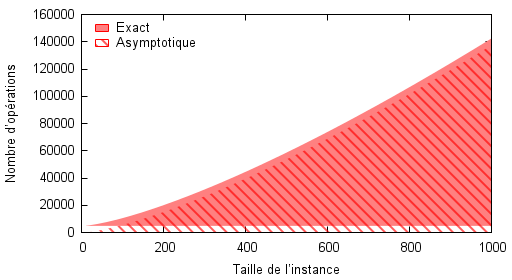
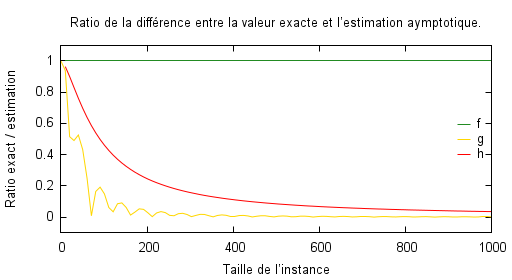
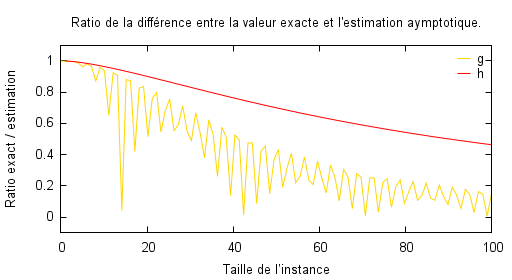
C’est ce que l’on peut observer sur les deux figures qui suivent et qui représentent l’écart relatif entre le nombre d’opérations exact et son OGA. Il y a plusieurs remarques à faire :
-
Les algorithmes $B$ et $C$ présentent une convergence vers $0$ lorsque la taille $n$ tend vers l’infini. Ceci permet de relativiser le fait que l’OGA donne sur ces deux cas une valeur inférieure au nombre exact. Ceci permet de mettre en évidence la définition même de la complexité asymptotique : le nombre d’opérations de l’algorithme va se comporter comme son OGA au voisinage de l’infini, où l’infini est en pratique une notion qui dépend de l’algorithme et de l’utilisateur (c’est-à-dire de l’utilisation qu’il fait de l’algorithme et ce qu’il en attend). On remarque ainsi qu’on peut raisonnablement considérer que l’algorithme $B$ se comporte comme son OGA pour une taille environ égale à 400 tandis que pour l’algorithme $C$, il faut attendre plus longtemps.
Et voici où la complexité asymptotique échoue : en supposant que l’utilisateur de l’algorithme $B$ ou $C$ ne va avoir à traiter en pratique que des instances de taille comprise entre 0 et 100, alors on peut voir que l’algorithme est très loin de se comporter comme le prédit la complexité asymptotique. C’est d’autant plus visible sur l’algorithme $B$ dont les oscillations sont prépondérantes pour ces valeurs. Or, à partir du moment où l’on n’indique pas les tailles pour lesquelles les algorithmes vont avoir une complexité qui va se comporter comme leur OGA, la prédiction d’un algorithme sur un jeu d’instances peut être largement faussée, tout comme la comparaison entre deux algorithmes à priori. -
L’importance de la constante multiplicative du terme prépondérant, c’est-à-dire celle de l’OGA, est totalement passée sous silence. Or, on voit très bien que dans le cas de l’algorithme $A$, l’écart entre la valeur donnée par l’asymptote et la valeur exacte ne va jamais tendre vers 0. Dans ce cas précis, l’OGA indique un nombre d’opérations deux fois supérieur au nombre exact et il ne s’agit pourtant que d’un petit facteur $\frac 1 2$. On peut imaginer à quel point les prédictions sont faussées par des constantes énormes qui peuvent apparaitre dans le calcul exact mais pas dans l’OGA, avec pour effet de rendre la comparaison d’algorithmes impossible à priori comme nous le verrons par la suite.
Complexité en moyenne
Vers la complexité en moyenne
L’encadrement donné plus haut atteint ses limites assez rapidement. Dans bien des problèmes un peu complexes, il est possible que notre algorithme ne soit pas capable de traiter un ensemble d’instances particulières ou que sa complexité dans le pire des cas soit telle qu’on puisse la considérer comme infinie même pour des instances de petite taille.
Malgré tout, on remarque très souvent qu’en pratique ces cas pathologiques n’arrivent que rarement si ce n’est jamais, et l’on peut munir l’espace $\Pi$ d’une distribution de probabilité, décrivant la probabilité d’apparition d’une instance à traiter en pratique. On appelle par la suite, par commodité, l’ensemble des instances dont la probabilité d’apparition est strictement supérieure à 0 le « sous-ensemble des instances pratiques ».
Le sous-ensemble des instances pratiques dépend de la configuration de l’exploitation de l’algorithme. C’est-à-dire que d’une part pour un même algorithme utilisé par une entreprise A et une entreprise B, la plage de la taille possible des instances peut varier, et d’autre part, de par leurs activités différentes elles peuvent ne pas avoir les mêmes cas à traiter en règle générale.
Prenons un exemple concret, avec Amazon et un petit libraire qui utilisent tous deux le même algorithme de tournée de véhicules afin de déterminer le plan pour les livraisons de leurs livres. Évidemment le libraire ne livre que dans son quartier et a moins de commandes à traiter qu’Amazon. De fait, si le domaine théorique pour le nombre de clients à livrer est $\mathbb{N}$, en pratique il sera probablement $[a_1,a_2] \subset \mathbb{N}$ pour Amazon et $[b_1,b_2] \subset \mathbb{N}$ pour le libraire, avec à priori $b_2 < a_2$, pour traduire le fait qu’Amazon peut recevoir bien plus de commandes. Mais ce n’est pas tout ! Avec ces mêmes considérations sur le nombre de clients, il est probable que le nombre de commandes du libraire soit bien plus variable au sein de sa plage que celui d’Amazon, par la force de la loi des grands nombres. Ainsi, pour Amazon, la distribution du nombre de clients par jour suivra peut-être quelque chose qui ressemble à une loi normale, centrée sur $\frac{a_1+a_2}{2}$, tandis que dans le cas du libraire il se pourrait que le nombre de clients se modélise plutôt par une loi uniforme sur $[b_1,b_2]$. Encore plus problématique, pour une même taille de problème, la configuration géographique des clients pourrait grandement influer sur le nombre d’opérations nécessaires à l’algorithme pour trouver la solution.
La complexité dans le meilleur et le pire des cas ne permettent pas de capter ces notions. C’est pourquoi d’autres approches, comme la complexité en moyenne, la complexité amortie ou la complexité lisse, tentent de combler ces lacunes.
Partant du principe que les instances pathologiques sont souvent exclues du sous-ensemble des instances pratiques ou suffisamment rares en son sein pour ne pas être considérées comme significatives, on s’intéresse à la complexité en moyenne d’un algorithme. Par cette approche on essaye de déterminer le comportement normal ou attendu d’un algorithme. Mais contrairement à l’idée reçue, il ne s’agit pas de simplement faire une moyenne du nombre d’opérations nécessaires à la résolution de chaque instance possible – ceci étant un cas particulier et par ailleurs plus proche de la complexité amortie –, mais d’émettre une hypothèse sur la distribution de probabilité d’apparition des instances possibles. Il s’agit donc avant toute chose d’une mesure vis-à-vis d’une situation d’exploitation plus ou moins concrète puisqu’elle présuppose de répondre en amont à la question de la distribution des instances.
Présentation et discussion de la complexité en moyenne
Supposons une mesure de probabilité $\mu$ sur l’ensemble des instances $\Pi$ . Alors la complexité moyenne est definie par $\bar T(\Pi) = E_\mu[T(\Pi)]$, c’est-à-dire l’espérance par rapport à cette mesure.
Dans le cas où $\Pi$ est un ensemble discret, on a $\bar T(\Pi) = E_\mu[T(\Pi)] = \underset{{\pi \in \Pi} }{\sum}\mu(\pi) T(\pi)$, et pour $\Pi$ continu $\bar T(\Pi) = E_\mu[T(\Pi)] = \int_{\Pi} T(\pi) \mu(d\pi)$.
Remarquez que contrairement à la complexité dans le pire ou le meilleur des cas, les instances considérées ne sont pas nécessairement de la même taille. En pratique, le calcul exact de la complexité en moyenne est extrêmement difficile si ce n’est impossible car il suppose que l’on puisse obtenir le nombre exact d’opérations nécessaires à la résolution de chacune des instances de l’ensemble $\Pi$.
En plus de cela, le calcul exact perd tout intérêt en sachant que la mesure de probabilité $\mu$ n’est jamais connue en pratique, si ce n’est pour des exemples artificiels. Par exemple si l’on génère de manière aléatoire des tableaux à trier de même taille, où chaque case sera remplie selon une même loi uniforme, alors toutes les instances auront même probabilité et l’on retrouvera un calcul de moyenne arithmétique habituelle (le cas particulier évoqué plus haut).
Comme le calcul exact est rendu impossible, on préférera une approche empirique : on mesure les performances moyennes de l’algorithme en phase d’exploitation, par exemple au niveau d’Amazon ou de notre petit libraire. Les résultats seront bien différents et le désavantage sera de ne pouvoir tirer de conclusion générale sur la difficulté du problème en tant que tel ou bien sur les capacités globales de l’algorithme sur le problème donné.
Cela rajoute un élément à l’objet dont on cherche à caractériser la difficulté. En effet, auparavant on avait la simple composante $(\text{algorithme})$ et maintenant nous avons le couple $(\text{algorithme}, \text{utilisateur})$. Évidemment on pourrait faire une moyenne pour chacun des utilisateurs pour se ramener à une complexité moyenne de l’algorithme. C’est bien sûr impossible logistiquement parlant mais également pas tout à fait souhaitable à bien des égards, notamment parce que l’on cherche plutôt une caractérisation à priori de la difficulté d’un problème et non pas à postériori par l’efficacité pratique d’un algorithme.
Une remarque importante à faire est que pour l’évaluation empirique, on préférera utiliser la valeur médiane du nombre d’opérations car elle est moins sensible aux valeurs extrêmes. Pour compléter, l’étude de la différence entre la valeur médiane et la moyenne permet de confirmer ou d’infirmer l’hypothèse selon laquelle les instances difficiles apparaissent peu souvent. En réalité, un histogramme serait la solution la plus complète car il permet d’observer la distribution de la difficulté des instances et de mettre en place des tests statistiques pour valider notre hypothèse initiale sur la distribution.
Analyse amortie
L’idée principale de l’analyse amortie est de considérer que certaines opérations coûteuses apportent un bénéfice à l’ensemble du flux d’instructions qui suit, amortissant ce (sur)coût.
L’exemple le plus simple serait la politique d’allocation d’un tableau dynamique. Celui-ci est constitué d’une capacité mémoire $c$, contiguë, et d’une taille $t$, qui est le nombre d’éléments présents dans le tableau. Lorsque l’on ajoute un élément il peut se passer deux cas :
- $t < c$ : il reste donc de la place en mémoire et on peut ajouter l’élément en temps constant, c’est-à-dire asymptotiquement en $\mathcal{O}(1)$.
- $t = c$ : et donc il n’y a pas assez de place pour rajouter l’élément. Comme il faut conserver la propriété de continuité en mémoire, une nouvelle zone mémoire est allouée, plus grande, et les éléments déjà présents sont copiés de l’ancien emplacement au nouveau, puis le nouvel élément est inséré, ce qui se fait cette fois en $\mathcal{O}(t)$.
L’exemple du tableau dynamique
Quelle est la complexité dans le pire des cas de l’opération d’insertion pour un tableau dynamique ? La réponse est $\mathcal{O}(t)$ en considérant que l’on démarre avec une capacité de 0 et que l’on n’agrandit le tableau que d’une unité à chaque fois. Mais d’une part, on peut retarder le besoin d’une nouvelle allocation en initialisant notre tableau avec une capacité qui est la taille estimée nécessaire pour notre application ; et d’autre part, on peut se dire que dans tous les cas, n’augmenter la capacité que d’une unité n’est pas un bon pari pour l’avenir. Le travail de l’analyse amortie est donc de prendre en compte le fait que certaines opérations coûteuses permettent l’existence de multiples opérations non-coûteuses et que donc, dans la complexité, on peut « répartir » le coût de ces lourdes opérations sur toutes les opérations élémentaires engendrées.
Pour définir la complexité amortie, il faut définir le coût amorti de chaque opération, lors d'une série de $n$ opérations : $T_{\text{amo}}(n) = \frac{T_{\text{max}}(n)}{n}$ 2.
Dans le cas du tableau dynamique, on remarque que pour insérer $n$ valeurs dans un tableau de taille $n$, cela prend pour chaque opération un temps constant, sauf pour la dernière qui déclenche une réallocation en $\mathcal{O}(n)$. Ainsi, la complexité amortie pour l’insertion est donnée par $T_{\text{amo}}(n) = \frac{\mathcal{O}(n)}{n} = \mathcal{O}(1)$.
Les trois figures suivantes illustrent le nombre nécessaire d’opérations pour une série allant de 1 à 10 insertions en partant d’un tableau vide, avec l’évolution de la capacité disponible. La première politique consiste à simplement incrémenter la capacité lorsque cela est nécessaire, autrement dit à chaque insertion. La seconde politique se donne un peu plus de marge en ajoutant trois à la capacité. Enfin la dernière multiplie la taille de la capacité par deux chaque fois que cela est nécessaire. On a donc une progression exponentielle de la capacité dans ce cas.
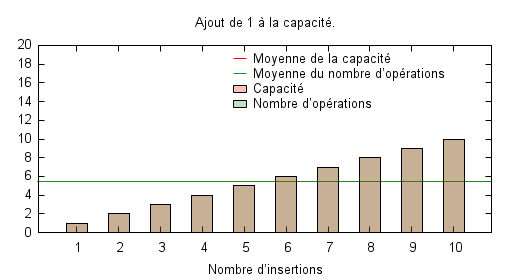
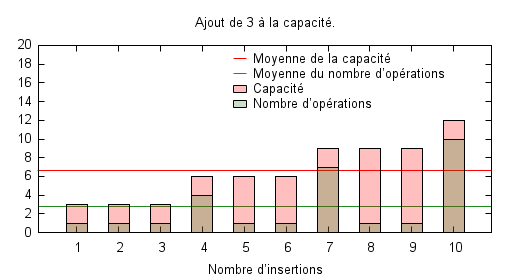
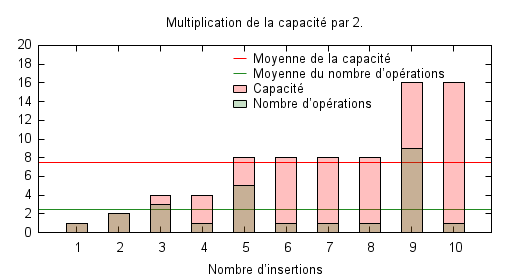
Il est évident que la première politique est optimale en terme de capacité : aucun espace mémoire n’est jamais inutilisé. Par contre, elle possède un coût moyen important qui est même le pire des cas possibles. Rien que le fait d’ajouter trois unités au lieu d’une seule permet de faire tomber sensiblement le coût moyen de la série d’insertions à 2,8 mais augmente de facto la capacité moyenne, laquelle passe de 5,5 à 6,6. Enfin, la politique exponentielle permet de diminuer encore un peu le nombre moyen d’opération à 2,5 tout en augmenter légèrement la capacité moyenne.
En réalité, si l’on refaisait le tracé sur une série d’insertions plus longue, on s’apercevrait que les politiques additives sont peu scalables par rapport aux politiques exponentielles, c’est à dire qu’elles sont mal adaptées au changement d’ordre de grandeur de la taille des tableaux utilisés. Ceci explique qu’en pratique on n’utilise que ces dernières, puisqu’elles permettent un meilleur compromis entre la capacité inutilisée et le nombre moyen d’opérations à effectuer.
Discussion sur l’analyse amortie
Bien souvent, l’amélioration de l’analyse amortie se fait par des heuristiques qui font augmenter la complexité dans le pire des cas ou d’autres caractéristiques comme la complexité spatiale (par exemple, dans le cas du tableau dynamique, on a en pratique en permanence une occupation mémoire qui n’est pas nécessaire). Il est aussi possible que ces heuristiques rendent difficile l’étude de la complexité dans le pire des cas. Cependant, leur but est d’apporter plus de robustesse à l’algorithme, qui réagira mieux en limitant l’impact des opérations coûteuses sur la grande majorité des instances. Le réglage de ces heuristiques est un choix souvent lié à un compromis comme nous l’avons vu sur l’exemple précédent, et l’on abordera très rapidement cette question à la fin de cet article. Notons simplement que dans les cas simples comme celui d’un tableau dynamique, le choix exact des paramètres n’a guère d’influence et c’est ainsi qu’on conseille théoriquement de doubler la taille du tableau à chaque réallocation, mais que les listes en Python utilisent un facteur $\frac{9}{8}$3 par exemple.
L’exemple spectaculaire d’Union-Find
Il me semble important de présenter l’une des applications les plus spectaculaires de la complexité amortie, à savoir le cas de la structure de données Union-Find, utilisée entre autre dans l’algorithme de Kruskal pour la recherche d’arbre couvrant de poids minimal.
Union-Find est une structure de données utile pour maintenir une partition d’un ensemble en classes disjointes. Elle possède deux opérations :
- Find, qui détermine la classe à laquelle appartient d’un élément en renvoyant son « représentant » ;
- Union, qui fusionne deux classes en une seule.
Sans plus d’informations, l’implémentation peut se faire via l’utilisation de différentes structures de données sous-jacentes, mais va alors entrainer des complexités différentes. C’est ainsi qu’une implémentation triviale utilisant des listes chaînées pour la représentation des classes aura une complexité amortie en $\mathcal{O}(m+n\;\text{log}~n)$ lorsque l’on effectue $m$ appels successifs à Union puis Find sur $n$ éléments.
Une solution est alors d’utiliser des arbres qui, combinés à une heuristique dite du rang, permettent de faire tomber la complexité amortie à $\mathcal{O}(\text{log}~n)$. L’utilisation d’une seconde heuristique, la compression de chemin, permet de faire tomber la complexité en… $\mathcal{O}(\alpha(n))$ où $\alpha$ est l’inverse de la fonction d’Ackermann.
La fonction d’Ackermann est une fonction qui croit tellement vite que l’on peut considérer que son inverse est inférieure ou égale à quatre quelle que soit la valeur de $n$. En effet, la fonction d’Ackermann en $4$ est de l’ordre de $10^{80}$, autrement dit l’ordre de grandeur du nombre d’atomes dans l’univers ! Et si l’on renvoie le lecteur à la littérature pour plus de renseignements sur Union-Find et la démonstration de la complexité amortie associée, l’exemple est donné pour prendre conscience de l’écart entre ce que prédit la complexité dans le pire des cas et le comportement en pratique, représenté par la complexité amortie.
Pire, on voit que de simples petites idées, comme les deux heuristiques utilisées par Union-Find, peuvent modifier drastiquement la complexité amortie tandis que la complexité dans le pire des cas reste la même voire augmente.
Insistons sur les différences avec l’analyse en moyenne
De prime abord, la différence entre l’analyse amortie et l’analyse en moyenne peut ne pas sembler flagrante. Je me permets donc d’insister sur les éléments distinctifs : le niveau de granularité étudié et surtout, la notion d’état. Dans le cas de l’analyse en moyenne, on étudie la répartition des instances difficiles en supposant (ou estimant) une distribution de probabilité sur l’ensemble des instances. En d’autres termes, on s’intéresse aux instances. Dans le cas de l’analyse amortie, on considère $n$ étapes au sein d’un algorithme et l’on s’intéresse à comment en moyenne les opérations coûteuses et non-coûteuses peuvent se compenser. On est à un niveau de granularité plus faible, ce qui est rendu possible par le fait que l’on considère des étapes d’un algorithme qui sont liées entre elles par la modification d’un état (par exemple la mémoire dans l’exemple du tableau dynamique).
Ainsi l’analyse amortie est particulièrement utile pour les structures de données et les algorithmes qui maintiennent un état en évolution tout au long de leur exécution. Les deux approches peuvent donc être complémentaires.
Analyse lisse
Si la complexité en moyenne a été introduite pour pallier certaines limitations de la complexité dans le pire des cas, la complexité lisse a pour but d’être une synthèse permettant d’outrepasser les limitations des mesures de complexité précédentes et notamment en expliquant pourquoi certains algorithmes restent efficaces en pratique contrairement aux études théoriques effectuées jusque-là.
Développée dans les années 2000, l’analyse lisse consiste à étudier le comportement d’un algorithme sur un ensemble d’instances en les perturbant légèrement de manière aléatoire.
Plus formellement, on suppose que l’on dispose d’un opérateur $K$ de perturbation aléatoire sur l’ensemble $\Pi_n$ des instances de taille $n$. Cela permet de définir une espérance sur le nombre d’opérations, exprimée par $\forall \pi \in \Pi_n, ~ \bar \pi = E[T(K\pi)]$.
Alors la complexité lisse d’un algorithme sur $\Pi_n$ est donnée par :
Elle est donc relative à un opérateur de perturbation choisi.
Supposons que l’on puisse métriser l’espace $\Pi_n$ avec une distance $d$ et que notre opérateur de perturbation soit paramétré par une variance $\sigma$ qui mesure l’amplitude de perturbation. Autrement dit $\forall ~ 0 \leq \sigma_1 \leq \sigma_2,~ d(K_{\sigma_1}\pi,\pi) \leq d(K_{\sigma_2}\pi, \pi)$ presque sûrement4. Ainsi lorsque $\sigma$ tend vers 0, $d(K_\sigma\pi,\pi)$ tend vers $0$, ce qui signifie alors que $K$ est équivalent à l’identité : $K\pi = \pi$.
Alors, on remarque que lorsque $\sigma$ tend vers 0, on retrouve la complexité dans le pire des cas :
Dans le cas où $\sigma$ tend vers l’infini, on retrouve la complexité en moyenne.
Exemple de perturbation : Considérons que $\Pi_n = \mathbb{R}^n$ qui est un domaine très courant en simulation numérique, optimisation ou traitement du signal par exemple. L’opérateur de perturbation gaussien est défini comme $K_{\sigma^2} : \mathbb{R}^n \to \mathbb{R}^n$ avec $K_{\sigma^2} : \pi \mapsto \pi + g$ où $g$ est un vecteur gaussien centré de dimension $n$.
Malheureusement, avec l’intervention de l’opérateur $K$ qui est lui-même paramétré, il faut changer quelque peu la définition de complexité polynomiale pour lui donner un sens au sein de l’analyse lisse.
Définition : L’algorithme $A$ a une complexité lisse polynomiale s’il existe des constantes $n_0$, $\sigma_0$, $c$, $k_1$ et $k_2$ telles que pour tout $n > n_0$ et $ 0 \leq \sigma \leq \sigma_0,~ T^{K_{\sigma^2}}_{lis}(n) \leq c \frac{n^{k_1}}{\sigma^{k_2}}$.
L’intérêt d’une formulation probabiliste est que l’on peut faire intervenir les outils habituels et puissants de la théorie des probabilités. Par exemple, en appliquant l’inégalité de Markov5 à un algorithme qui possède une complexité lisse polynomiale, on obtient pour tout $\delta$ appartenant à $[0,1]$ :
Autrement dit, si $A$ a une complexité lisse polynomiale, alors il peut résoudre n’importe quelle instance perturbée en temps polynomial en $n$, $\frac 1 \sigma$ et $\frac 1 \delta$, avec une probabilité d’au moins $1 - \delta$.
L’intérêt d’une modélisation mathématique des problèmes prend alors tout son sens. Il peut être difficile dans des problèmes peu structurés ou non analytiques de faire ressortir une distance entre deux instances, et de fait, il devient alors impossible d’utiliser l’analyse lisse. À contrario, les problèmes utilisant des modèles mathématiques font souvent appel à des espaces classiques bénéficiant de métriques naturelles, et l'on peut définir la notion de problème bien posé. On verra un peu plus tard la nécessité d’une modélisation mathématique du problème pour l’étude de la difficulté du problème en amont.
Notons par ailleurs que l’algorithme du Simplexe a une complexité lisse polynomiale, ce qui montre que l’analyse lisse est capable de prédire les comportements des algorithmes de manière plus précise que les autres mesures évoquées.
Les défauts de la complexité pour la comparaison d’algorithmes
La complexité algorithmique asymptotique possède un certain nombre de défauts comme nous l’avons vu. Notamment, elle ne permet pas, sauf étude précise, une comparaison fiable entre deux algorithmes au sein d’une même classe de complexité (et parfois même en dehors), car elle masque des constantes qui vont avoir un impact pratique important. Le corollaire de cette remarque est qu’il peut être très difficile si ce n’est impossible de prédire le comportement réel de deux algorithmes sur un jeu d’instances d’un problème particulier.
Les pièges classiques
Prenons l’exemple d’un algorithme $A$ et $B$, de complexité dans le pire des cas $T_A(n) = 50n^2+50n+5000$ et $T_B(n) = n^3$, avec pour complexité asymptotique dans le pire des cas $\mathcal{O}(n^2)$ et $\mathcal{O}(n^3)$.
La figure suivante présente le tracé des deux complexités exactes en fonction de la taille du problème, ainsi que la courbe de la différence d’opérations nécessaires à la résolution du pire des cas. Si l’OGA indique que $A$ est meilleur que $B$, la réalité n’est pas tout à fait aussi claire. Si dans la partie précédente nous avons mis en avant le fait qu’il existe un point avant lequel l’algorithme ne se comporte pas comme son OGA, ici l’on montre qu’un algorithme peut être meilleur qu’un autre sur une plage de taille d’instance relativement grande malgré un OGA moins bon. Là encore, le « relativement » se définit par rapport à l’utilisation que l’on va faire de l’algorithme et de la taille des instances que l’on peut rencontrer en pratique.
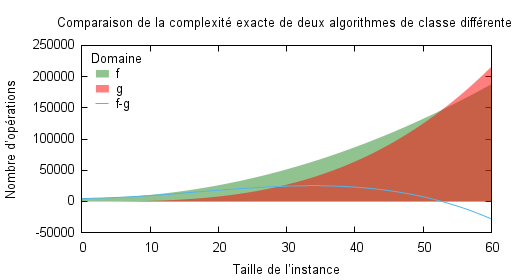
Il est clair que sur l’exemple précédent, jusqu’à des tailles d’instance environ égales à 53, l’algorithme $B$ est meilleur que l’algorithme $A$ et que si je sais à priori que la majorité des instances que je vais rencontrer vont être de taille inférieure à cette borne, alors j’ai tout intérêt à choisir l’algorithme $B$. Malheureusement, cette information n’est pas contenue dans l’OGA car ce n’est pas son rôle6.
L’exemple de la multiplication matricielle
Un second exemple, non artificiel cette fois, est le problème de la multiplication matricielle. Si l’algorithme de Coppersmith-Winograd a une complexité en $\mathcal{O}(n^{2.376})$, l’algorithme de Strassen possède lui une borne asymptotique donnée par $\mathcal{O}(n^{2.807})$. On pourrait donc s’attendre à ce que Strassen soit plus lent en pratique que Coppersmith-Winograd. En réalité, c’est le contraire qui se produit car, pour ce dernier, des constantes multiplicatives et des termes d’ordres inférieurs fortement pondérés interviennent et augmentent la limite inférieure à partir de laquelle on peut considérer que l’algorithme est en régime aymptotique. Et ces termes sont tellement importants qu’en pratique la dimension des matrices telles que Coppersmith-Winograd est plus intéressant que Strassen est telle que personne n’en a d’utilité aujourd’hui7.
Pire, même une étude précise pourra être mise en défaut par l’évaluation empirique, et ce d’autant plus facilement que les deux algorithmes comparés offrent une complexité proche. Les facteurs qui propagent un peu plus cette incertitude sont bien évidemment l’abstraction matérielle, l’abstraction des implémentations de briques logicielles d’un niveau de granularité plus faible, comme des opérations sur les structures de données voire les structures de données elles-mêmes dont on ne dispose pas toujours de l’implémentation, et évidemment, les optimisations matérielles et logicielles qui vont réarranger les opérations voire les remplacer par d’autres pour des gains généralement variables d’une implémentation à l’autre et plus encore d’une implémentation d’un algorithme A à l’implémentation d’un algorithme B.
Ces détails font qu’il faut relativiser très grandement la complexité d’un algorithme dans la pratique vis-à-vis de la prédiction du temps qu’elle peut fournir. Plus les systèmes deviennent complexes, de même que les algorithmes ou les problèmes qu’ils résolvent et plus du bruit s’ajoute par la force des choses à l’étude théorique de la complexité algorithmique. Et ce bruit n’arrive pas à être capté et explicité par cette notion comme en témoigne l’exemple typique de l’algorithme du Simplexe et des points intérieurs évoqués en introduction. À sa décharge, ce n’est pas le but de la complexité algorithmique que de pouvoir donner une prédiction précise du temps de calcul.
-
Pour une définition plus formelle, on renvoie un cours sur le sujet. ↩
-
Parfois on utilise non pas $T_{\text{max}}$ mais $\bar T$ et l’on parlera alors de coût moyen amorti. Cela doit vous faire sentir qu’il ne s’agit pas tout à fait de la même chose. ↩
-
En réalité on a besoin que de la convergence en loi qui est bien plus faible. ↩
-
Soit $X$ une variable aléatoire réelle, presque surement positive, alors $\forall a > 0, ~ P(X \geq a) \leq \frac{E(X)}{a}$. ↩
-
Comme expliqué ici, Donald Knuth était favorable à l’utilisation d’un équivalent asymptotique et non un ordre de grandeur asymptotique pour exhiber l’influence de la constante multiplicative. ↩
-
Il est clair qu’étant donnée la taille croissante des instances de problèmes à résoudre, des algorithmes non-efficaces en pratique aujourd’hui mais asymptotiquement intéressants (typiquement polynomiaux) pourront trouver leur utilité dans un futur plus ou moins proche. ↩
Vers des critères de difficulté en amont
Est-il possible de caractériser la difficulté d’un problème sans avoir d’algorithme pour le résoudre ? Peut-on prédire le comportement d’algorithmes types sur un problème donné en amont ? Je propose ici quelques concepts et idées qui permettent de répondre par l’affirmative à ces questions sur des catégories de problèmes particuliers. La démarche est donc en général de transformer l’énoncé d’un problème en formulation mathématique, puis de se ramener à un autre problème type dont a déjà étudié les caractéristiques ou donné des preuves sur le comportement attendu d’un certain nombre de méthodes de résolution.
Des problèmes de décision vers l’optimisation
Présentons une version plus générale du plus problème d’optimisation, dont nous avons abordé le cas particulier qu’est le problème d’optimisation linéaire.
Soit $\Omega$, un espace dit des variables de décision, $X \subset \Omega$ une partie de l’espace de décision souvent appelé espace admissible, et $Y$ un espace totalement ordonné appelé espace objectif, souvent $\mathbb{R}$. Soit $f:\Omega \to Y$, alors le problème de minimisation consiste à minimiser $f$ sur $X$, c’est-à-dire trouver $f^{*} = \underset{x \in X}{\text{min}}~f(x)$ (sous réserve d’existence de cette valeur) et éventuellement l’ensemble des éléments permettant de réaliser cette valeur optimale, c’est-à-dire $S = \{ x \in X ; f(x) = f^{*} \}$.
L’intérêt de ce problème est qu’il est toujours possible en pratique de se ramener à cette formulation, même de manière artificielle. S’il est évident que pour des problèmes classiques du type trier un tableau, le problème a été étudié spécifiquement et des algorithmes très spécifiques ont vu le jour, l’étude d’une formulation sous forme d’optimisation peut parfois aider à l’élaboration de nouveaux algorithmes ou à une meilleure compréhension du problème.
Un problème de décision est un problème dont la réponse est soit « oui » soit « non ». Pour chaque problème de cette catégorie, on peut montrer qu’il existe au moins un problème d’optimisation associé. Par exemple, pour le problème de décision « le tableau $T$ est-il trié ? » $(PD)$, une formulation sous forme d’un problème d’optimisation pourrait être « maximiser la séquence d’éléments triés au sein de $T$ » $(PO)$. Dès lors, lorsque l’on atteint le maximum de $(PO)$ cela équivaut à répondre « oui » à $(PD)$ et si le minimum n’est pas atteint, alors la réponse à $(PD)$ est « non ». Autrement dit, on résolvant $(PO)$ on résout exactement $(PD)$.
Évidemment, le problème initial peut éventuellement se mettre directement sous forme d’un problème d’optimisation, de même que pour un problème de décision, il peut exister plusieurs formulations d’optimisation dont certaines peuvent être plus aisées à manipuler ou proposer des propriétés intrinsèques plus intéressantes. C’est là qu’intervient le travail de modélisation du mathématicien ou de l’ingénieur en mathématique dont les choix de modélisation proviennent principalement de la connaissance des problèmes récurrents. L’important est plutôt de saisir l’infinité des problèmes qui peuvent se formuler in fine comme un problème d’optimisation et donc l’importance que revêt cette branche des mathématiques pour les applications aussi bien en informatique qu’en physique ou en science sociale.
Linéarité versus non linéarité
En premier lieu, rappelons la définition de la linéarité d’une fonction. Une fonction $f$ est linéaire si elle satisfait le principe de superposition, c’est-à-dire si $\forall x,y,\alpha \in \mathbb{R},~ f(x+\alpha y) = f(x) + \alpha f(y)$.
L’ensemble admissible $X$ est obtenu par l’application de contraintes sur $\Omega$ (et si aucune contrainte ne s’applique, $X = \Omega$). Par exemple, dans le cas de l’optimisation linéaire évoqué plus haut, c’est l’intersection d’hyperplans (qui, en dimension 2, sont des droites) qui délimite et caractérise $X$ au sein de l’ensemble $\Omega$.
Mais l’on peut imaginer contraindre $\Omega$ par d’autres types de fonctions. Imaginons que $\Omega$ soit un jardin, carré, dont la longueur d’un côté est $L$, et qu’au centre soit attaché à un pilier un chien au bout d’une laisse de longueur $l \leq \frac L 2$. L’ensemble des positions que le chien peut adopter, c’est-à-dire l’ensemble $X$, est défini par les points de coordonnées $x^2 + y^2 \leq l$, autrement dit le disque de rayon $l$ et de centre le pilier. Par ailleurs, la contrainte de la laisse attachée au pilier sur la position du chien est non linéaire. Un exemple de fonction que l’on voudrait maximiser serait $f(.,.)$ définie comme la distance entre le chien et le pilier central. Il est évident que le maximum est atteint en tout point du cercle $x^2 + y^2 = l$.
On dira qu’un problème d’optimisation est linéaire lorsque toutes les contraintes qui s’appliquent à $\Omega$ pour obtenir $X$ sont linéaires et que la fonction $f$ à optimiser est linéaire. L’optimisation linéaire est donc un cas très particulier d’optimisation.
Qu’est-ce qu’un problème facile ?
La facilité d’un problème comme caractéristique n’est pas une notion qui trouve un formalisme rigoureux. On se contente de qualifier un problème de facile lorsqu’il répond à certaines caractéristiques mathématiques. La notion de facilité n’est donc pas tout à fait binaire – facile ou difficile – mais plutôt un agrégat de propriétés intéressantes dont on cite quelques-unes des plus importantes :
-
Existence de solution : le problème admet-il une solution ? La question peut faire sourire, mais il existe bien des problèmes où l’existence même d’une solution n’est pas facilement démontrable ! Un problème facile aura une preuve d’existence de solution sans condition1 et des algorithmes rapides pour tester si la solution existe. C’est le cas de l’optimisation linéaire. Au contraire, des problèmes difficiles n’auront pas ces preuves d’existence, ou alors sous des conditions qui en limitent l’application. Tester l’existence de solutions peut dès lors requérir un temps exponentiel.
-
Problème multi-modal : le problème possède-t-il plusieurs solutions (appelées modes) ? Il est en effet possible que plusieurs éléments de $X$ donnent la valeur optimale pour $f$. C’est le cas de la simple fonction valeur absolue où le maximum sur $[-5,5]$ par exemple, est obtenu autant par $x=5$ que $x=-5$. La résolution de problèmes multi-modaux avec pour critère l’obtention de toutes les solutions réalisant le minimum est en général un problème très difficile que seules les méthodes d’intelligence calculatoire de type algorithmes évolutionnaires arrivent à résoudre de manière efficace.
Ainsi, l’existence de plusieurs modes est caractéristique de problèmes plus difficiles que les problèmes n’ayant qu’un mode.
Ne parlons alors pas des problèmes multi-objectifs qui sont de facto multi-modaux puisqu’il n’existe pas en général une solution mais un ensemble de solutions, réalisant un équilibre ou compromis, appelé l’ensemble de Pareto. On comprendra dès lors que les méthodes les plus efficaces pour ces problèmes sont une fois encore des techniques de type algorithmes génétiques, sauf cas particuliers.
En général les méthodes adoptées pour résoudre ces problèmes sont basées sur des suites itératives $(x_n)$. Il s’agit de suites qui vont se rapprocher itération après itération de l’extremum (on parle de suite minimisante ou maximisante et par définition de l’extremum une telle suite existe) et dont on espère beaucoup de propriétés pour résoudre le problème d’optimisation :
-
Convergence vers un minimum : la suite minimisante $x_n$ converge vers un infimum mais le minimum est-il atteint ?
-
Conditions de convergence : la suite converge-t-elle sans condition ?
-
Convergence finie ou infinie : converge-t-on nécessairement en un nombre fini d’étapes ?
-
Vitesse de convergence : à quelle vitesse va-t-on obtenir la solution, pour une précision donnée ? Il s’agit alors d’essayer de trouver le majorant le plus fin possible de $d(x_{n+1}, x^*)$ en fonction de $d(x_{n}, x^*)$. Par exemple, dans le cas de la méthode de Newton, sous réserve que l’on puisse appliquer la méthode, on peut montrer que $d(x_{n+1}, x^*) \leq Cd(x_n, x^*)^2$, autrement dit la vitesse est quadratique.
Notons que les réponses à ces questions relèvent autant de la construction de la suite que de des propriétés de l’espace $X$. Par exemple, le minimum est atteint lorsque l’on travaille sur des ensembles fermés bornés en dimension finie car ceux-ci sont alors compacts, tandis que d’autres propriétés sont requises en dimensions infinie, notamment… la convexité de $X$. On renvoie le lecteur désireux d’en savoir plus sur ce passionnant sujet à des cours d’optimisation qui fourmillent sur Internet. On pourra recommander « Analyse numérique et optimisation » de Grégoire Allaire dont une version amoindrie des illustrations est disponible pour l’usage personnel sur le site de l'auteur donné en référence.
La partie algorithmique n’est finalement que la partie qui consiste à construire une telle suite. Le que est à modérer par le fait que généralement, les résultats donnés mathématiquement sont rarement constructifs, c’est-à-dire qu’ils ne permettent pas de construire une telle suite. Il reste donc un travail à faire pour appliquer ces résultats de manière informatique dans bien des cas.
Une question de domaine
Durant des années, on a pensé que la difficulté intrinsèque d’un problème était liée majoritairement à la propriété de linéarité, les problèmes linéaires étant les problèmes faciles à résoudre. Cependant, au fur et à mesure que les résultats théoriques apparaissent, notamment dans le domaine de l’analyse fonctionnelle (en particulier, voir Analyse fonctionnelle : théorie et applications de Haïm Brezis), il est devenu de plus en plus clair que ce qui caractérisait la difficulté du problème était la nature de $X$ plus que les contraintes s’appliquant à $\Omega$ dont $X$ résulte.
Clarifions : l’exemple du programme d’optimisation linéaire permet d’obtenir un domaine $X$ sous la forme d’un polyèdre, donc convexe par définition. Dans l’exemple du chien et de la laisse, le domaine $X$ est un disque, qui reste un domaine convexe. L’un est obtenu à partir uniquement de fonctions linéaires, tandis que le second uniquement à partir de contraintes quadratiques ; et pourtant ces deux problèmes sont simples : ce n’est donc pas la propriété de linéarité qui implique la simplicité mais une autre propriété commune à ces problèmes, à savoir, la convexité.
La fonction $f$ étant agnostique aux contraintes s’appliquant sur $\Omega$ pour obtenir $X$, ce n’est donc pas en étudiant la linéarité que l’on peut caractériser la difficulté d’un problème mais en étudiant la topologie du domaine $X$, couplée aux propriétés de $f$ (il convient cependant de rester prudent puisque l’étude des contraintes est loin d’être inutile). C’est ainsi que les frontières de l’optimisation se sont redessinées au sein de la recherche. Par le passé, l’optimisation linéaire était séparée artificiellement de l’optimisation non-linéaire, mais aujourd’hui, malgré le fait que l’on enseigne toujours en premier lieu et de manière assez séparée l’optimisation linéaire, la frontière serait plutôt l’optimisation convexe et l’optimisation non-convexe2.
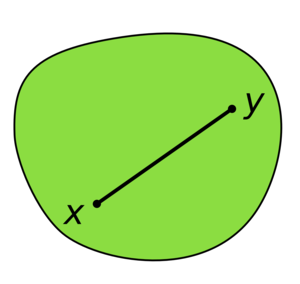
"…in fact, the great watershed in optimization isn’t between linearity and nonlinearity, but convexity and nonconvexity." – R. Tyrrell Rockafellar, in SIAM Review, 1993
La chose remarquable qu’il faut constater, c’est qu’il est mathématiquement bien plus facile de résoudre les problèmes sur des domaines convexes car ils possèdent maintes propriétés très intéressantes, dont certaines citées plus haut telles que l’existence d’une solution. Si en plus d’être convexe, le domaine est un polyèdre alors on peut montrer que la solution est unique et appartient à l’enveloppe convexe, qui est dans ce cas un polytope, pour citer une autre propriété bien connue.
À contrario, les problèmes non-convexes sont fondamentalement difficiles, c’est-à-dire fondamentalement inextricables (de l’anglais untractable), ce qui signifie qu’il n’existe pas d’algorithme qui puisse les résoudre en temps polynomial. Pour ces problèmes, le temps minimal nécessaire à la résolution pour tout algorithme possible (et non connu) est une fonction qui croit plus vite qu’un polynôme. Par abus de langage, un problème est inextricable si le meilleur algorithme connu à ce jour a une complexité en temps exponentiel.
Le problème de la tour de Hanoï a été prouvé comme étant inextricable3, tandis que l’on suppose que le problème du voyageur de commerce est inextricable, mais l’on ne dispose pas de preuve pour cela.
Inutile de dire que la plupart des applications pratiques sont des problèmes non-convexes et donc majoritairement inextricables.
Convexe versus non-convexe
Remarquez que l’on parle en général d’optimisation non-convexe et non pas d’optimisation concave car la plupart des problèmes non-convexes ne sont pas concaves et sont tout aussi difficiles à résoudre que ces derniers.
La question qui se pose est alors : pourquoi les problèmes convexes sont faciles ? La réponse tient dans les outils mathématiques dont on dispose et qui permettent l’élaboration de méthodes efficaces dans tous les cas.
Le point de départ pour expliquer tient dans l’unique théorème de Hahn-Banach sur la séparation des convexes.
Théorème : Soit $E$ un espace normé, $A$ et $B$ deux convexes de $E$ non vides et disjoints. On suppose $A$ ouvert. Alors il existe un hyperplan fermé séparant $A$ et $B$.
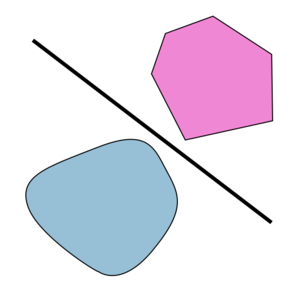
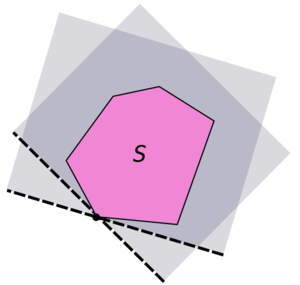
Une version plus faible, ne supposant pas l’ouverture de A, permet d’obtenir le même résultat de séparation, mais par un hyperplan qui n’est pas nécessairement fermé. En particulier, il est possible de séparer un singleton de la frontière d’un convexe avec le reste du convexe.

Dès lors, on peut définir la notion d’hyperplan d’appui et, de fil en aiguille, définir le sous-différentiel en un point de la frontière du convexe comme l’ensemble des coefficients des pentes des hyperplans d’appui en ce point. Il ne s’agit pas d’entrer plus dans les détails, cet article concernant avant tout la complexité algorithmique, mais plutôt de donner quelques pistes de recherche pour le lecteur désireux d’en savoir plus.
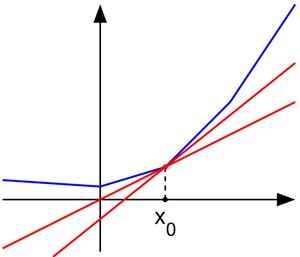
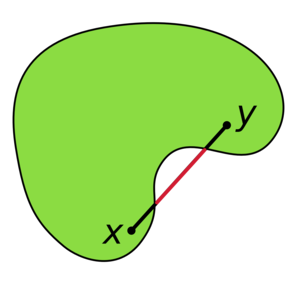
Au contraire, sur des espaces non-convexes, on peut trouver des points de la frontière pour lesquels le sous-différentiel n’existe pas, tout simplement car il n’existe pas d’hyperplan d’appui, comme illustré sur la figure ci-dessous.
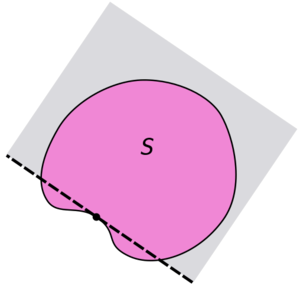
Pour illustrer la difficulté que l’on peut rencontrer sur les problèmes dont le domaine possède des parties concaves, l’optimisation multi-objectif est particulièrement parlante. Dans un tel cas, la particularité est que l’on cherche l’ensemble des points de la frontière du domaine, qui tous, réalisent un équilibre de Pareto. Sur l’animation suivante, il s’agit de toute la frontière visible de l’espace objectif.
Une technique naïve utilisée est d’agréger les objectifs pour former une nouvelle fonction objective scalaire, ce qui permet d’utiliser les méthodes « classiques » des problèmes mono-objectifs. Toujours naïvement, on utilise souvent une combinaison linéaire des objectifs, c’est-à-dire que si l’on dispose de deux objectifs à notre problème que sont $f_1$ et $f_2$ alors la fonction que l’on utilisera sera $f = \omega_1f_1 + \omega_2 f_2$ avec $\omega_1 + \omega_2 = 1$. Or, l’illustration suivante montre qu’en utilisant une fonction d’agrégation qui est une combinaison linéaire des objectifs, il est impossible d’atteindre la partie concave du front4.
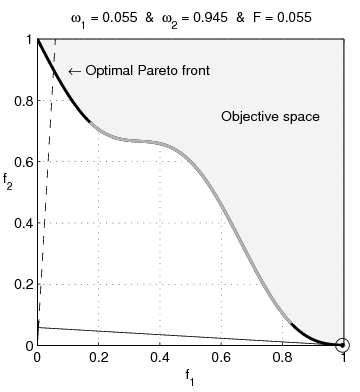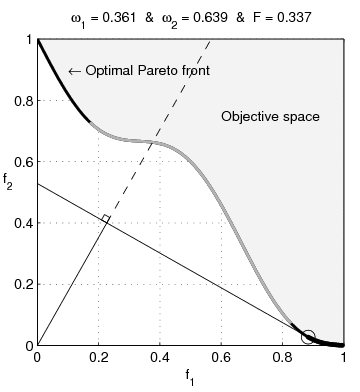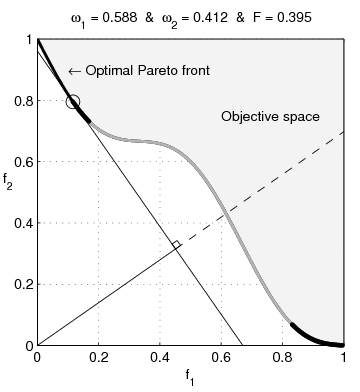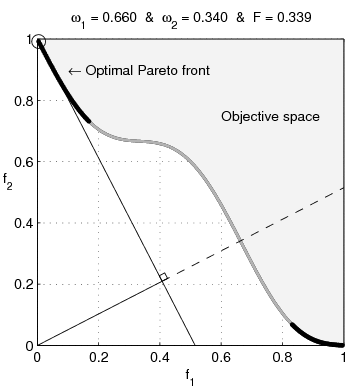
De manière plus générale, un domaine non-convexe va impliquer possiblement de nombreux optimums locaux dans lesquels les algorithmes habituels vont être piégés, comme c’est le cas de l’algorithme de Newton. Détecter si un optimum n’est pas local est un problème inextricable dans le cas non-convexe. Bref, les propriétés pour qualifier un problème de facile sont toutes mises à défaut beaucoup plus facilement que pour le cas convexe.

Sur la figure ci-dessus, représentant une fonction multimodale, selon le point de départ de la méthode de Newton, celle-ci va converger vers un des quatre optimums possibles du domaine, mais seul l’un d’entre eux est un optimum global. Il existe une zone autour de chacun de ces points que l'on nomme bassin d'attraction (lien anglais) et qui « capture » la suite qui s’aventure en son sein.
-
Attention, cela ne veut pas dire que la solution existe toujours, mais que les critères sont indépendants de l’instance du problème. ↩
-
Il ne faut cependant pas trop prêter attention à ces séparations. Les seules séparations valables sont celles qui séparent deux catégories de problèmes par rapport aux outils disponibles pour les résoudre et ainsi, en fonction du temps ces frontières changent, ou plus précisemment reculent. Le travail de la recherche étant d’étendre les outils déjà existants à des problèmes plus difficiles, d’en proposer de nouveaux, ce qui permet d’unifier des domaines. ↩
-
Ce problème n’appartient pas à $NP$ et donc ne peut pas être $NP$-Complet. De fait, savoir qu’il n’existe pas d’algorithme polynomial pour ce problème n’a aucune incidence sur le problème ouvert $P=NP$. ↩
-
Il existe cependant un tas de raffinements qui permettent d’atteindre ces zones, avec plus ou moins de difficultés mais nous n’entrons pas dans les détails ici et renvoyons à un cours sur l’optimisation multi-objective. ↩
Robustesse théorique et empirique d’un algorithme
Comme nous l’avons vu, la notion pertinente pour caractériser la difficulté d’un problème est la notion de convexité, et non pas celle de complexité des algorithmes pour le résoudre, qui en est généralement une conséquence. Cependant, comme suggéré, on peut tout de même raffiner en étudiant les caractéristiques du domaine de notre problème, en sus de la convexité.
Par exemple, si l’optimisation continue est en générale plus facile que l’optimisation combinatoire c’est parce que l’on possède le concept de dérivée ou plus precisément de gradient. Mais même en optimisation continue, si le domaine de notre instance possède trop d’irrégularités ou un certain nombre de pathologies, les méthodes habituellement efficaces peuvent connaître des difficultés allant d’un temps empirique bien plus grand qu’en moyenne jusqu’à l’impossibilité d’être appliquées (nécessite l’existence d’une dérivée d’ordre supérieur par exemple). Des exemples de domaines pathologiques peuvent être visualisés ici, ici ou encore ici.
On aimerait donc caractériser la robustesse d’un algorithme par rapport au problème qu’il résout, en fonction de sa capacité à ne pas varier de manière trop significative en fonction des instances du problème. On entend principalement donner des résultats empiriques temporels qui varient peu quelles que soient les instances de tailles similaires que l’algorithme résout, autrement dit, une variance faible sur le temps de résolution.
Les pistes de recherche actuelles semblent indiquer que cette robustesse est obtenue par des propriétés d’invariance possédées par l’algorithme. Dans le cas de l’optimisation, on peut citer quelques exemples :
- Invariance par une transformation de la fonction objectif : plus la transformation préservant l’invariance a des propriétés générales et plus l’algorithme sera robuste. Par exemple, une translation est une transformation plus stricte que la transformation par une fonction strictement monotone et donc un algorithme qui n’a pour invariant que la translation est moins robuste qu’un algorithme invariant pour la transformation de la fonction objectif par une fonction strictement monotone.
- Invariance par transformation de l’espace de recherche : il s’agit typiquement de rotations, réflexions, translations ou une composition de celles-ci.
On comprendra donc que ces propriétés d’invariance offertes par les algorithmes sont hautement désirables puisqu’elles permettent d’obtenir une généralisation des résultats empiriques à toutes les instances de la même classe par rapport à la relation d’invariance. Pour donner un exemple, si un algorithme supporte une propriété d’invariance par translation de la fonction objectif, alors cela veut dire que cet algorithme aura des performances équivalentes sur la fonction $f$ et les fonctions $f_a$ définies par $f_a(x) = f(x) + a$ quel que soit $a \in \mathbb{R}$.
Notez que cette notion d’invariance est une indication théorique permettant de caractériser les performances empiriques là où la complexité échoue généralement au passage à l’empirique comme le montre le contre-exemple de l’algorithme du Simplexe.
En réalité il y a bien une notion de complexité qui se rapproche de la robustesse par invariance et c’est l’analyse lisse d’algorithmes. En effet, on peut considérer que l’opérateur de perturbation est une transformation particulière, aléatoire notamment.
Il s’agit non pas d’une étude de transformation générale mais de l’étude d’une classe de transformation particulière que l’on peut qualifier de perturbation locale, souvent gaussienne. La différence est que dans l’analyse lisse on s’intéresse au pire des cas obtenu par perturbation tandis que dans l’étude d’invariance on étudie des classes d’équivalence pour la transformation considérée, non aléatoire, sans tenir compte de la complexité.
Une deuxième piste pour caractériser la robustesse d’un algorithme est sa capacité à être paramétré rapidemment (et donc plus ou moins, de manière corrélée, à proposer peu de paramètres et des paramètres à domaine restreint).
No Free Lunch
Si l’on se place à une échelle un peu plus large, de nombreuses méthodes ont été conçues pour appréhender de nombreux problèmes différents. On parle alors de « métaheuristiques ». « Méta » pour la variété des problèmes que ces méthodes peuvent traiter, et « heuristiques » car elles n’offrent, en général, pas de garantie de performance et se contentent d’une solution approchée. Malgré cela, et la complexité exponentielle d’un grand nombre de ces méthodes, elles permettent d’obtenir de très bons résultats pour les applications pratiques, sur des problèmes en général intraitables par les méthodes classiques. Ce sont par exemple les méthodes de prédilection pour l’optimisation non-lisse, c’est-à-dire les problèmes d’optimisation sur des domaines très irréguliers mettant en défaut des méthodes plus classiques.
On est alors en droit de se demander s’il existe une méthode qui permet d’obtenir de meilleurs résultats pour tous les problèmes d’un ensemble de problèmes donnés, auquel cas les autres méthodes deviendraient obsolètes. La réponse est non et est apportée par le célèbre théorème du No Free Lunch (lien anglais) qui affirme qu’à moins d’exploiter l’information disponible au niveau d’un problème particulier, il n’existe pas de métaheuristique qui soit intrinsèquement meilleure qu’une autre.
Le corollaire est que l’exploitation de l’information inscrite dans le problème ou dans ses instances est nécessaire pour « optimiser » un algorithme sur un problème ou un jeu d’instances donné. Par ailleurs, les métaheuristiques étant des méthodes approchées, elles sont souvent réglées empiriquement par un nombre important de paramètres qui constituent un obstacle pour l’utilisateur final.
Dès lors, ce sont de bons candidats pour un domaine qui se développe de plus en plus, à savoir la méta-optimisation.
Compromis conception-exploitation
Ce qui n’est pris en compte par aucune notion de complexité algorithmique c’est le temps nécessaire au réglage de l’algorithme. Un algorithme évolutionnaire possède souvent un nombre très important de paramètres. Parmi les plus généraux et que l’on retrouve sur presque toutes les méthodes : la taille de la population, les probabilités de mutation et de croisement, etc.
Dès lors, pour en tirer le meilleur sur une situation pratique (la phase d’exploitation) il faut calibrer l’algorithme (la phase de conception). Et l’on se retrouve de fait avec un compromis à faire : le temps accordé à la recherche des meilleurs paramètres versus la qualité des paramètres trouvés. Si l’on reprend l’exemple des paramètres de taille de population et des deux probabilités, en considérant des tailles de population qui varient de 10 à 100 individus, et une discrétisation par pas de 0.1 pour les probabilités, on obtient déjà un espace de configuration de taille $90 \times 11 \times 11 = 10890$, que l’on devrait multiplier par le nombre d’instances possibles du problème, possiblement discrétisées dans le cas continue. Il est donc impossible, même lorsqu’il y a peu de paramètres, d’explorer explicitement toutes les configurations.
La méta-optimisation (lien anglais) consiste donc à élaborer des méthodes pour rapidement trouver des paramètres de bonne qualité. On parle également plus généralement de parameter tuning en anglais. Comme il ne s’agit pas de l’objet de cet article, on n’entrera pas plus dans les détails sur les diverses techniques d’optimisation de paramètres, mais l’on se contentera de faire la remarque suivante : un algorithme est d’autant plus robuste qu’il est d’une part rapide à optimiser et, d’autre part, que ses paramètres sont peu sensibles, c’est-à-dire vont jouer un rôle limité dans les résultats obtenus.
La facilité à être optimisé provient surtout des invariances évoquées plus haut puisque si un algorithme donne de bons résultats sur une instance avec une configuration donnée, toutes les instances résultantes par invariance donneront les mêmes résultats pour cette même configuration. Dès lors, les invariances font diminuer l’espace de recherche des algorithmes de méta-optimisation. La facilité provient également d’un faible nombre de paramètres à optimiser. Une technique de réduction du nombre de paramètres consiste en des méthodes qui optimisent le paramètre en même temps que l’algorithme recherche la solution au problème : on parle de méthode en ligne (online en anglais). Dès lors, l’utilisateur final n’a plus à se soucier de ce paramètre qui va s’auto-calibrer sans l’aide de personne. Ou presque… puisque la plupart des méthodes en ligne font apparaître de nouveaux paramètres, souvent plus nombreux. L’intérêt est alors que ces méta-paramètres sont moins sensibles que leurs homologues de premier ordre, c’est-à-dire que leur modification entraine de plus petites variations en moyenne dans les résultats que l’on peut espérer obtenir.
Signalons au lecteur l’existence de logiciels dédiés à l'optimisation de paramètres comme ParamILS.
Conclusion
Que peut-on tirer comme leçon de cet article ? Tout d’abord, son but premier était de montrer que la notion de complexité la plus courante, celle dans le pire des cas, est très facilement mise à défaut et que c’est normal ! Elle ne cherche pas à permettre de comparer deux algorithmes mais à donner une indication sur la capacité de l’algorithme à évoluer avec la taille des problèmes. On ne peut pas en tirer beaucoup plus d’informations que la classe de complexité d’un algorithme, et ainsi les conséquences sur la dynamique des performances en fonction de la taille du problème. J’insiste sur le mot dynamique comme pour dire qu’il s’agit d’une caractéristique qualitative plus que quantitative : la complexité dans le pire des cas ne permet pas de faire des prévisions efficaces mais simplement de prédire la scalabilité.
Il existe cependant d’autres notions de complexité, développées pour combler les lacunes de leur prédécesseur sur sa capacité à faire le lien entre théorie et application. Si chacune possède également des défauts, elles sont un pas en avant vers une meilleure caractérisation en amont de la capacité des algorithmes à bien se comporter en pratique.
Cependant, une caractérisation encore plus en amont, au niveau des problèmes, est souvent souhaitable car cela permet d’anticiper les capacités des algorithmes qui vont résoudre ces problèmes. La caractéristique principale pour qualifier un problème de facile est la convexité de celui-ci. À contrario, les problèmes non-convexes seront généralement très difficiles et les algorithmes non efficaces, voire dans le pire des cas, aucun algorithme efficace ne peut exister.
Enfin, avec la multiplication des problèmes non-convexes, des techniques satisfaisantes en pratique ont vu le jour, mais celles-ci ont un besoin de calibration qui n’est pas retranscrit par la complexité algorithmique. En réalité, les besoins dans beaucoup de domaines pratiques ne sont plus les mêmes qu’il y a 50 ans, et la complexification des problèmes, du matériel sur lequel va être exécuté un algorithme, et des algorithmes eux-mêmes, ont fait émerger de nouveaux besoins et critères de qualité et de robustesse.
La complexité algorithmique n’est plus alors qu’une métrique parmi d’autres et ne devrait plus, dans bien des cas, être considérée comme un facteur décisif pour définir la qualité d’un algorithme ou d’une méthode. Les progrès en mathématiques ont également permis de déplacer l’étude de l’efficacité du couple problème-méthode de la méthode vers le problème. Pas entièrement, mais suffisamment pour que cela soit d’un intérêt pour le plus grand nombre de connaitre à minima les avancées de ces travaux et la classification des problèmes faciles selon ces nouveaux critères.
Références
- Smoothed Analysis: An Attempt to Explain the Behavior of Algorithms in Practice
- Smooth Analysis Homepage
-
Smooth Analysis of Algorithms: Why the Simplex Algorithm Usually Takes Polynomial Time
- Impacts of Invariance in Search: When CMA-ES and PSO Face Ill-Conditioned and Non-Separable Problems
- No Free Lunch Theorems for Optimization
- Parameter Control in Evolutionary Algorithms
- Automatic Algorithm Configuration based on Local Search
Crédits des illustrations
- L’ensemble des images jusqu’à « Une question de domaine » et l'illustration de la fonction de Hölder ont été créés pour les besoins de cet article et placés dans le domaine public.
- Les illustrations de la partie « Une question de domaine » et celles de la section « Convexe versus non-convexe » représentant la séparation par hyperplan sont réalisées par Oleg Alexandrov et placées dans le domaine public.
- L’illustration du sous-différentiel d’une fonction convexe est réalisée par Maksim et est placée dans le domaine public.
- L’animation de la section « Convexe versus non-convexe » a été réalisée par Guillaume Jacquenot et est placée sous licence CC BY-SA 3.0. Aucune modification n’a été effectuée sur l’oeuvre.
- L’illustration du No Free Lunch Theorem a été réalisée par Johann Dréo et est placée sous licence CC BY-SA 3.0. Aucune modification n’a été effectuée sur l’oeuvre.






