En sciences, de nombreux phénomènes sont décrits par des équations différentielles dont la résolution exacte est parfois impossible ou peu intéressante. On laisse alors de côté les méthodes analytiques pour travailler directement avec des nombres, en utilisant ce qu’on appelle des méthodes numériques de résolution d’équations différentielles. Ces méthodes permettent notamment de simuler des systèmes physiques, ce qui en fait un outil puissant pour les sciences et l’ingénierie.
Ce tutoriel est une initiation à la simulation numérique, à travers la méthode la plus élémentaire qui soit : la méthode d’Euler explicite.
Il est destiné aux gens ayant déjà été initiés aux équations différentielles de manière formelle et souhaitant découvrir comment les résoudre autrement.
Ce tutoriel aborde les notions suivantes :
- discrétisation du temps,
- approximation de la dérivée selon la méthode d’Euler,
- schéma numérique d’Euler explicite,
- application pratique à une équation différentielle,
- précision, convergence et stabilité de la méthode d’Euler explicite sur un exemple.
Les prérequis nécessaires pour comprendre le tutoriel sont les suivants :
- résolution d’équations différentielles simples,
- suites numériques,
- notions élémentaires de physique (optionnel).
- Présentation de la méthode d'Euler
- Exemple travaillé : chute avec frottements fluides
- Précision et stabilité
Présentation de la méthode d'Euler
En guise d’introduction, je vous présente l’équation différentielle-type qui nous accompagnera tout au long de ce tutoriel :
Il s’agit d’une équation différentielle du premier ordre. La variable réelle représente le temps, compris entre zéro et une valeur limite ; est une fonction réelle du temps à déterminer, et est sa dérivée ; est une fonction réelle de et . On note la valeur initiale de , ce qui signifie simplement que .
Dans ce tutoriel, j’ai fait le choix d’utiliser une équation différentielle faisant apparaître des dérivées en fonction du temps , car beaucoup d’équations différentielles décrivent des évolutions temporelles. Cependant, la méthode s’applique tout aussi bien aux autres équations différentielles.
Sous des conditions généralement remplies en physique, cette équation différentielle admet une unique solution pour une condition initiale donnée.1 Il n’est donc pas vain d’essayer de résoudre cette équation différentielle !
L’équation différentielle ci-dessous est un exemple correspondant à l’équation-type vue précédemment, en prenant , où et sont des constantes.
Discrétisation du temps
Il est difficile pour un ordinateur de travailler avec des fonctions continues quelconques. Pour escamoter cet obstacle, il est courant de commencer par discrétiser le temps lors de la résolution numérique des équations différentielles (c’est notamment le cas dans la méthode d’Euler, qui nous intéresse ici). Autrement dit, on ne considère que certains instants particuliers, et on ignore ce qu’il se passe en dehors de ces instants. Formellement, on forme une suite croissante d’instants pris dans l’intervalle .

Ces instants peuvent a priori être choisis librement (par exemple toutes les secondes), mais la méthode de résolution numérique utilisée oriente en général ce choix. Notez que j’ai indexé cette suite dans , bien que les instants soient en nombre fini, car on peut en prendre autant que l’on souhaite.
Si l’on connaît une solution exacte de l’équation différentielle, elle prend évidemment la valeur à l’instant . La résolution numérique consiste à calculer approximativement les , et obtenir ainsi une solution numérique, qu’on espère fidèle à la solution exacte. La manière précise de calculer les dépend de la méthode de résolution utilisée. Formellement, on construit une suite de valeurs approchant les .
Pour la représentation graphique, on considère que la solution approchée est linéaire entre deux instants consécutifs. Notez bien que cette hypothèse n’est utilisée que pour tracer graphiquement la fonction, et n’est en aucun cas une hypothèse nécessaire pour utiliser la méthode d’Euler.
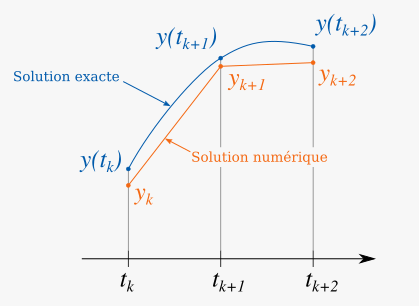
Approximation d’Euler
En choisissant de discrétiser le temps, nous sommes passés du monde des fonctions du temps à celui des suites numériques. Derrière cette apparente simplification se cache un obstacle à surmonter. En effet, le problème à résoudre est une équation différentielle, qui fait intervenir la notion de dérivée. Or cette notion fait intervenir la notion de limite (la dérivée est la limite, si elle existe, du taux d’accroissement), qu’on ne peut pas définir pour les suites.
Pour lever le problème, il faut adapter intelligemment l’opérateur de dérivation aux suites numériques ; c’est là que la méthode d’Euler entre véritablement en jeu. Dans sa variante dite explicite, que nous traitons ici, elle consiste à dire que le taux d’accroissement entre un instant et un instant ultérieur est égal à la dérivée à l’instant . Autrement dit, on approxime le taux d’accroissement à l’instant par :
La figure ci-dessous illustre cette approximation.
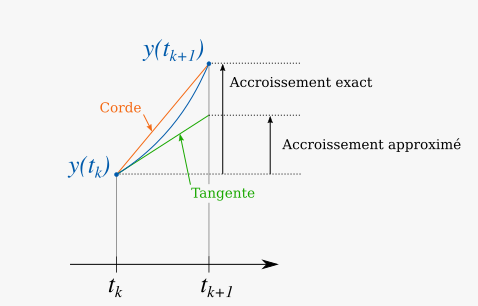
On peut déjà avoir l’intuition que l’écart entre deux instants ne saurait être trop important, au risque d’avoir une dérivée trop éloignée de la réalité ! Essayez de visualiser cela sur la figure précédente : en rapprochant de , l’accroissement approximé se rapproche de l’accroissement exact à mesure que la corde se rapproche de la tangente.
Discrétisation de l’équation différentielle
Nous avons maintenant tout le nécessaire pour transformer notre équation différentielle en suite récurrente, et compléter ainsi le passage du monde continu au monde des suites numériques.
Je vous rappelle ci-dessous l’équation différentielle que l’on cherche à résoudre numériquement sur l’intervalle :
En particulier, cette équation différentielle est vraie pour , de sorte que si est solution, vérifie l’équation suivante :
On applique l’approximation d’Euler pour faire disparaître la dérivée et obtenir une nouvelle équation, qui n’est vérifiée qu’approximativement par la solution exacte :
Bien qu’elle ne soit qu’approximative, cette équation est très utile, car elle donne une recette de cuisine pour fabriquer une solution approchée. En effet, on peut décider que la solution approchée vérifie cette égalité :
Ceci fait, on en déduit une relation de récurrence en gardant seulement à gauche et en transférant le reste dans le membre de droite. On appelle cette relation le schéma numérique d’Euler explicite :
est issu de l’étape précédente, les sont choisis librement, et est une fonction connue. On peut ainsi calculer de proche en proche en partant de la valeur initiale . Nous avons transformé une équation différentielle en une simple suite définie par récurrence ! Il se trouve que c’est une formulation très avantageuse pour un calcul par ordinateur, car ils sont justement conçus pour effectuer des opérations successives. C’est ce que nous ferons en passant à la pratique dans la partie suivante !
- Pour plus de détails, intéressez-vous au théorème de Cauchy-Lipschitz.↩
Exemple travaillé : chute avec frottements fluides
Position du problème
Considérons la chute verticale vers le bas d’un objet dans l’air, comme un caillou par exemple. L’objet est attiré par gravité vers le sol, mais il est aussi freiné par l’air, et il sera d’autant plus freiné que sa vitesse sera grande. On peut donc intuitivement penser que sa vitesse augmentera progressivement, avant d’atteindre une vitesse limite.
Pour vérifier cela, modélisons notre problème. L’objet a une masse , et est suffisamment dense pour qu’on néglige la poussée d’Archimède. Il est soumis au champ de pesanteur d’intensité ; il subit également une force de frottement exercée par l’air proportionnelle à la vitesse d’un facteur et opposée au mouvement. On considérera sa vitesse initiale nulle. En appliquant le principe fondamental de la dynamique à l’objet, on obtient une équation différentielle régissant la vitesse de l’objet.
Remarques préliminaires
Sans résoudre analytiquement l’équation différentielle, il est possible de confirmer notre intuition concernant la vitesse limite. En effet, si les frottements équilibrent la gravité, on peut écrire la relation suivante concernant la vitesse d’équilibre :
Cette relation a pour conséquence d’annuler la dérivée :
Une dérivée nulle signifie qu’il n’y a plus d’évolution : la vitesse d’équilibre entre frottements et gravité est aussi la vitesse atteinte à l’état final.
Ce petite calcul montre ainsi qu’en plus d’avoir des informations sur le point de départ (la vitesse initiale ainsi que la pente à l’origine dans notre cas), on en a aussi sur le point d’arrivée (la vitesse finale). Il nous manque juste la transition entre ces deux moments, que l’on peut obtenir approximativement en résolvant l’équation numériquement avec la méthode d’Euler explicite.
Équation de récurrence
On applique la méthode d’Euler pour résoudre l’équation différentielle. Concrètement, cela revient à dire que la solution approchée, la solution numérique, vérifie l’équation obtenue en appliquant l’approximation d’Euler.
On isole à gauche et on transfère le reste dans le membre de droite pour obtenir une relation de récurrence :
On reconnaît une forme similaire à celle de la section précédente, où l’on aurait .
Résolution numérique
On utilise une suite d’instants successifs pour la résolution numérique, et il est courant d’utiliser des pas de temps constants. Cela consiste à choisir les tels que leur écart soit constant et égal à .
On introduit cette notation dans l’équation.
On prendra les valeurs numériques :
- ,
- ,
- et . Cette valeur est acceptable, mais n’offre pas une grande précision, comme nous allons le voir plus loin.
Nous sommes bons pour calculer ! Les ordinateurs font ça très bien, et j’ai écrit à cette fin un court programme Python, qui se trouve dans le bloc masqué ci-dessous. Si vous savez programmer, je vous conseille d’essayer d’écrire votre propre programme avant toute chose, afin de mettre un peu les mains dans le cambouis. Si vous ne savez pas programmer, il est possible d’obtenir un résultat similaire avec un tableur comme Excel. Dans les deux cas, il est intéressant d’avoir un outil pour tester facilement différents paramètres, et ce le sera encore plus dans la partie suivante.
"""
Simulation numérique avec la méthode d'Euler explicite
"""
# Paramètres
t_0 = 0 # Instant initial (s)
y_0 = 0 # Valeur initiale (m/s)
dt = 500e-3 # Pas de temps (s)
t_fin = 10 # Instant final (s)
# Fonction f associée à l'équation différentielle
def f(y, t):
g = 10 # Accélération de la pesanteur (m/s^2)
k_sur_m = 1 # f/m (Hz)
f = g - k_sur_m * y
return f
# Initialisation de la simulation
t_k = t_0
y_k = y_0
# Initialisation des listes pour le stockage du résultat
t = [t_k]
y = [y_k]
# Déroulement de la simulation
while t_k < t_fin:
# Calcul de la solution à l'instant y[k+1]
y_k = y_k + dt * f(y_k, t_k)
# Avancement du temps vers l'instant t[k+1]
t_k = t_k + dt
# Stockage du résultat
t.append(t_k)
y.append(y_k)
# Affichage
print(t)
print(y)
Je consigne les résultats que m’a donnés le programme dans le tableau suivant. Il est redondant afin de bien montrer que le d’une étape devient le de l’étape suivante.
| k | |||
|---|---|---|---|
| 0 | 0,0 s | 0 m/s | 5,0 m/s |
| 1 | 0,5 s | 5,0 m/s | 7,5 m/s |
| 2 | 1,0s | 7,5 m/s | 8,75 m/s |
| 3 | 1,5 s | 8,75 m/s | 9,38 m/s |
| 4 | 2,0 s | 9,38 m/s | 9,69 m/s |
| 5 | 2,5 s | 9,69 m/s | 9,84 m/s |
| 6 | 3,0 s | 9,84 m/s | 9,92 m/s |
| 7 | 3,5 s | 9,92 m/s | 9,96 m/s |
| 8 | 4,0 s | 9,96 m/s | 9,98 m/s |
| 9 | 4,5 s | 9,98 m/s | 9,99 m/s |
Comme on peut s’y attendre, la vitesse atteint une valeur limite de 10 m/s après avoir augmenté progressivement1… Mais à quel point la solution numérique est-elle proche de la réalité ?
Comparaison avec la solution exacte
Il se trouve (comme c’est commode !) que notre équation différentielle admet une solution exacte, qui est la suivante :
On peut voir clairement la solution exacte et la solution numérique sur le graphique suivant.
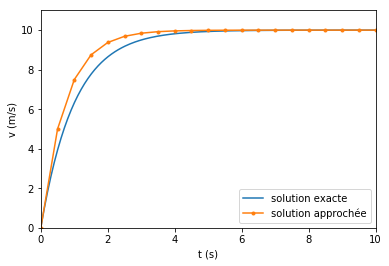
Et le verdict est sans appel : la solution numérique ne colle pas à la solution théorique ! Cela est dû au grand pas de temps que nous avons choisi. Comment alors obtenir une bonne précision ? Réduire le pas est probablement une solution… Nous traitons cette question plus en avant dans l’extrait suivant.
- La limite exacte est effectivement 10 m/s. On peut le démontrer à la physicienne en considérant une solution stationnaire () à l’infini, ou rigoureusement en résolvant formellement l’équation différentielle. Vous pouvez vérifier cela à titre d’exercice !↩
Précision et stabilité
Précision en fonction du pas de temps
Puisque la seule chose imprécise est l’approximation de la dérivée, il faut l’améliorer pour gagner en précision. Sans changer de formule d’approximation, il n’y a pas beaucoup de possibilités : il faut réduire le pas de temps. L’idée est de se rapprocher de la définition formelle de la dérivée, qui est la limite (si elle existe) du taux d’accroissement quand le pas de temps tend vers zéro.
La figure suivante illustre cela sur l’exemple de l’extrait précédent. La réduction du pas de temps permet de s’approcher plus près de la solution exacte, jusqu’à la toucher, en théorie, pour un pas de temps nul. On dira alors que la méthode est convergente. On peut aussi s’intéresser à la vitesse de convergence en fonction du pas de temps : je fournis un lien traitant de ce sujet dans la conclusion.
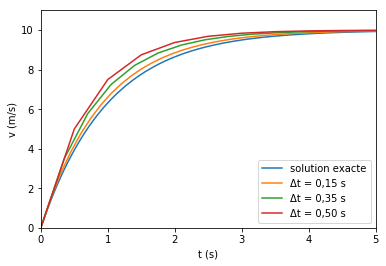
En théorie, faire tendre le pas de temps vers zéro permet d’avoir une précision infinie. En pratique, les nombres à virgule flottante (une approximation des nombres réels) utilisés par les ordinateurs ont une précision finie, et lorsque le pas de temps est minuscule, les erreurs de calcul font perdre en précision. Il y a donc un pas de temps minimal dépendant de la précision des nombres sur la machine effectuant les calculs.
Stabilité en fonction du pas de temps
La méthode d’Euler n’est pas infiniment précise : elle introduit des erreurs d’approximation. Mais une fois qu’une erreur s’est glissée dans le processus, ce qui arrive dès la première étape de calcul, que devient-elle ? Elle peut être soit amplifiée, on parlera de méthode instable, soit au contraire atténuée, et on dira que la méthode est stable.
Dans l’exemple précédent, la solution exacte et la solution numérique se rapprochaient jusqu’à n’être plus discernables à l’œil nu, ce qui signifie que les erreurs s’atténuaient et qu’on était dans un cas stable. Pourtant, la méthode d’Euler n’est pas toujours stable, comme nous allons le voir en analysant plus finement l’exemple.
On note les valeurs prises par la solution exacte de l’équation différentielle. En effectuant un développement limité en 1, on obtient :
où est le terme d’erreur du développement limité2 ; c’est-à-dire la différence entre la valeur exacte de et la somme des deux premiers termes. Ce terme vérifie , c’est-à-dire qu’il est négligeable devant le pas de temps quand celui-ci tend vers zéro. On peut ensuite éliminer la dérivée grâce à l’équation différentielle :
Puisqu’à chaque étape, le calcul se base sur l’étape précédente, les termes d’erreurs du développement limité s’accumulent, et il en résulte une erreur globale d’approximation entre la solution approchée et la solution exacte. À une étape du calcul, on la notera . Nous avons ainsi . À l’étape suivante, l’erreur se propage, et nous avons donc similairement . Dans le schéma d’Euler, on effectue alors les substitutions suivantes :
- on remplace par ,
- et on remplace par .
On obtient alors la relation suivante :
Pour se fixer un peu mieux les idées, les différentes erreurs sont illustrées sur la figure ci-dessous.
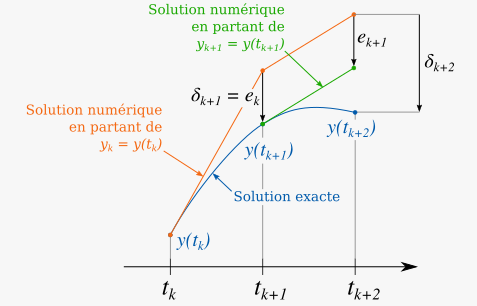
En soustrayant les deux équations précédentes, on obtient l’équation régissant l’erreur d’approximation.
Par simplification, on laisse tomber , tout en conservant l’égalité3.
Il s’agit d’une récurrence géométrique, qu’il est facile d’étudier. Quelles sont les conditions à remplir pour que l’erreur reste bornée et donc que la méthode soit stable ? Il faut que la suite géométrique soit convergente, ce qui se traduit par une condition sur sa raison :
Les variables étant positives, la valeur absolue ne peut pas devenir supérieure à 1, et on ne s’intéresse qu’au cas négatif. Il faut dans ce cas :
En transformant l’inéquation, cela se traduit en condition sur ; il nous faut pour assurer la stabilité :
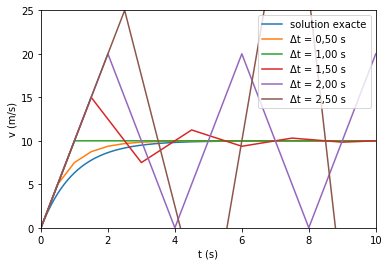
La figure ci-dessous illustre le comportement pour différentes valeurs de .
- Pour un pas de 0,6 seconde, la méthode est stable.
- Pour un pas de 1,5 seconde, la méthode est stable mais présente des oscillations numériques, car est négatif. Ce phénomène est embêtant, car les simulations ne reflètent même plus la réalité de manière qualitative !
- Pour un pas de 2,0 secondes, on se trouve à la limite de stabilité, la solution oscille sans jamais n’être ni amplifiée, ni attenuée.
- Pour un pas de 2,5 secondes, la solution diverge totalement.
- Mathématiquement, il suffit que soit de classe (c’est-à-dire suffisamment lisse) au voisinage de , et d’appliquer la formule de Taylor. Dans le modèle pris pour l’exemple, cette propriété est bien vérifiée par .↩
- C’est aussi ici l’erreur de consistance, c’est-à-dire l’erreur que la méthode d’Euler introduit à l’étape suivante en partant d’une valeur juste. C’est un outil théorique, puisque cette erreur s’introduit dès la première étape de calcul, ce qui fait qu’aucune étape ultérieure ne se fonde sur une valeur exacte. Pire encore, la première valeur est, en général, issue du monde réel et donc déjà entachée d’erreurs de mesure !↩
- Ce n’est pas du tout rigoureux ! On peut cependant raisonnablement supposer que les sont bornés. Dans ce cas-là, si la suite ne diverge pas, elle sera aussi bornée.↩
Vous avez découvert dans ce tutoriel la résolution numérique d’équations différentielles avec la méthode d’Euler explicite.
Sur un exemple, nous avons vu comment augmenter la précision de la méthode en réduisant précautionneusement le pas de temps, et comment un pas de temps trop grand pouvait mener à une instabilité de la résolution numérique. On peut ainsi obtenir un résultat satisfaisant, mais cela n’empêche pas de faire mieux avec d’autres méthodes !
Si vous savez programmer, un bon exercice d’appropriation est d’adapter le petit programme que j’ai donné pour résoudre une autre équation différentielle, et d’observer le comportement de la solution numérique lorsqu’on fait varier les différents paramètres.
Si vous voulez aller voir plus loin, je vous conseille de vous intéresser à un traitement plus mathématique de la méthode d’Euler, qui formalise les intuitions que nous avons eues sur l’exemple. Mais si vous n’aimez pas les mathématiques, passez votre chemin.
Ensuite, rien de tel que d’enchaîner sur les méthodes de Runge-Kutta (avec une approximation plus précise de la dérivée, à pas de temps égal), puis éventuellement sur les méthodes à pas variable (on avance vite quand le signal varie peu et lentement quand il varie rapidement), voire la méthode d’Euler implicite (plus stable, mais nécessite des notions de résolution numérique d’équations non-différentielles).
Illustration du tutoriel : détail d’un portrait d’Euler par Emanuel Handmann, 1753.
Je remercie vivement Vayel, Gabbro, Algue-Rythme, adri1 et Holosmos pour leurs relectures et conseils.

 Pas un mot sur Verlet et Velocity Verlet par contre?
Pas un mot sur Verlet et Velocity Verlet par contre? 

 Merci !
Merci !