Dans ce chapitre, nous allons découvrir ce qu’est Ruby, comment l’installer, et nous ferons une courte introduction à sa syntaxe.
Qu’est-ce que Ruby ?
Avant de nous lancer dans cette grande aventure qu’est l’apprentissage de Ruby, nous devons déjà savoir ce qu’est Ruby.
Pour commencer, Ruby est un langage de programmation.
Mais au fait, qu’est-ce qu’un langage de programmation ?
En lisant ce tutoriel, nous avons une réponse à cette question.
Pour résumer, un langage de programmation est un langage destiné à écrire des programmes informatiques.
Il existe deux grandes catégories de langages :
- avec les langages compilés, le code que nous écrivons passe par un compilateur et ce compilateur génère un exécutable qui peut ensuite être exécuté par notre ordinateur ;
- avec les langages interprétés, le code que nous écrivons doit être lancé dans ce que l’on appelle une machine virtuelle, il n’y a pas d’exécutable de créé.
Ruby est un langage interprété. Nous aurons donc besoin d’une machine virtuelle pour l’exécuter. Sans elle, les programmes ne fonctionneront pas. Cela signifie également que si nous voulons distribuer un programme écrit en Ruby, il faudra que les personnes qui utilisent notre programme aient cette machine virtuelle d’installée (cette machine virtuelle est en fait Ruby). Ils devront donc télécharger et installer Ruby (ou nous devrons distribuer Ruby avec notre programme).
Cette distribution est possible parce que Ruby est également un langage (et un logiciel) libre. Nous n’allons pas être longs sur ce point (pour plus d’informations, voir la licence GPL), mais retenons en gros que nous pouvons utiliser et redistribuer Ruby gratuitement et même créer des programmes payants avec.
Ruby est un langage complet et permet de faire beaucoup de choses (on peut par exemple travailler sur un site Web en utilisant Ruby On Rails). De plus, il permet de faire les choses de plusieurs manières différentes. C’est l’une de ses forces, mais paradoxalement, c’est aussi l’une des choses qui lui sont parfois reprochées : on peut faire les choses de plusieurs manières différentes, quelle méthode faut-il alors utiliser ?
En tout cas, il reste un langage pratique, facile à utiliser et il est même portable. Nous pourrons donc l’utiliser sur différents systèmes.
Installation
Avant de coder en Ruby, il va de soi qu’il faut l’installer. Heureusement, nous allons voir pas à pas comment faire.
Il y a plusieurs façons d’installer Ruby. Elles sont détaillées sur cette page. Nous allons voir la méthode la plus simple.
Installation sous Windows
Pour commencer, téléchargeons la dernière version de RubyInstaller sur cette page.
Ensuite, il nous suffit d’exécuter l’installateur téléchargé.
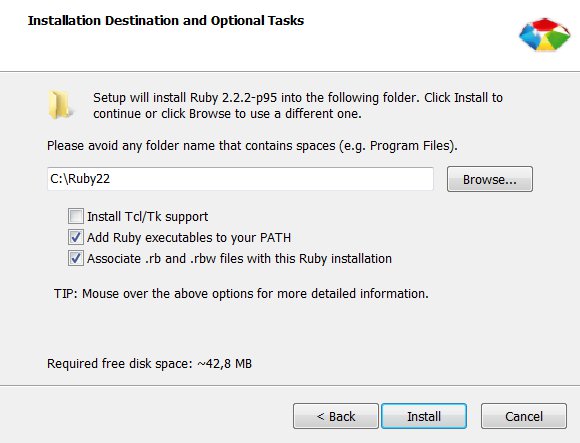
Il nous faut cliquer sur « Suivant » → « Suivant » → « Installer » en prenant soin de cocher les cases comme ci-dessous.
Pour vérifier que Ruby est bien installé, nous pouvons utiliser la console. Ouvrons l’application « Invite de commande » et tapons ruby -v avant de valider en appuyant sur Entrée. Nous sommes censés obtenir le numéro de la version de Ruby qui est installée.
Notons quand même que bien que Ruby soit multi-plateforme, Linux est particulièrement adapté à son utilisation, bien plus que Windows.
Installation sous Linux
Ruby est déjà installé sur certaines distributions. Pour savoir s’il est déjà installé, nous pouvons utiliser la commande ruby. Pour cela, il faut ouvrir un terminal (généralement le terminal est l’application « Konsole » ou encore « Terminal »). Après l’avoir ouvert, tapons ruby avant de valider en appuyant sur Entrée.
Si la commande ne renvoie pas d’erreur, alors Ruby est installé (Notons également la commande ruby -v qui renvoie le numéro de version).
Si Ruby n’est pas encore installé, le plus simple est d’utiliser notre gestionnaire de paquets pour l’installer. Nous pouvons utiliser un gestionnaire de paquets graphiques ou en ligne de commandes au choix.
$ sudo apt-get install ruby-full # Sous Ubuntu, Linux Mint, Debian, etc.
$ sudo pacman -S ruby # Sous Arch Linux.
Installation sous OS X
Nous avons de la chance, depuis quelques versions, Ruby est installé de base sur OS X. Nous n’avons donc rien à faire.
Lançons quand même la commande ruby -v dans notre terminal pour connaître la version qui est installée. Pour cela, ouvrons le terminal (il s’agit de l’application « Terminal.App »), tapons ruby -v et validons en appuyant sur Entrée. Nous obtenons le numéro de la version de Ruby qui est installée.
Ruby est maintenant installé sur notre ordinateur. Il nous faut maintenant apprendre à l’utiliser.
Prise en main
IRB
Ruby possède ce que l’on appelle un environnement interactif, ici appelé IRB.
IRB interprète notre code au fur et à mesure que nous l’écrivons : nous entrons une instruction et nous appuyons sur Entrée, cette instruction est alors exécutée.
Pour lancer IRB, il faut passer par la ligne de commande que nous avons déjà utilisée précédemment. Il s’agit de l’application « Invite de commande » sous Windows et de « Terminal.app » sous OS X. Une fois l’invite de commande ouverte, il faut taper irb. Nous avons maintenant une magnifique console qui interprète ce que nous écrivons en Ruby.
En lançant IRB, nous nous retrouvons face au symbole >. Ce chevron signifie une chose : IRB est à nos ordres, il attend nos instructions. Lorsqu’il nous « répond », sa réponse est située après le signe => sur une nouvelle ligne. Par exemple, en tapant 2 il répond 2 (oui, il répond bien 2).
> 2
=> 2
En Ruby, les instructions sont séparées par un point-virgule. Celui-ci peut cependant être omis s’il n’y a qu’une instruction par ligne.
Ainsi, nous pouvons écrire cela.
3; 2
Mais ceci ne fonctionnera pas et nous donnera une belle erreur.
3 4
Nous conseillons alors de ne mettre qu’une seule instruction par ligne.
Pour quitter IRB, nous devons entrer quit et valider.
Opérations mathématiques
Les premières instructions que nous allons voir sont les opérations mathématiques. IRB fonctionne comme une calculatrice et nous donne le résultat à la ligne juste en dessous. Il respecte même les priorités (avec ou sans parenthèses). Essayons d’écrire des opérations mathématiques. Nous obtenons quelque chose de ce genre.
> 3 + 2
=> 5
> 2 * 3 + 5
=> 11
> (2 * 3) + 5
=> 11
> (6 - 2)*(8 + 25)
=> 132
Nous pouvons même assigner des valeurs à une lettre pour effectuer des opérations sur celle-ci.
> x = 4
=> 4
> y = 7
=> 7
> x + y
=> 11
Il faut faire attention aux divisions. L’invite donne toujours un résultat entier : par exemple, 5 / 3 = 1.
Nous allons voir quel est le problème de la division. Mais avant cela, voici un tableau des opérations mathématiques que nous avons vues.
| Action | Code | Affichage |
|---|---|---|
| Additionner | 3 + 2 |
Affiche 5. |
| Soustraire | 3 - 2 |
Affiche 1. |
| Multiplier | 3 * 2 |
Affiche 6. |
| Diviser | 3 / 2 |
Affiche 1. |
| Modulo | 3 % 2 |
Affiche 1 (le reste de la division euclidienne). |
Nous pouvons également y ajouter l’opération puissance qui s’utilise avec **. En tapant 2 ** 2, on obtient donc 4.
Un peu de sucre syntaxique
L’expression sucre syntaxique désigne des parties d’un langage de programmation qui permettent d’écrire et de lire du code plus facilement. À ce niveau du cours, nous n’avons pas encore de quoi voir du sucre syntaxique, mais il existe des raccourcis aux opérateurs mathématiques que l’on peut considérer comme du sucre syntaxique.
Prenons l’exemple d’une variable variable qui vaut 4. On veut la multiplier par 3. Le code qui s’impose est le suivant.
variable = 4
variable = variable * 3
Ceci est parfaitement correct. Cependant, on peut raccourcir cette écriture en écrivant ceci.
variable = 4
variable *= 3
Et cette syntaxe ne marche pas que pour la multiplication. Voici un tableau des opérations et de leurs équivalents.
Opération | Équivalent |
|---|---|
|
|
|
|
|
|
|
|
|
|
Notons de plus que nous pouvons utiliser le symbole _ dans nos nombres. Ainsi, 12_3_2 et 1232 sont les mêmes nombres. Ceci nous permet de regrouper certains chiffres, donc d’avoir une meilleure lisibilité. Par exemple, 10_000_000 est beaucoup plus lisible que 10000000.
Nous avons également la possibilité de noter les nombres en binaire (grâce au préfixe 0b), en octal (grâce aux préfixes 0 et 0o) et en hexadécimal (grâce au préfixe 0x). En fait, il y a aussi le préfixe 0d pour écrire les nombres en décimal.
> 10 => 10
> 0d10 => 10
> 0b10 => 2
> 010 => 8
> 0o10 => 8
> 0x10 => 16
> 0xab => 171
Nous pouvons écrire les lettres des préfixes en majuscule ou en minuscule. De même, Ruby n’est pas sensible à la casse pour la notation hexadécimale. Ainsi, 0B10 et 0b10 sont équivalents, de même que 0xAb1 et 0XAB1.
Entiers et flottants
En voyant ce que sont les entiers et les flottants, nous verrons qu’en fait, le résultat que nous obtenons avec la division n’est pas une erreur.
On appelle un entier un nombre comme 3, 37 ou -12. Un flottant est un nombre avec une partie décimale comme 5, 6 ou 32,5.
Notre problème est directement lié aux notions d’entiers et de flottants : en fait, quand on tape 3 / 2, on divise deux entiers. Le résultat est donc aussi un entier. En toute logique, pour obtenir un résultat à virgule (donc un flottant), il faut diviser deux flottants. Donc pour obtenir le résultat attendu, il nous aurait fallu taper 3.0 / 2.0. Entrons 3.0 / 2.0 dans IRB, et admirons le résultat.
Nous n’avons pas pu le manquer. Pour écrire un nombre décimal, on utilise la notation anglo-saxonne. Il faut donc utiliser un point et non une virgule ! De plus, nous sommes obligés de rajouter la partie décimale même si elle est nulle pour préciser qu’on utilise un flottant.
Lorsque nous additionnons un entier et un flottant, nous obtenons un flottant. Ainsi, en tapant 2 + 3.5, on obtient bien 5.5. La conversion est faite implicitement.
Notons que nous pouvons utiliser la notation E pour les puissances de 10 (là encore, la casse n’a pas d’importance). Ainsi, 12e2 vaut 1200 et 1.2E-2 vaut 0.012.
Il nous faut faire des essais, regarder les résultats des calculs et nous habituer à les utiliser. Nous en aurons besoin au prochain chapitre !
Exercices
Faisons quelques exercices avant de passer au chapitre suivant. Voyons si la notion de flottants est bien comprise. Nous allons donner quelques calculs. Le but de l’exercice est de deviner le résultat, avant de l’exécuter pour vérifier le résultat. Simple, non ?
Commençons :
2 + 3;3.2 + 4;4 / 3;4 / 3.0;4,0 / 3,0.
Jusque là, il n’y a que de petits calculs. Passons à d’autres choses :
4.0 % 2.4;5 * (2 + 5);3 + 2 * (2 + 5));3(2 + 2) * 3.
Correction :
2 + 3donne5comme résultat (c’est une addition de deux entiers) ;3.2 + 4donne7.2;4 / 3donne1(c’est une division entre entiers le résultat est donc un entier) ;4 / 3.0donne1.3333(lorsque l’on fait une opération entre un entier et un flottant, le résultat est un flottant) ;4,0 / 3,0donne une erreur car le séparateur décimal est le point et non la virgule.
Et pour les autres :
4.0 % 2.4donne étonnement1.6. Le reste est calculé pour une division de flottants quand avec d’autres langages on obtiendrait une erreur ;5 * (2 + 5)donne35: le calcul entre parenthèses est effectué avant la multiplication. Le calcul effectué est donc5 * 7;3 + 2 * (2 + 5))donne une erreur : une des parenthèses n’est pas ouverte ;3(2 + 2) * 3donne aussi une erreur : nous ne pouvons pas ne pas écrire de signes, le*doit être précisé.
Nous avons maintenant tous les outils pour nous lancer dans la programmation en Ruby. Pour le moment, nous n’avons rien fait d’extraordinaire, mais c’est quand même une base à avoir, et il ne faut pas oublier de nous entraîner.
- On peut exécuter des instructions via IRB, qui interprète le code Ruby que nous écrivons.
- Ruby nous permet de faire des opérations mathématiques élémentaires (addition, soustraction, multiplication, division) mais aussi le modulo (reste de la division euclidienne) et la puissance.
- Les nombres peuvent être notés de plusieurs manières (plusieurs bases sont disponibles, l’écriture scientifique est disponible, etc.).
- On n’utilise pas la virgule mais le point comme séparateur décimal.
- Les entiers sont à différencier des flottants (notamment une division d’entiers donne un entier) même si les entiers sont automatiquement convertis en flottants lors d’une opération avec un flottant.