Les variables et les opérateurs

• Installer les outils de développement
• Sommaire
• Lire les entrées clavier

Nous commençons maintenant sérieusement la programmation. Dans ce chapitre, nous allons découvrir les variables. On les retrouve dans la quasi-totalité des langages de programmation. Une variable est un élément qui stocke des informations de toute sorte en mémoire : des chiffres, des résultats de calcul, des tableaux, des renseignements fournis par l'utilisateur…

Vous ne pourrez pas programmer sans variables. Il est donc indispensable que je vous les présente !

• Petit rappel
• Les différents types de variables
• Les opérateurs arithmétiques
• Les conversions, ou « cast »
• Depuis Java 7 : le formatage des nombres

Petit rappel

Avant de commencer, je vous propose un petit rappel sur le fonctionnement d'un ordinateur et particulièrement sur la façon dont ce dernier interprète notre façon de voir le monde…

Vous n'êtes pas sans savoir que votre ordinateur ne parle qu'une seule langue : le binaire ! Le langage binaire est une simple suite de 0 et de 1. Vous devez vous rendre compte qu'il nous serait très difficile, en tant qu'êtres humains, d'écrire des programmes informatiques pour expliquer à nos ordinateurs ce qu'ils doivent faire, entièrement en binaire… Vous imaginez ! Des millions de 0 et de 1 qui se suivent ! Non, ce n'était pas possible ! De ce fait, des langages de programmation ont été créés afin que nous ayons à disposition des instructions claires pour créer nos programmes. Ces programmes sont ensuite compilés pour que nos instructions humainement compréhensibles soient, après coup, compréhensible par votre machine.

Le langage binaire est donc une suite de 0 et de 1 qu'on appelle bit. Si vous êtes habitués à la manipulation de fichiers (audio, vidéos, etc.) vous devez savoir qu'il existe plusieurs catégories de poids de programme (Ko, Mo, Go, etc.). Tous ces poids correspondent au système métrique informatique. Le tableau suivant présente les poids les plus fréquemment rencontrés :

Si vous vous posez cette question c'est parce que vous ne savez pas encore compter comme un ordinateur et que vous êtes trop habitués à utiliser un système en base 10. Je sais, c'est un peu confus… Pour comprendre pourquoi ce découpage est fait de la sorte, vous devez comprendre que votre façon de compter n'est pas identique à celle de votre machine. En effet, vous avez l'habitude de compter ainsi :

1

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 ... 254, 255, 256 ... 12345678, 12345679, 12345680

Cette façon de compter repose sur une base 10, car elle se décompose en utilisant des puissances de 10. Ainsi, le nombre 1024 peut se décomposer de cette façon : $1*1000 + 0*100 + 2*10 + 4*1$

Pour bien comprendre ce qui suit, vous devez aussi savoir que tout nombre élevé à la puissance 0 vaut 1, donc $10^0 = 1$. Partant de ce postulat, nous pouvons donc réécrire la décomposition du nombre 1024 ainsi : $1*10^3 + 0*10^2 + 2*10^1 + 4*10^0$. Nous multiplions donc la base utilisée, ordonnée par puissance, par un nombre compris entre 0 et cette base moins 1 (de 0 à 9).

Sauf que votre machine parle en binaire, elle compte donc en base 2. Cela revient donc à appliquer la décomposition précédente en remplaçant les 10 par des 2. Par contre, vous n'aurez que deux multiplicateurs possibles : 0 ou 1 (et oui, vous êtes en base 2). De ce fait, en base 2, nous pourrions avoir ce genre de chose : $1*2^3 + 1*2^2 + 0*2^1 + 1*2^0$, qui peut se traduire de la sorte : $1*8 + 1*4 + 0*2 + 1*1$ donc $8 + 4 + 0 + 1$ soit $13$.

Donc, 1101 en base 2 s'écrit 13 en base 10. Et donc pourquoi des paquets de 1024 comme délimiteur de poids ? Car ce nombre correspond à une puissance de 2 : $1024 = 2^1^0$.

Dans le monde de l'informatique, il existe une autre façon de compter très répandue : l'hexadécimal. Dans ce cas, nous comptons en base 16 :

1

1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 1A, 1B, 1C.... 5E, 5F, 60, ... A53A, A53B, A53C...

Le côté pratique de cette notation c'est qu'elle se base sur une subdivision d'un octet. Pour représenter un nombre de 0 à 15 (donc les seize premiers nombres), 4 bits sont nécessaires : $0*2^3 + 0*2^2 + 0*2^1 + 0*2^0 = 0$ et $1*2^3 + 1*2^2 + 1*2^1 + 1*2^0 = 15$. En fait, vous savez maintenant qu'un octet est un regroupement de 8 bits. Utiliser l'hexadécimal permet de simplifier la notation binaire car, si vous regroupez votre octet de bits en deux paquets de 4 bits, vous pouvez représenter chaque paquet avec un caractère hexadécimal. Voici un exemple :

1
2
3
4

10110100 -> 1011 0100
1011 (en base 2) = 11 (base 10) = B (en base 16)
0100 (en base 2) = 4 (base 10) = 4 (en base 16)
Donc 10110100 -> 1011 0100 -> B4

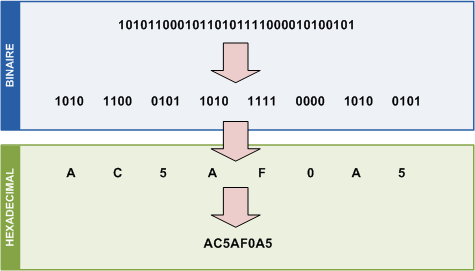
La figure suivante représente un nombre binaire plus conséquent :

Les différents types de variables

Nous allons commencer par découvrir comment créer des variables dans la mémoire. Pour cela, il faut les déclarer. Une déclaration de variable se fait comme ceci :

1

<Type de la variable> <Nom de la variable> ;

Cette opération se termine toujours par un point-virgule « ; » (comme toutes les instructions de ce langage). Ensuite, on l'initialise en entrant une valeur.

En Java, nous avons deux types de variables :

1. des variables de type simple ou « primitif » ;
2. des variables de type complexe ou des « objets ».

Ce qu'on appelle des types simples ou types primitifs, en Java, ce sont tout bonnement des nombres entiers, des nombres réels, des booléens ou encore des caractères, et vous allez voir qu'il y a plusieurs façons de déclarer certains de ces types.

Les variables de type numérique

Le type byte (1 octet) peut contenir les entiers entre -128 et +127.

1
2

byte temperature;
temperature = 64;

Le type short (2 octets) contient les entiers compris entre -32768 et +32767.

1
2

short vitesseMax;
vitesseMax = 32000;

Le type int (4 octets) va de -210⁹ à 210⁹ (2 et 9 zéros derrière… ce qui fait déjà un joli nombre).

1
2

int temperatureSoleil;
temperatureSoleil = 15600000; //La température est exprimée en kelvins

Le type long (8 octets) peut aller de $-9*10^{18}$ à $9*10^{18}$ (encore plus gros…).

1
2

long anneeLumiere;
anneeLumiere = 9460700000000000L;

Le type float (4 octets) est utilisé pour les nombres avec une virgule flottante.

1
2

float pi;
pi = 3.141592653f;

Ou encore :

1
2

float nombre;
nombre = 2.0f;

Le type double (8 octets) est identique à float, si ce n'est qu'il contient plus de chiffres derrière la virgule et qu'il n'a pas de suffixe.

1
2

double division;
division = 0.333333333333333333333333333333333333333333334d;

Des variables stockant un caractère

Le type char contient un caractère stocké entre apostrophes (« ' ' »), comme ceci :

1
2

char caractere;
caractere = 'A';

Des variables de type booléen

Le type boolean, lui, ne peut contenir que deux valeurs  : true (vrai) ou false (faux), sans guillemets (ces valeurs sont natives dans le langage, il les comprend directement et sait les interpréter).

1
2

boolean question;
question = true;

Et aussi le type String

Le type String permet de gérer les chaînes de caractères, c'est-à-dire le stockage de texte.

Il s'agit d'une variable d'un type plus complexe que l'on appelle objet. Vous verrez que celle-ci s'utilise un peu différemment des variables précédentes :

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

//Première méthode de déclaration
String phrase;
phrase = "Titi et Grosminet";

//Deuxième méthode de déclaration
String str = new String();
str = "Une autre chaîne de caractères";

//Troisième méthode de déclaration
String string = "Une autre chaîne";

//Quatrième méthode de déclaration
String chaine = new String("Et une de plus !");

Cela a été mentionné plus haut : String n'est pas un type de variable, mais un objet. Notre variable est un objet, on parle aussi d'une instance : ici, une instance de la classe String. Nous y reviendrons lorsque nous aborderons les objets.

C'est simple : il s'agit d'une convention de nommage. En fait, c'est une façon d'appeler nos classes, nos variables, etc. Il faut que vous essayiez de la respecter au maximum. Cette convention, la voici :

• tous vos noms de classes doivent commencer par une majuscule ;
• tous vos noms de variables doivent commencer par une minuscule ;
• si le nom d'une variable est composé de plusieurs mots, le premier commence par une minuscule, le ou les autres par une majuscule, et ce, sans séparation ;
• tout ceci sans accentuation !

Je sais que la première classe que je vous ai demandé de créer ne respecte pas cette convention, mais je ne voulais pas vous en parler à ce moment-là… Donc, à présent, je vous demanderai de ne pas oublier ces règles !

Voici quelques exemples de noms de classes et de variables :

1
2
3
4
5
6
7

public class Toto{}
public class Nombre{}
public class TotoEtTiti{}
String chaine;
String chaineDeCaracteres;
int nombre;
int nombrePlusGrand;

Donc, pour en revenir au pourquoi du comment, je vous ai dit que les variables de type String sont des objets. Les objets sont définis par une ossature (un squelette) qui est en fait une classe. Ici, nous utilisons un objet String défini par une classe qui s'appelle « String » ; c'est pourquoi String a une majuscule et pas int, float, etc., qui eux ne sont pas définis par une classe.

Faites donc bien attention lors de vos déclarations de variables… Une petite astuce quand même (enfin deux, plutôt) : on peut très bien compacter les phases de déclaration et d'initialisation en une seule phase ! Comme ceci :

1
2
3
4

int entier = 32;
float pi = 3.1416f;
char carac = 'z';
String mot = new String("Coucou");

Et lorsque nous avons plusieurs variables d'un même type, nous pouvons résumer tout ceci à une déclaration :

1

int nbre1 = 2, nbre2 = 3, nbre3 = 0;

Ici, toutes les variables sont des entiers, et toutes sont initialisées.

Avant de nous lancer dans la programmation, nous allons faire un peu de mathématiques avec nos variables.

Les opérateurs arithmétiques

Les opérateurs arithmétiques sont ceux que l'on apprend à l'école primaire… ou presque :

• « + » : permet d'additionner deux variables numériques (mais aussi de concaténer des chaînes de caractères ; ne vous inquiétez pas, on aura l'occasion d'y revenir).
• « - » : permet de soustraire deux variables numériques.
• « * » : permet de multiplier deux variables numériques.
• « / » : permet de diviser deux variables numériques (mais je crois que vous aviez deviné).
• « % » : permet de renvoyer le reste de la division entière de deux variables de type numérique ; cet opérateur s'appelle le modulo.

Quelques exemples de calcul

1
2
3
4
5
6
7
8

int nbre1, nbre2, nbre3;  //Déclaration des variables

nbre1 = 1 + 3;            //nbre1 vaut 4
nbre2 = 2 * 6;            //nbre2 vaut 12
nbre3 = nbre2 / nbre1;    //nbre3 vaut 3
nbre1 = 5 % 2;            //nbre1 vaut 1, car 5 = 2 * 2 + 1
nbre2 = 99 % 8;           //nbre2 vaut 3, car 99 = 8 * 12 + 3
nbre3 = 6 % 3;            //là, nbre3 vaut 0, car il n'y a pas de reste

Ici, nous voyons bien que nous pouvons affecter des résultats d'opérations sur des nombres à nos variables, mais aussi affecter des résultats d'opérations sur des variables de même type.

Maintenant, voici quelque chose que les personnes qui n'ont jamais programmé ont du mal à intégrer. Je garde la même déclaration de variables que ci-dessus.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

int nbre1, nbre2, nbre3;    //Déclaration des variables
nbre1 = nbre2 = nbre3 = 0;  //Initialisation

nbre1 = nbre1 + 1;     //nbre1 = lui-même, donc 0 + 1 => nbre1 = 1
nbre1 = nbre1 + 1;     //nbre1 = 1 (cf. ci-dessus), maintenant, nbre1 = 1 + 1 = 2
nbre2 = nbre1;         //nbre2 = nbre1 = 2
nbre2 = nbre2 * 2;     //nbre2 = 2 => nbre2 = 2 * 2 = 4
nbre3 = nbre2;         //nbre3 = nbre2 = 4
nbre3 = nbre3 / nbre3; //nbre3 = 4 / 4 = 1
nbre1 = nbre3;         //nbre1 = nbre3 = 1
nbre1 = nbre1 - 1;     //nbre1 = 1 - 1 = 0

Et là aussi, il existe une syntaxe qui raccourcit l'écriture de ce genre d'opérations. Regardez bien :

1
2
3
4

nbre1 = nbre1 + 1;
nbre1 += 1;
nbre1++;
++nbre1;

Les trois premières syntaxes correspondent exactement à la même opération. La troisième sera certainement celle que vous utiliserez le plus, mais elle ne fonctionne que pour augmenter d'une unité la valeur de nbre1 ! Si vous voulez augmenter de 2 la valeur d'une variable, utilisez les deux syntaxes précédentes. On appelle cela l'incrémentation. La dernière fait la même chose que la troisième, mais il y a une subtilité dont nous reparlerons dans le chapitre sur les boucles.

Pour la soustraction, la syntaxe est identique :

1
2
3
4

nbre1 = nbre1 - 1;
nbre1 -= 1;
nbre1--;
--nbre1;

Même commentaire que pour l'addition, sauf qu'ici, la troisième syntaxe s'appelle la décrémentation.

Les raccourcis pour la multiplication fonctionnent de la même manière ; regardez plutôt :

1
2
3
4

nbre1 = nbre1 * 2;
nbre1 *= 2;
nbre1 = nbre1 / 2;
nbre1 /= 2;

Voici les raisons de ma mise en garde : comme je vous l'ai dit précédemment, chaque type de variable a une capacité différente et, pour faire simple, nous allons comparer nos variables à différents récipients. Une variable de type :

• byte correspondrait à un dé à coudre, elle ne peut pas contenir grand-chose ;
• int serait un verre, c'est déjà plus grand ;
• double serait un baril. Pfiou, on en met là-dedans

À partir de là, ce n'est plus qu'une question de bon sens. Vous devez facilement constater qu'il est possible de mettre le contenu d'un dé à coudre dans un verre ou un baril. Par contre, si vous versez le contenu d'un baril dans un verre… il y en a plein par terre ! Ainsi, si nous affectons le résultat d'une opération sur deux variables de type double dans une variable de type int, le résultat sera de type int et ne sera donc pas un réel mais un entier.

Pour afficher le contenu d'une variable dans la console, appelez l'instruction System.out.println(maVariable);, ou encore System.out.print(maVariable);.

Je suppose que vous voudriez aussi mettre du texte en même temps que vos variables… Eh bien sachez que l'opérateur « + » sert aussi d'opérateur de concaténation, c'est-à-dire qu'il permet de mélanger du texte brut et des variables. Voici un exemple d'affichage avec une perte de précision :

1
2
3

double nbre1 = 10, nbre2 = 3;
int resultat = (int)(nbre1 / nbre2);
System.out.println("Le résultat est = " + resultat);

Cependant, pour le bien de ce chapitre, nous n'allons pas utiliser cette méthode. Vous allez constater que le résultat affiché est 3 au lieu de 3.33333333333333… Et je pense que ceci vous intrigue :

1

int resultat = (int)(nbre1 / nbre2);

Avant que je ne vous explique, remplacez la ligne citée précédemment par :

1

int resultat = nbre1 / nbre2;

Vous allez voir qu'Eclipse n'aime pas du tout ! Pour comprendre cela, nous allons voir les conversions.

Les conversions, ou « cast »

Comme expliqué précédemment, les variables de type double contiennent plus d'informations que les variables de type int. Ici, il va falloir écouter comme il faut… heu, pardon : lire comme il faut ! Nous allons voir un truc super important en Java. Ne vous en déplaise, vous serez amenés à convertir des variables.

D'un type int en type float :

1
2

int i = 123;
float j = (float)i;

D'un type int en double :

1
2

int i = 123;
double j = (double)i;

Et inversement :

1
2
3
4

double i = 1.23;
double j = 2.9999999;
int k = (int)i;        //k vaut 1
k = (int)j;            //k vaut 2

Ce type de conversion s'appelle une « conversion d'ajustement », ou cast de variable.

Vous l'avez vu : nous pouvons passer directement d'un type int à un type double. L'inverse, cependant, ne se déroulera pas sans une perte de précision. En effet, comme vous avez pu le constater, lorsque nous castons un double en int, la valeur de ce double est tronquée, ce qui signifie que l'int en question ne prendra que la valeur entière du double, quelle que soit celle des décimales.

Pour en revenir à notre problème de tout à l’heure, il est aussi possible de caster le résultat d'une opération mathématique en la mettant entre « ( ) » et en la précédant du type de cast souhaité. Donc :

1
2
3

double nbre1 = 10, nbre2 = 3;
int resultat = (int)(nbre1 / nbre2);
System.out.println("Le résultat est = " + resultat);

Voilà qui fonctionne parfaitement. Pour bien faire, vous devriez mettre le résultat de l'opération en type double. Et si on fait l'inverse : si nous déclarons deux entiers et que nous mettons le résultat dans un double ? Voici une possibilité :

1
2
3

int nbre1 = 3, nbre2 = 2;
double resultat = nbre1 / nbre2;
System.out.println("Le résultat est = " + resultat);

Vous aurez « 1 » comme résultat. Je ne caste pas ici, car un double peut contenir un int.

En voici une autre :

1
2
3

int nbre1 = 3, nbre2 = 2;
double resultat = (double)(nbre1 / nbre2);
System.out.println("Le résultat est = " + resultat);

Idem… Afin de comprendre pourquoi, vous devez savoir qu'en Java, comme dans d'autres langages d'ailleurs, il y a la notion de priorité d'opération ; et là, nous en avons un très bon exemple !

Dans le cas qui nous intéresse, il y a trois opérations :

• un calcul ;
• un cast sur le résultat de l'opération ;
• une affectation dans la variable resultat.

Eh bien, Java exécute notre ligne dans cet ordre ! Il fait le calcul (ici $3/2$), il caste le résultat en double, puis il l'affecte dans notre variable resultat.

Vous vous demandez sûrement pourquoi vous n'avez pas 1.5… C'est simple : lors de la première opération de Java, la JVM voit un cast à effectuer, mais sur un résultat de calcul. La JVM fait ce calcul (division de deux int qui, ici, nous donne 1), puis le cast (toujours 1), et affecte la valeur à la variable (encore et toujours 1). Donc, pour avoir un résultat correct, il faudrait caster chaque nombre avant de faire l'opération, comme ceci :

1
2
3
4

int nbre1 = 3, nbre2 = 2;
double resultat = (double)(nbre1) / (double)(nbre2);
System.out.println("Le résultat est = " + resultat); 
//affiche : Le résultat est = 1.5

Je ne vais pas trop détailler ce qui suit (vous verrez cela plus en détail dans la partie sur la programmation orientée objet) ; mais vous allez maintenant apprendre à transformer l'argument d'un type donné, int par exemple, en String.

1
2
3

int i = 12;
String j = new String();
j = j.valueOf(i);

j est donc une variable de type String contenant la chaîne de caractères 12. Sachez que ceci fonctionne aussi avec les autres types numériques. Voyons maintenant comment faire marche arrière en partant de ce que nous venons de faire.

1
2
3
4

int i = 12;
String j = new String();
j = j.valueOf(i);
int k = Integer.valueOf(j).intValue();

Maintenant, la variable k de type int contient le nombre « 12 ».

Depuis Java 7 : le formatage des nombres

Comme vous le savez sûrement, le langage Java est en perpétuelle évolution. Les concepteurs ne cessent d'ajouter de nouvelles fonctionnalités qui simplifient la vie des développeurs. Ainsi dans la version 7 de Java, vous avez la possibilité de formater vos variables de types numériques avec un séparateur, l'underscore (_), ce qui peut s'avérer très pratique pour de grands nombres qui peuvent être difficiles à lire. Voici quelques exemples :

1
2
3
4
5
6
7
8
9

double nombre = 1000000000000d; // cast en d
//Peut s'écrire ainsi
double nombre = 1____000____000___000_000d; // cast en d
//Le nombre d'underscore n'a pas d'importance

//Voici quelques autres exemple d'utilisation
int entier = 32_000;
double monDouble = 12_34_56_78_89_10d; // cast en d
double monDouble2 = 1234_5678_8910d;   // cast en d

Les underscore doivent être placés entre deux caractères numériques : ils ne peuvent donc pas être utilisés en début ou en fin de déclaration ni avant ou après un séparateur de décimal. Ainsi, ces déclarations ne sont pas valides :

1
2
3

double d = 123_.159;
int entier = _123;
int entier2 = 123_;

Avant Java 7, il était possible de déclarer des expressions numériques en hexadécimal, en utilisant le préfixe « 0x » :

1
2
3

int entier = 255; //Peut s'écrire « int entier = 0xFF; »
int entier = 20; //Peut s'écrire « int entier = 0x14; »
int entier = 5112; //Peut s'écrire « int entier = 0x13_F8; »

Depuis java 7, vous avez aussi la possibilité d'utiliser la notation binaire, en utilisant le préfixe « 0b » :

1
2
3

int entier = 0b1111_1111; //Est équivalent à : « int entier = 255; »
int entier = 0b1000_0000_0000; //Est équivalent à : « int entier = 2048; »
int entier = 0b100000000000; //Est équivalent à : « int entier = 2048; »

Certains programmes Java travaillent directement sur les bits, il peut donc être plus pratique de les représenter ainsi avant de les manipuler.

• Les variables sont essentielles dans la construction de programmes informatiques.
• On affecte une valeur dans une variable avec l'opérateur égal (« = »).
• Après avoir affecté une valeur à une variable, l'instruction doit se terminer par un point-virgule (« ; »).
• Vos noms de variables ne doivent contenir ni caractères accentués ni espaces et doivent, dans la mesure du possible, respecter la convention de nommage Java.
• Lorsque vous effectuez des opérations sur des variables, prenez garde à leur type : vous pourriez perdre en précision.
• Vous pouvez caster un résultat en ajoutant un type devant celui-ci : (int), (double), etc.
• Prenez garde aux priorités lorsque vous castez le résultat d'opérations, faute de quoi ce dernier risque d'être incorrect.

• Installer les outils de développement
• Sommaire
• Lire les entrées clavier