Dans cette partie, nous allons voir le principe de l’algorithme ID3 à l’aide d’un exemple. Ensuite je vous donnerai le pseudo-code afin de nous lancer dans une implémentation en Python3.
L'algorithme ID3
C’est, pour commencer, cet algorithme qui va être expliqué. ID3 veut dire Iterative Dichotomiser 3. Il va être expliqué à l’aide d’un premier exemple, puis l’algorithme sera explicité, et enfin quelques améliorations possibles seront expliquées.
1. Exemple de playTennis
Voici l’exemple utilisé par Quinlan en personne pour expliquer son algorithme dans le magazine Machine Learning. L’algorithme ID3 part d’un tableau (de manière plus générale, d’un set, ensemble en anglais) d’exemples étiquetés duquel va découler un arbre qui pourra prédire les étiquettes de nouveaux exemples non étiquetés donnés par après.
Comme vous pouvez le voir, ID3 est bien un algorithme d’apprentissage automatique vu qu’il est bien question d’exemples, d’étiquettes, d’attributs, de classification, etc. et c’est bien un arbre de décision parce que… parce que c’est un arbre pardi ! 
1.1. Tableau de valeurs
Voici le tableau contenant les informations nécessaires à l’explication de l’algorithme tel qu’expliqué par Ross Quinlan.
|
Jour |
Attributs des exemples |
Classe |
|||
|---|---|---|---|---|---|
|
Prévisions |
Température |
Humidité |
Vent |
||
|
1 |
Ensoleillé |
Chaud |
Élevée |
Faible |
Non |
|
2 |
Ensoleillé |
Chaud |
Élevée |
Fort |
Non |
|
3 |
Nuageux |
Chaud |
Élevée |
Faible |
Oui |
|
4 |
Pluvieux |
Moyen |
Élevée |
Faible |
Oui |
|
5 |
Pluvieux |
Frais |
Normale |
Faible |
Oui |
|
6 |
Pluvieux |
Frais |
Normale |
Fort |
Non |
|
7 |
Nuageux |
Frais |
Normale |
Fort |
Oui |
|
8 |
Ensoleillé |
Moyen |
Élevée |
Faible |
Non |
|
9 |
Ensoleillé |
Frais |
Normale |
Faible |
Oui |
|
10 |
Pluvieux |
Moyen |
Normale |
Faible |
Oui |
|
11 |
Ensoleillé |
Moyen |
Normale |
Fort |
Oui |
|
12 |
Nuageux |
Moyen |
Élevée |
Fort |
Oui |
|
13 |
Nuageux |
Chaud |
Normale |
Faible |
Oui |
|
14 |
Pluvieux |
Moyen |
Élevée |
Fort |
Non |
Prévisions, Température, Humidité et Vent sont les quatre attributs qui déterminent chacun des exemples qui vont être fournis. On peut voir qu’il existe uniquement 36 exemples différents pour cette configuration d’attributs :
1.2. Arbre complet et optimisé généré par l’algorithme
Voici ce à quoi on devrait arriver à la fin de ce chapitre : un arbre tout beau tout propre généré sur base du tableau que je viens de vous donner. Si vous testez chaque branche avec la méthodologie expliquée au-dessus (§1.2.), vous vous apercevrez que l’arbre classe tous les exemples sans faute.
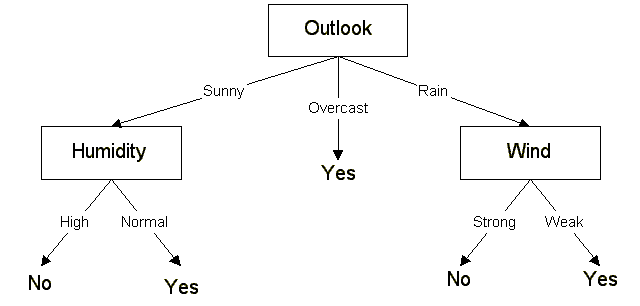
2. Explication de l’algorithme
L’algorithme ID3 se base sur le concept d’attributs et de classe de l’apprentissage automatique (sur classification discrète3). Cet algorithme recherche l’attribut le plus pertinent à tester pour que l’arbre soit le plus court et optimisé possible.
Pour trouver l’attribut à tester, Quinlan parle d’entropie. Pour définir l’entropie, il faut d’abord rappeler que la quantité minimale de données redondantes à ajouter pour qu’un message ayant une probabilité $p$ d’arriver sans être corrompu est $-\log_2(p)$. Une telle nécessité de stocker des données redondantes est assez évidente dans le cas de codes correcteurs d’erreurs par exemple1. Ne vous laissez pas avoir par le - devant le $\log$ : le logarithme d’un nombre compris entre 0 et 1 est toujours négatif. Il faut donc prendre son opposé avec le -. Rappelons également que l’entropie est la longueur minimale nécessaire pour coder la classe d’un membre pris au hasard dans le set d’exemples $S$. C’est en réalité de l’entropie de Shannon qu’il est question. On l’appelle ainsi car c’est une notion trouvée par l’ingénieur américain Claude Shannon.2
Tel que $p_c$ est la proportion d’exemples de $S$ ayant pour classe résultante $c$. Dans l’exemple d’au-dessus, les seules classes possibles sont Oui et Non. donc l’entropie vaut
D’ailleurs voici à quoi ressemble la fonction d’entropie pour un ensemble à deux classes possibles (Fig. 4)
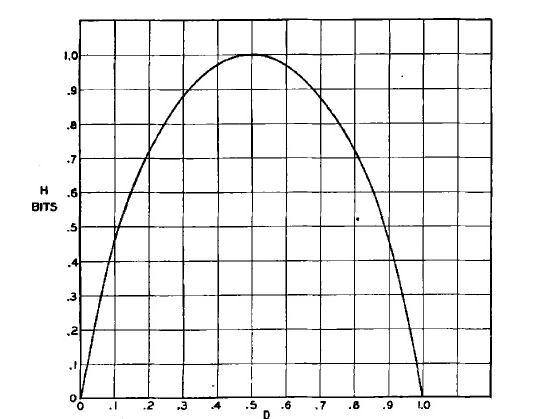
Remarquons quelque chose d’intéressant : cette fonction est parfaitement symétrique en prenant l’axe $x = \frac 12$. Et pour cause : la fonction d’entropie représente le "désordre" au sein du set (dans notre cas, ou du message dans le cas du code correcteur d’erreurs). Donc qu’il y ait 5 éléments d’une classe et 3 d’une autre ou inversement, le "désordre" reste le même car les proportions restent inchangées.
On peut également voir trois points intéressants sur ce graphique (il y a en réalité une infinité de points intéressants pour ceux comme moi à qui ce graphe parle mais bon mon but est de ne pas vous effrayer donc nous allons nous intéresser qu’à ces trois là maintenant  ). Ces trois points sont les points d’abscisse 0, 0.5 et 1. Vous voyez où je veux en venir ? Si l’entropie représente le désordre du set, c’est logique que le set ait l’entropie la plus élevée quand il est le plus désordonné. Et quand est-ce qu’il est le plus désordonné ? Quand il a autant d’objets de la première classe que d’objets de la deuxième classe. Logique non ? Et inversement : quand le set a une entropie nulle (qui vaut 0), c’est parce que c’est à ce moment que le désordre est le moins élevé. Et quand est-ce que le désordre est le moins élevé ? Quand tous les objets sont de la même classe. Donc quand la probabilité est soit minimum (0) soit maximum (1).
). Ces trois points sont les points d’abscisse 0, 0.5 et 1. Vous voyez où je veux en venir ? Si l’entropie représente le désordre du set, c’est logique que le set ait l’entropie la plus élevée quand il est le plus désordonné. Et quand est-ce qu’il est le plus désordonné ? Quand il a autant d’objets de la première classe que d’objets de la deuxième classe. Logique non ? Et inversement : quand le set a une entropie nulle (qui vaut 0), c’est parce que c’est à ce moment que le désordre est le moins élevé. Et quand est-ce que le désordre est le moins élevé ? Quand tous les objets sont de la même classe. Donc quand la probabilité est soit minimum (0) soit maximum (1).
Initialement, l’algorithme prend tout le set $S = \left\{J_1, J_2, J_3, ..., J_{14}\right\}$. Et comme 9 des 14 exemples donnent la réponse (ou classe) Oui et 5 sur 14 donnent la réponse (ou classe) Non,
On peut donc calculer4 que
Il faut savoir que, comme on peut le voir sur la Fig. 4,
Ce qui veut dire que pour tout ensemble $S$, le désordre de $S$ est toujours compris entre 0 et 1.
Maintenant que nous savons que l’entropie initiale du set est de 0.94, il nous faut savoir quel attribut tester en premier, puis en second, …, puis en n-ième.
Pour savoir quel attribut tester, il faut connaître la notion de gain d’entropie. Le gain est défini par un set d’exemples et par un attribut. Cette formule va donc servir à calculer ce que cet attribut apporte au désordre du set. Plus un attribut contribue au désordre, plus il est important de le tester pour séparer le set en plus petits sets ayant une entropie moins élevée.
L’attribut qui va être testé à ce nœud de l’arbre est le nœud qui va le plus réduire l’entropie. C’est logique : quand l’entropie vaut zéro, c’est qu’il n’y a qu’une seule classe représentée :
Ici, j’ai mis un n en évidence pour dire qu’il peut y avoir autant de classes que l’on veut. Mais si la probabilité d’une classe est 1, on a beau avoir 150 classes, leur probabilité sera nulle à chaque fois. On peut donc mettre le nombre de classes en évidence. Mais attention, si je mets n en évidence, c’est parce qu’il y a n classes de probabilité nulle, mais il y a aussi une classe de probabilité 1. Il y a donc n+1 classes différentes.
Toujours dans notre exemple du point 2, en considérant $S$ comme le set initial, pour déterminer l’attribut à tester, il faut calculer le gain de tous les attributs :
2.1. Calcul de gain d’entropie
2.1.1. Prévisions
L’attribut Prévisions a trois valeurs possibles : $\left\{\text{Ensoleillé}, \text{Nuageux}, \text{Pluvieux}\right\}$.
2.1.2. Vent
L’attribut Vent a quant à lui deux valeurs possibles : $\left\{\text{Faible}, \text{Fort}\right\}$.
2.1.3. Humidité
Humidité a également deux valeurs possibles : $\{\text{Élevée}, \text{Normale}\}$.
2.1.4. Température
Température a trois valeurs différentes possibles : $\{\text{Chaud}, \text{Chaud}, \text{Frais}\}$.
Récapitulons : $\text{Gain}(S, \text{Température}) < \text{Gain}(S, \text{Vent}) < \text{Gain}(S, \text{Humidité}) < \text{Gain}(S, \text{Prévisions})$. On peut voir que le plus grand gain est pour Prévisions. C’est donc Prévisions qui est le premier attribut testé dans l’arbre. Si on regarde chaque nœud fils, on remarque que pour le nœud Nuageux, tous les résultats sont positifs. Il n’y a donc pas d’attribut à tester ici, on peut directement étiqueter Oui. Voici à quoi ressemble notre arbre.

Image perdue
J’ai utilisé une notation entre crochets de la forme [n+, m-]. Cette notation veut dire que dans l’ensemble ayant n+m éléments, n sont positifs et m sont négatifs. Dans notre cas, les positifs sont les exemples étiquetés Oui et les négatifs sont ceux étiquetés Non bien entendu.
Il faut maintenant continuer à mettre des nœuds après Ensoleillé et Pluvieux car tous les exemples ne donnent pas le même résultat. Déterminons donc pour Ensoleillé quel est le meilleur attribut à tester en utilisant à nouveau le gain. Cependant il n’est plus utile de tester le gain de Prévisions étant donné qu’il vient d’être utilisé. Je vous donne juste les résultats, je vous laisse faire les calculs vous-même pour vous entrainer.
Rappel : pour ceux n’ayant pas de fonctionnalité $\log_2$ sur leur calculatrice :
Voici donc ce que vous devez normalement obtenir :
Donc récapitulons à nouveau :
Le plus grand gain est pour Humidité. D’ailleurs on peut voir que le gain est égal à l’entropie de $S_{\text{Ensoleillé}}$. Ça veut dire que tous les fils de Humidité donneront une étiquette. Voilà notre arbre jusqu’à présent. Il nous reste à continuer l’arbre du côté de Pluvieux. Voici les gains pour les différents attributs (à nouveau, il n’est pas nécessaire de tester Prévisions qui vient de l’être mais il faut tester Humidité qui n’a pas été testé de ce côté-là de la branche) :
Récapitulons une fois de plus :
Le plus grand gain est à nouveau de 0.971 et est pour Vent. Il nous faut donc tester Vent et vu que le gain est égal à l’entropie de $S_{\text{Pluvieux}}$, chaque nœud fils de Vent sera une étiquette.
Voici donc notre arbre. Il n’y a plus rien à faire étant donné qu’il ne reste aucun nœud qui n’est pas étiqueté. Le travail est donc accompli et voilà l’arbre que nous avons généré.

Si vous comparez l’arbre que nous venons de générer avec l’arbre que je vous ai donné en début de tutoriel, vous pouvez constater que c’est exactement le même. L’arbre est optimisé car il donne une étiquette en maximum deux tests alors qu’il y a 4 attributs différents.
Vous ne voyez peut-être pas l’utilité de cet arbre parce qu’ici il y a maximum 36 combinaisons des attributs et 14 nous sont déjà données. Mais imaginez maintenant que vous voulez faire un arbre qui va déterminer un diagnostic pour des malades. Comme il existe des milliers de maladies et encore plus de symptômes, l’arbre sera plus difficile à faire à la main. Ceci dit, tant que tous les exemples possibles n’ont pas été donnés il est possible que l’arbre contienne des erreurs. Mais nous y reviendrons plus tard. 
3. Algorithme et pseudo-code de l’algorithme ID3
Voici l’algorithme de génération d’un arbre de décision selon ID3 sous forme de pseudo-code. Ce chapitre est pour les programmeurs. Si vous êtes uniquement venus pour les maths, ce chapitre ne vous concerne pas directement et vous n’êtes pas obligés de lire ce qui suit.
Je ne vais pas détailler le pseudo-code, ça devrait sembler relativement clair. Et si vous avez tout de même besoin d’aide à la compréhension, regardez dans les commentaires, peut-être trouverez-vous votre réponse. Et si vous ne l’y trouvez pas, posez votre question sur les forums, c’est à ça qu’ils servent.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | FONCTION ID3
Entrée :
- exemples = liste d'exemples étiquetés
- questions = liste des attributs non utilisés jusqu'à présent
Retour :
- un nœud
DEBUT
SI exemples est vide, alors
Finir la fonction sans construire de nœud
FIN SI
SI tous les exemples sont la même classe, alors
Retourner une feuille ayant cette classe
FIN SI
SI questions est vide, alors
Retourner une feuille avec la classe la plus fréquente
FIN SI
q = attribut optimal (avec le plus grand gain d'entropie)
n = nouveau nœud créé qui testera l'attribut q
POUR CHAQUE v = valeur possible de q, FAIRE
e = l'ensemble des éléments de exemples ayant v comme valeur à l'attribut q
chaque nœud fils de n est créé par ID3(e, questions\{q})
FIN POUR CHAQUE
Retourner n
FIN
|
Notez que si la condition SI questions est vide est remplie, ça veut dire que deux exemples identiques mais étiquetés différemment ont été mis dans le set d’exemples de test.
4. Améliorations
Ici sont présentées d’abord les améliorations que l’on peut apporter aux notions vues au (§2.).5
Commençons par la fonction d’Entropie. Une petite étude mathématique nous montre que la probabilité d’une classe dans un set n’est autre que la longueur du sous-set de cette classe divisée par la longueur du set initial. Donc
Alors cette petite démonstration peut vous paraître rude, mais elle est très bien car elle nous permet de faire beaucoup moins de calculs. C’est très pratique tant pour programmer (car le programme sera plus rapide) que pour faire les calculs de tête (vous risquez beaucoup moins de faire des erreurs). On a donc simplifié notre splendide fonction d’entropie et on a gardé un indice sommatoire tout de même. Ouf ! 
Quid de la fonction de $\text{Gain}(S, A)$ ?
Cette fonction varie entre 0 et $\text{Entropie}(S)$ vu que :
Quand la somme vaut 0, $\text{Gain}(S, A)$ vaut $\text{Entropie}(S)$ ce qui est son maximum. C’est donc cet attribut qui va être choisi. Alors que si la somme vaut $\text{Entropie}(S)$, gain vaut 0 et donc cet attribut n’est pas intéressant à tester à ce moment vu qu’il ne réduit pas l’entropie (qui est, rappelons-le, le désordre des classifications du set). La seule chose qui nous intéresse dans cette fonction est donc la somme qui doit être la plus petite possible (il nous faut avoir le moins de désordre). On peut donc changer la fonction comme ceci :
Sauf que je viens de vous montrer comment améliorer la fonction d’entropie. On peut donc encore simplifier la fonction de gain !
Je ne pense pas que cette amélioration-ci ait réellement une influence en termes de performances lors d’un programme mais c’est plus facile de faire les calculs à la main avec cette formule. La double somme peut faire un petit peu peur, mais ce n’est pas bien compliqué : ça veut dire qu’on fait la somme sur tous les v, et que pour chaque v, on ajoute la somme sur tous les c.
PS : faites bien attention, ici c’est bien un indice sommatoire sur c dans les classes de $S_v$ et plus juste dans $S$. La raison est bien simple, c’est ce qui est expliqué juste au-dessus, c’est lié à la double somme.
Ces améliorations ne changent rien à l’algorithme. Ce sont juste de légères optimisations pour éviter de trop calculer. C’est pour ceux qui programment leur algorithme mais également pour ceux qui font leurs calculs sur papier et à la calculette (ou pour les plus balèzes, qui font les calculs de logarithmes avec leurs tables) et qui ne veulent pas tout le temps calculer les mêmes choses ce qui augmente la probabilité d’erreurs.
-
Pour plus d’informations, c’est ici et plus largement ici ou encore par ici. ↩
-
ici, la classification discrète s’oppose à la classification continue. Les mathématiques discrètes concernent les opérations sur des ensembles finis (ex : les possibilités d’un jet de dé : $\left\{1, 2, 3, 4, 5, 6\right\}$) alors que les mathématiques continues concernent les opérations sur des ensembles infinis (ex : $\mathbb R$) ↩
-
j’ai tendance à arrondir à la seconde décimale histoire que tout le monde ait une idée de l’ordre de grandeur pour pouvoir faire des comparaisons. Mais pour une question de lisibilité, je préfère mettre le symbole $=$ que le symbole $\simeq$. La valeur ici n’est donc pas précisément $0.94$ mais s’en rapproche assez fort. On peut donc se permettre une approximation. ↩
-
ce chapitre n’est pas indispensable à la lecture. C’est un développement mathématique sur les logarithmes qui permet de simplifier l’écriture et/ou le sens des formules. Vous pouvez soit l’ignorer et passer à la suite, soit regarder à quelles formules on arrive sans regarder le reste, soit suivre toute la pseudo-démonstration (qui s’apparente plus à un développement et à des substitutions). Je vous conseille de faire ce que votre cerveau pourra tolérer en terme de maths, je ne vous en voudrai pas si vous ne le lisez même pas ;) ↩
Une implémentation
5. Implémentation
Je vais vous proposer une implémentation détaillée en python3. Je vas vous guider étape par étape dans la réalisation de ce programme. Et pour ceux qui ne savent pas vraiment programmer ce n’est pas grave, le code complet sera mis à la fin.
Le code que je vous propose est une implémentation que j’ai choisie et que j’ai développée. Elle n’est pas la plus performante mais les choix sont avant tout pédagogiques.
Le code qui suit est pseudo-orienté objet (dans la mesures de ce que Python permet), il vous faut être relativement à l’aise avec cette notion pour pouvoir le comprendre !
5.1. Les types de données nécessaires
Commençons par déterminer de quelles structures de données nous allons avoir besoin. Voici ce que je propose, je vous laisse le lire, puis j’expliquerai.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | classe Nœud:
* enfants: dict
* attribut_testé: str
classe Feuille:
* étiquette: str
classe Exemple:
* étiquette: str
* attributs: dict
classe Ensemble:
* noms_attributs: list de str
* liste_exemples: list de Exemple
classe Arbre_ID3:
* arbre: Nœud/Feuille
* ensemble: Ensemble
|
Voilà le moment où je dois vous l’expliquer. J’ai donc fait un découpage en classes. Peut-être auriez-vous fait autrement mais voilà, c’est ce que j’ai choisi.
Pourquoi ces classes là ?
Bon pour commencer, laissez-moi expliquer la classe Arbre_ID3. Cette classe contient deux informations importantes :
- l’arbre en lui-même ;
- et l’ensemble de données sur lequel il est construit.
Cet ensemble, il est de classe Ensemble (oui je sais c’est pas très imaginatif mais au moins, c’est clair  ). La classe Ensemble quant à elle contient également deux informations mais ce ne sont pas du tout les mêmes :
). La classe Ensemble quant à elle contient également deux informations mais ce ne sont pas du tout les mêmes :
- le nom des attributs qui sont à utiliser ;
- et les exemples.
Le nom des attributs est stocké dans une liste (qui est un type interne à Python1) et les exemples sont également stockés dans une liste. Mais que contiennent ces listes me direz-vous !
… Mais que contiennent ces listes ?
Merci de poser la question, ça me permet de vous expliquer la classe Exemple !
La première liste, le nom des attributs ne contient que des chaines de caractères, ou des Strings. Ce type s’appelle str en Python. Par contre, la seconde liste, celle qui contient les exemples contient des… Exemples ! donc des objets de la classe Exemple.
Cette classe Exemple contient deux informations importantes :
- l’étiquette de l’exemple ;
- et ses attributs.
L’étiquette est une str alors que les attributs sont un dictionnaire ayant pour clef le nom de l’attribut et comme valeur la valeur de l’attribut. Logique, non ?
Je crois qu’on en a fini pour vous expliquer ce qui était contenu dans la variable ensemble de la classe Arbre_ID3… Mais il nous reste la variable arbre !
Cette variable arbre est soit un objet de type Feuille soit un objet de type Nœud. Étant donné que la notion d’arbre est un prérequis pour ce cours, je considère que vous connaissez ces deux termes et je ne m’attarderai pas dessus.
La classe Feuille ne contient qu’un élément de type str. C’est vrai que ce n’était pas obligatoire d’en faire une classe, mais je préférais pour une raison de clarté.
La classe Nœud quant à elle contient la valeur de l’attribut testé dans un str et un dictionnaire de Nœuds. Effectivement, c’est bien le principe : pour faire un arbre n-aire, il nous faut pouvoir mettre autant de fils que possible à chaque nœud.
Nous avons maintenant fait le tour des variables, nous pouvons passer à la phase de développement du code, du vrai ! 
5.2. Le code le vrai
La première chose que doit faire notre code, c’est savoir sur quelles données il va travailler. On pourrait soit rentrer toutes nos données de la classe Ensemble à la main, mais j’ai le sentiment que ça va être long, fastidieux et inutile… Je vous propose donc de créer une fonction qui va récupérer des données dans un fichier !
5.2.1. implémentation des types de données basiques
Cette fonction est une méthode de la classe Ensemble. Pourquoi ? C’est simple : on veut faire une fonction qui va remplir notre classe Ensemble et donc créer et modifier ses éléments. Cette méthode est donc dans notre classe Ensemble. Je propose même que ça fasse partie de notre constructeur ! je vais tout de même laisser la possibilité de créer un Ensemble simple, vous comprendrez plus tard pourquoi.
Voici donc le début de notre classe Ensemble qui contient un constructeur et une fonction qui nous permet d’alléger le code du constructeur.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 | class Ensemble: """ Un ensemble contient deux valeurs : - les noms des attributs (list) - les exemples (list) """ def __init__(self, chemin=""): """ chemin est l'emplacement du fichier contenant les données. Cette variable peut être non précisée en quel cas les variables seront initialisées comme des listes vides. """ #Python est un langage à typage dynamique fort, #il faut donc vérifier que l'utilisateur ne fait pas n'importe quoi #en passant autre chose qu'un str if not isinstance(chemin, str): raise TypeError("chemin doit être un str et non {}" \ .format(type(chemin))) if chemin == "": #initialisation en listes vides self.liste_attributs = list() self.liste_exemples = list() else: with open(chemin, 'r') as fichier: #on stocke chaque mot de la première ligne dans liste_attributs self.liste_attributs = \ fichier.readline().lower().strip().split(' ') #ensuite on stocke la liste d'exemples dans liste_exemples self.liste_exemples = self.liste_en_exemples( fichier.read().strip().lower().split('\n'), self.liste_attributs ) @staticmethod #fonction statique car ne dépend pas de l'objet mais est commune à toute instance de la classe def liste_en_exemples(exemples, noms_attributs): """ retourne une liste d'exemples sur base d'une liste de str contenant les valeurs et d'une liste de str contenant les noms des attributs """ #on initialise la liste à retourner ret = list() for ligne in exemples: #on stocke chaque mot de la ligne dans une liste attributs attributs = ligne.lower().strip().split(' ') #met l'étiquette par défaut si elle n'est pas dans la ligne etiquette = attributs[-1] if len(attributs) != len(noms_attributs) \ else "" #on ajoute un objet de type Exemple contenant la ligne ret.append(Exemple(noms_attributs, attributs[:len(noms_attributs)], etiquette)) return ret |
Voici comment nous allons coder le constructeur d’Exemple : cette fonction doit prendre en paramètres la liste contenant le nom des attributs, puis la liste contenant la valeur de chaque attribut, puis l’étiquette.
Voilà donc le début de notre classe Exemple :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 | class Exemple: """ Un exemple contient 2 valeurs : - un dictionnaire d'attributs (dict) - une étiquette (str) """ def __init__(self, noms_attributs, valeurs_attributs, etiquette=""): """ etiquette peut être non précisée en quel cas on aurait un exemple non étiqueté """ #si on a un problème de types if not isinstance(noms_attributs, list) \ or not isinstance(valeurs_attributs, list): raise TypeError("noms_attributs et valeurs_attributs doivent être" \ " des listes et pas des {0} et {1}" \ .format(type(noms_attributs), type(valeurs_attributs))) if not isinstance(etiquette, str): raise TypeError("etiquette doit être un str et pas un {}" \ .format(type(etiquette))) #si les deux listes n'ont pas le même nombre d'éléments if len(valeurs_attributs) != len(noms_attributs): raise ValueError("noms_attributs et valeurs_attributs doivent " \ "avoir le même nombre d'éléments") self.etiquette = etiquette self.dict_attributs = dict() #on ajoute chaque attribut au dictionnaire for i in range(len(noms_attributs)): self.dict_attributs[noms_attributs[i]] = valeurs_attributs[i] |
Lançons-nous maintenant dans la création de l’arbre en lui-même. Il nous faut donc manipuler la classe Arbre_ID3, et donc, la créer ! Le constructeur doit prendre une variable, à savoir le chemin vers le fichier de données à envoyer au constructeur de sa variable ensemble :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | class Arbre_ID3: """ Un arbre ID3 contient deux valeurs : - un ensemble d'exemples (Ensemble) - un arbre (Noeud) """ def __init__(self, chemin=""): """ chemin est l'emplacement du fichier contenant les données """ #initialisation de l'ensemble avec le fichier dans chemin self.ensemble = Ensemble(chemin) #initialisation du noeud principal de l'arbre self.arbre = None |
Voilà la base de notre classe. Sauf que jusqu’ici, on ne sait qu’initialiser les données, nous ce qu’on veut faire, c’est bien plus !
Il nous faut donc pouvoir créer l’arbre. Voici la méthode de Arbre_ID3 que je vous propose :
1 2 3 4 5 | def construire(self): """ génère l'arbre sur base de l'ensemble pré-chargé """ self.arbre = self.__construire_arbre(self.ensemble) |
Alors, vous aimez ? 
Bon d’accord, je le reconnais, je n’ai pas codé la réalisation de l’arbre… Mais c’est fait exprès ! J’ai créé une petite fonction toute simple à appeler par l’utilisateur pour que l’arbre se crée. Cette fonction appelle la fonction privée __construire_arbre.
5.2.2. La construction de l’arbre
Nous allons maintenant coder cette fonction, mais étape par étape.
5.2.2.1. Les tests
1 2 3 4 5 6 7 | def __construire_arbre(self, ensemble): """ fonction privée et récursive pour la génération de l'arbre """ if not isinstance(ensemble, Ensemble): raise TypeError("ensemble doit être un Ensemble et non un {}" \ .format(type(ensemble))) |
Voici la base de la définition de notre fonction (qui est donc toujours dans la classe Arbre_ID3). Si vous reprenez le pseudo-code que je vous ai donné deux chapitres au-dessus, vous pouvez voir qu’il nous faut tester si la liste d’exemples est vide, et si elle l’est, retourner une erreur. Nous allons utiliser les exceptions qui sont faites pour cela en python. Voici donc le test :
1 2 3 | #si la liste est vide if len(ensemble) == 0: raise ValueError("la liste d'exemples ne peut être vide !") |
Ici, je fais appel à la fonction len sur une classe qui n’est pas prévue à la base. Il nous faut donc ajouter la fonction __len__ à notre classe Ensemble. Étant donné qu’un minimum de connaissances en Python3 orienté objet est nécessaire, ce ne sera pas approfondi.
Voici donc la fameuse méthode qui nous permet de calculer la longueur de l’ensemble :
1 2 3 4 5 | def __len__(self): """ retourne la longueur de l'ensemble """ return len(self.liste_exemples) |
Je confirme, rien de bien compliqué, cependant, je n’ai jamais dit le contraire ! On aurait très bien pu faire sans, mais c’est quand même plus lisible comme ça. 
Après cela, il faut ajouter le test des classes. Comment on peut savoir si tous les exemples ont la même étiquette ? Facile, il suffit de les tester un par un et de voir si elle est différente du précédent (ou du premier)… Oui mais pour montrer qu’on a bien compris l’affaire, on peut tester l’entropie ! Que vaut l’entropie quand tous les exemples ont la même étiquette ? Elle vaut 0 !
1 2 3 4 | #testons si tous les exemples ont la même étiquette if ensemble.entropie() == 0: #on retourne l'étiquette en question return Feuille(ensemble.liste_exemples[0].etiquette) |
Ouille ! J’ai introduit ici beaucoup de choses ! Premièrement, j’ai créé une méthode entropie dans la classe Ensemble. Deuxièmement, j’ai créé la classe Feuille et son constructeur. Et le constructeur prend un seul paramètre (en plus de self bien entendu) de type str. Ce paramètre est l’étiquette vu que c’est la seule valeur que contient la classe Feuille.
Commençons par la classe Feuille, c’est le plus simple. Il suffit de créer une nouvelle classe et son constructeur, voici le code :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | class Feuille: """ Une feuille contient uniquement une valeur: - l'étiquette (str) """ def __init__(self, etiquette): """ etiquette doit obligatoirement être un str """ if not isinstance(etiquette, str): raise TypeError("etiquette doit être un str et pas un {}" \ .format(type(etiquette))) self.etiquette = etiquette |
Ce n’est pas bien compliqué. Par contre, pour la méthode d’entropie, ça risque de l’être un peu plus.
5.2.2.2. Le calcul d’entropie
Pour plus de clarté dans le code, je n’implémenterai pas l’amélioration proposée au chapitre précédent. Cependant, libre à vous de le faire si vous voulez !
Pour coder notre fonction, nous allons avoir besoin du logarithme inclus dans le module math. Donc :
1 | from math import log |
Ensuite nous allons créer la méthode dans notre classe Ensemble. Voici la méthode que je vous propose :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | def entropie(self): """ retourne l'entropie de Shannon de l'ensemble """ #initialisation de la variable retournée ret = 0 #pour chaque étiquette de l'ensemble for etiquette in self.etiquettes_possibles(): #on crée un sous-ensemble qui ne contient que les éléments de #self ayant etiquette comme étiquette sous_ensemble = self.sous_ensemble_etiquette(etiquette) #on ajoute |c| * log_2(|c|) à ret longueur_sous_ensemble = len(sous_ensemble) ret += longueur_sous_ensemble * log(longueur_sous_ensemble, 2) #on retourne log_2(|S|) - ret/|S| return log(len(self), 2) - ret/len(self) |
A nouveau, ce code introduit de nouvelles fonctions de la classe Ensemble : etiquettes_possibles() et sous_ensemble_etiquette().
Voici la fonction etiquettes_possibles. Elle a pour but de renvoyer une liste contenant toutes les étiquettes possibes dans l’ensemble d’exemples. :
1 2 3 4 5 6 7 8 9 10 11 12 13 | def etiquettes_possibles(self): """ retourne une liste contenant les étiquettes de l'ensemble """ #on initialise la valeur de retour ret = list() #pour chaque exemple de l'ensemble for exemple in self.liste_exemples: #si l'étiquette n'est pas déjà dans la liste if not exemple.etiquette in ret: #on l'ajoute ret.append(exemple.etiquette) return ret |
Et voici la fonction sous_ensemble_etiquette(). Son but à elle est de créer un sous-ensemble (comme son nom l’indique) ne reprenant que les exemples ayant la bonne étiquette :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | def sous_ensemble_etiquette(self, etiquette): """ retourne un ensemble contenant uniquement les exemples ayant etiquette comme étiquette """ #initialisation de la valeur de retour ret = Ensemble() #on copie la liste d'attributs ret.liste_attributs = self.liste_attributs[:] #pour chaque exemple de l'ensemble initial for exemple in self.liste_exemples: #si l'étiquette est bonne if exemple.etiquette == etiquette: #on l'ajoute au sous-ensemble ret.liste_exemples.append(exemple) return ret |
On peut donc reprendre le code de notre fonction de construction !
5.2.2.3. La liste d’attributs
Il nous faut maintenant tester si la liste d’attributs à tester est vide. Si elle l’est, il faut retourner une feuille avec l’étiquette la plus fréquente. Ce qui se fait de la manière suivante :
1 2 3 4 5 6 7 8 9 10 11 | #s'il ne reste d'attribut à tester if len(ensemble.liste_attributs) == 0: max, etiquette_finale = 0, "" #on teste toutes les étiquettes possibles de l'ensemble for etiquette in ensemble.etiquettes_possibles(): sous_ensemble = ensemble.sous_ensemble_etiquette(etiquette) #si c'est la plus fréquente, c'est celle qu'on choisit if len(sous_ensemble) > max: max, etiquette_finale = len(sous_ensemble), etiquette #et on la retourne dans une feuille return Feuille(etiquette_finale) |
5.2.2.4. Les nœuds enfants
Maintenant, il faut coder la partie la plus importante : la partie récursive !
C’est maintenant que l’on va pouvoir utiliser la puissance de la récursivité pour pouvoir générer tout l’arbre.
Commençons par trouver l’attribut optimal avec ceci :
1 | a_tester = self.attribut_optimal() |
La méthode attribut_optimal de la classe Ensemble peut être définie comme ceci :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | def attribut_optimal(self, ID3=True): """ retourne un str avec le nom de l'attribut à tester """ max, ret = float("-inf"), "" #pour chaque attribut for attribut in self.liste_attributs: gain = self.gain_entropie(attribut) #si le gain d'entropie est la plus grande if gain >= max: #on le garde en mémoire max, ret = gain, attribut #et on le retourne return ret |
Cette fonction nécessite que l’on code la fonction de gain d’entropie. Ici, deux choix s’offrent à nous :
- soit on prend la forme simple à implémenter mais non optimisée que voici :
1 2 3 4 5 6 7 8 9 10 11 12 13 | def gain_entropie(self, nom_attribut): """ retourne la perte d'entropie selon la définition de Ross Quinlan """ somme = 0 #pour chaque valeur de l'attribut en question for valeur in self.valeurs_possibles_attribut(nom_attribut): #déclaration de Sv sous_ensemble = self.sous_ensemble_attribut(nom_attribut, valeur) #somme = somme sur v de |Sv| * Entropie(Sv) somme += len(sous_ensemble) * sous_ensemble.entropie() #Gain(S, A) = Entropie(S) - 1/|S| * somme return self.entropie() - somme/len(self) |
- soit on prend la version optimisée donnée au chapitre précédent que je n’implémenterai pas comme mentionné plus haut.
Dans les deux cas, il est nécessaire de faire quelques fonctions en plus… Ces fonctions sont les suivantes : valeurs_possibles_attribut() et sous_ensemble_attribut().
La fonction valeurs_possibles_attribut() doit renvoyer une liste contenant toutes les valeurs que peut prendre l’attribut passé en paramètre. Voici son implémentation :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | def valeurs_possibles_attribut(self, nom_attribut): """ retourne une liste contenant toutes les valeurs possibles de l'attribut """ ret = list() #pour chaque exemple for exemple in self.liste_exemples: #si cette valeur n'est pas encore dans la liste if not exemple.dict_attributs[nom_attribut] in ret: #on l'ajoute ret.append(exemple.dict_attributs[nom_attribut]) #et on retourne la liste return ret |
Et sous_ensemble_attribut() doit renvoyer un sous-ensemble contenant uniquement une certaine valeur pour l’attribut. La voici :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | def sous_ensemble_attribut(self, nom_attribut, valeur): """ retourne un sous-ensemble contenant uniquement les exemples ayant la bonne valeur pour l'attribut """ ret = Ensemble() #on prend tous les attributs sauf celui passé en paramètre ret.liste_attributs = self.liste_attributs[:] ret.liste_attributs.remove(nom_attribut) #pour chaque exemple de l'ensemble for exemple in self.liste_exemples: #s'il a la bonne valeur if exemple.dict_attributs[nom_attribut] == valeur: #on l'ajoute ret.liste_exemples.append(exemple) #et on retourne la liste return ret |
Il nous reste une petite partie de la fonction de construction à faire, on doit faire la création du nœud à retourner. Et pour ce faire, il nous faut créer la classe Noeud ! La voici :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | class Noeud: """ Un noeud a deux valeurs : - un dictionnaire d'enfants (dict) - l'attribut testé (str) """ def __init__(self, attribut): """ attribut_teste est le nom de l'attribut stocké dans un str """ if not isinstance(attribut, str): raise TypeError("attribute_teste doit être un str et pas un {}" \ .format(type(attribut))) #initialisation des valeurs de l'objet self.enfants = dict() self.attribut_teste = attribut |
La suite et fin de notre fonction est donc la suivante :
1 2 3 4 5 6 7 8 9 10 | #si on arrive ici, on retourne d'office un nœud et pas une feuille noeud = Noeud(a_tester) #pour chaque valeur que peut prendre l'attribut à tester for valeur in ensemble.valeurs_possibles_attribut(a_tester): #on crée un sous-ensemble sous_ensemble = ensemble.sous_ensemble_attribut(a_tester, valeur) #et on en crée un nouveau nœud noeud.enfants[valeur] = self.__construire_arbre(sous_ensemble) #on retourne le nœud que l'on vient de créer return noeud |
Voici d’ailleurs le code complet de la fonction :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 | def __construire_arbre(self, ensemble): """ fonction privée et récursive pour la génération de l'arbre """ if not isinstance(ensemble, Ensemble): raise TypeError("ensemble doit être un Ensemble et non un {}" \ .format(type(ensemble))) #si la liste est vide if len(ensemble) == 0: raise ValueError("la liste d'exemples ne peut être vide !") #testons si tous les exemples ont la même étiquette if ensemble.entropie() == 0: #on retourne l'étiquette en question return Feuille(ensemble.liste_exemples[0].etiquette) #s'il ne reste d'attribut à tester if len(ensemble.liste_attributs) == 0: max, etiquette_finale = 0, "" #on teste toutes les étiquettes possibles de l'ensemble for etiquette in ensemble.etiquettes_possibles(): sous_ensemble = ensemble.sous_ensemble_etiquette(etiquette) #si c'est la plus fréquente, c'est celle qu'on choisit if len(sous_ensemble) > max: max, etiquette_finale = len(sous_ensemble), etiquette #et on la retourne dans une feuille return Feuille(etiquette_finale) a_tester = ensemble.attribut_optimal() #si on arrive ici, on retourne d'office un nœud et pas une feuille noeud = Noeud(a_tester) #pour chaque valeur que peut prendre l'attribut à tester for valeur in ensemble.valeurs_possibles_attribut(a_tester): #on crée un sous-ensemble sous_ensemble = ensemble.sous_ensemble_attribut(a_tester, valeur) #et on en crée un nouveau nœud noeud.enfants[valeur] = self.__construire_arbre(sous_ensemble) #on retourne le nœud que l'on vient de créer return noeud |
Maintenant, nous avons pu créer un arbre… Mais comment on sait si tout a bien fonctionné ?
C’est une excellente question ! C’est simple, on va l’afficher 
On peut donc :
- soit surcharger la fonction
__str__pour pouvoir l’utiliser dans un print ; - soit créer une nouvelle fonction pour pouvoir faire un affichage standard.
C’est personnellement la deuxième solution que je préfère car notre affichage est un peu spécial et tient sur plusieurs lignes. Je ne vois donc pas réellement comment dans quelle circonstance notre classe serait affichée dans un print si ce n’est quand elle est toute seule. Et c’est donc celle que je vais implémenter. Ceci-dit, libre à vous de faire l’autre, voire de faire les deux !
5.3. L’affichage de l’arbre
Je vous propose donc de faire une méthode de la sorte :
1 2 3 4 5 | def afficher(self): """ affiche l'entièreté de l'arbre à l'écran """ self.__afficher_arbre(self.arbre) |
Effectivement, je propose que l’on fasse comme pour la construction, une fonction privée. D’ailleurs, la voici. Comme vous pouvez le voir, j’ai utilisé une certaine convention de notation qui ne tient qu’à moi mais je la trouvais claire et jolie donc je l’ai gardée ! 
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | def __afficher_arbre(self, noeud, nb_tabs=0): """ selon la convention : <texte> <-> nom de l'attribut -<texte> <-> valeur de l'attribut .<texte> <-> feuille """ #si on a affaire à un nœud if isinstance(noeud, Noeud): #on affiche le nom de l'attribut testé print('\t' * nb_tabs + noeud.attribut_teste) #on parcourt ses enfants for enfant in noeud.enfants: #on affiche la valeur de l'attribut print('\t' * nb_tabs + '-' + str(enfant)) self.__afficher_arbre(noeud.enfants[enfant], nb_tabs+1) #si c'est une feuille elif isinstance(noeud, Feuille): #on affiche l'étiquette print('\t' * nb_tabs + '.' + noeud.etiquette) else: raise TypeError("noeud doit être un Noeud/Feuille et pas un {}" \ .format(type(noeud))) |
Nous avons donc maintenant fini l’implémentation de l’algorithme ID3 !
Sauf que comme ça, il ne nous sert à rien ! L’intérêt de ces arbres de décisions, c’est de pouvoir étiqueter des exemples externes. Il nous faut donc une méthode pour étiqueter un nouvel exemple. Cette méthode fait donc bien entendu partie de la classe Arbre_ID3. Voici ce que je vous propose :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | def etiqueter(self, exemple): """ assigne la bonne étiquette à l'exemple passé en paramètre """ #on initialise le nœud actuel avec le haut de l'arbre noeud_actuel = self.arbre #tant que l'on est sur un nœud et pas sur une feuille, #on continue d'explorer while not isinstance(noeud_actuel, Feuille): #pour savoir quel est le prochain nœud, on récupère d'abord #l'attribut testé avec noeud_actuel.attribut_teste puis on récupère #la valeur de l'exemple pour cet attribut avec #exemple.dict_attributs[noeud_actuel.attribut_teste] #puis on prend l'enfant de noeud_actuel ayant cette valeur. valeur = exemple.dict_attributs[noeud_actuel.attribut_teste] noeud_actuel = noeud_actuel.enfants[valeur] #on finit en donnant comme étiquette l'étiquette #contenue dans la feuille finale exemple.etiquette = noeud_actuel.etiquette |
Je vous laisse améliorer le code si bon vous semble. Je vous le donne en entier au cas où certains auraient mal copié ou se seraient trompés ou n’auraient pas réussi à tout comprendre.
Afficher/Masquer le contenu masqué1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 | """ écrit par poupou9779 pour Zeste de Savoir """ from math import log class Feuille: """ Une feuille contient uniquement une valeur: - l'étiquette (str) """ def __init__(self, etiquette): """ etiquette doit obligatoirement être un str """ if not isinstance(etiquette, str): raise TypeError("etiquette doit être un str et pas un {}" \ .format(type(etiquette))) self.etiquette = etiquette class Noeud: """ Un noeud a deux valeurs : - un dictionnaire d'enfants (dict) - l'attribut testé (str) """ def __init__(self, attribut): """ attribut_teste est le nom de l'attribut stocké dans un str """ if not isinstance(attribut, str): raise TypeError("attribute_teste doit être un str et pas un {}" \ .format(type(attribut))) #initialisation des valeurs de l'objet self.enfants = dict() self.attribut_teste = attribut class Exemple: """ Un exemple contient 2 valeurs : - un dictionnaire d'attributs (dict) - une étiquette (str) """ def __init__(self, noms_attributs, valeurs_attributs, etiquette=""): """ etiquette peut être non précisée en quel cas on aurait un exemple non étiqueté """ #si on a un problème de types if not isinstance(noms_attributs, list) \ or not isinstance(valeurs_attributs, list): raise TypeError("noms_attributs et valeurs_attributs doivent être" \ " des listes et pas des {0} et {1}" \ .format(type(noms_attributs), type(valeurs_attributs))) if not isinstance(etiquette, str): raise TypeError("etiquette doit être un str et pas un {}" \ .format(type(etiquette))) #si les deux listes n'ont pas le même nombre d'éléments if len(valeurs_attributs) != len(noms_attributs): raise ValueError("noms_attributs et valeurs_attributs doivent " \ "avoir le même nombre d'éléments") self.etiquette = etiquette self.dict_attributs = dict() #on ajoute chaque attribut au dictionnaire for i in range(len(noms_attributs)): self.dict_attributs[noms_attributs[i]] = valeurs_attributs[i] class Ensemble: """ Un ensemble contient deux valeurs : - les noms des attributs (list) - les exemples (list) """ def __init__(self, chemin=""): """ chemin est l'emplacement du fichier contenant les données. Cette variable peut être non précisée en quel cas les variables seront initialisées comme des listes vides. """ #Python est un langage à typage dynamique fort, #il faut donc vérifier que l'utilisateur ne fait pas n'importe quoi #en passant autre chose qu'un str if not isinstance(chemin, str): raise TypeError("chemin doit être un str et non {}" \ .format(type(chemin))) if chemin == "": #initialisation en listes vides self.liste_attributs = list() self.liste_exemples = list() else: with open(chemin, 'r') as fichier: #on stocke chaque mot de la première ligne dans liste_attributs self.liste_attributs = \ fichier.readline().lower().strip().split(' ') #ensuite on stocke la liste d'exemples dans liste_exemples self.liste_exemples = self.liste_en_exemples( fichier.read().strip().lower().split('\n'), self.liste_attributs ) def __len__(self): """ retourne la longueur de l'ensemble """ return len(self.liste_exemples) @staticmethod def liste_en_exemples(exemples, noms_attributs): """ retourne une liste d'exemples sur base d'une liste de str contenant les valeurs et d'une liste de str contenant les noms des attributs """ #on initialise la liste à retourner ret = list() for ligne in exemples: #on stocke chaque mot de la ligne dans une liste attributs attributs = ligne.lower().strip().split(' ') #met l'étiquette par défaut si elle n'est pas dans la ligne etiquette = attributs[-1] if len(attributs) != len(noms_attributs) \ else "" #on ajoute un objet de type Exemple contenant la ligne ret.append(Exemple(noms_attributs, attributs[:len(noms_attributs)], etiquette)) return ret def etiquettes_possibles(self): """ retourne une liste contenant les étiquettes de l'ensemble """ #on initialise la valeur de retour ret = list() #pour chaque exemple de l'ensemble for exemple in self.liste_exemples: #si l'étiquette n'est pas déjà dans la liste if not exemple.etiquette in ret: #on l'ajoute ret.append(exemple.etiquette) return ret def sous_ensemble_etiquette(self, etiquette): """ retourne un ensemble contenant uniquement les exemples ayant etiquette comme étiquette """ #initialisation de la valeur de retour ret = Ensemble() #on copie la liste d'attributs ret.liste_attributs = self.liste_attributs[:] #pour chaque exemple de l'ensemble initial for exemple in self.liste_exemples: #si l'étiquette est bonne if exemple.etiquette == etiquette: #on l'ajoute au sous-ensemble ret.liste_exemples.append(exemple) return ret def sous_ensemble_attribut(self, nom_attribut, valeur): """ retourne un sous-ensemble contenant uniquement les exemples ayant la bonne valeur pour l'attribut """ ret = Ensemble() #on prend tous les attributs sauf celui passé en paramètre ret.liste_attributs = self.liste_attributs[:] ret.liste_attributs.remove(nom_attribut) #pour chaque exemple de l'ensemble for exemple in self.liste_exemples: #s'il a la bonne valeur if exemple.dict_attributs[nom_attribut] == valeur: #on l'ajoute ret.liste_exemples.append(exemple) #et on retourne la liste return ret def entropie(self): """ retourne l'entropie de Shannon de l'ensemble """ #initialisation de la variable retournée ret = 0 #pour chaque étiquette de l'ensemble for etiquette in self.etiquettes_possibles(): #on crée un sous-ensemble qui ne contient que les éléments de #self ayant etiquette comme étiquette sous_ensemble = self.sous_ensemble_etiquette(etiquette) #on ajoute |c| * log_2(|c|) à ret longueur_sous_ensemble = len(sous_ensemble) ret += longueur_sous_ensemble * log(longueur_sous_ensemble, 2) #on retourne log_2(|S|) - ret/|S| return log(len(self), 2) - ret/len(self) def attribut_optimal(self): """ retourne un str avec le nom de l'attribut à tester """ max, ret = float("-inf"), "" #pour chaque attribut for attribut in self.liste_attributs: gain = self.gain_entropie(attribut) #si le gain d'entropie est le plus grand if gain >= max: #on le garde en mémoire max, ret = gain, attribut #et on le retourne return ret def valeurs_possibles_attribut(self, nom_attribut): """ retourne une liste contenant toutes les valeurs possibles de l'attribut """ ret = list() #pour chaque exemple for exemple in self.liste_exemples: #si cette valeur n'est pas encore dans la liste if not exemple.dict_attributs[nom_attribut] in ret: #on l'ajoute ret.append(exemple.dict_attributs[nom_attribut]) #et on retourne la liste return ret def gain_entropie(self, nom_attribut): """ retourne la perte d'entropie selon la définition de Ross Quinlan """ somme = 0 #pour chaque valeur de l'attribut en question for valeur in self.valeurs_possibles_attribut(nom_attribut): #déclaration de Sv sous_ensemble = self.sous_ensemble_attribut(nom_attribut, valeur) #somme = somme sur v de |Sv| * Entropie(Sv) somme += len(sous_ensemble) * sous_ensemble.entropie() #Gain(S, A) = Entropie(S) - 1/|S| * somme return self.entropie() - somme/len(self) class Arbre_ID3: """ Un arbre ID3 contient deux valeurs : - un ensemble d'exemples (Ensemble) - un arbre (Noeud) """ def __init__(self, chemin=""): """ chemin est l'emplacement du fichier contenant les données """ #initialisation de l'ensemble avec le fichier dans chemin self.ensemble = Ensemble(chemin) #initialisation du noeud principal de l'arbre self.arbre = None def construire(self): """ génère l'arbre sur base de l'ensemble pré-chargé """ self.arbre = self.__construire_arbre(self.ensemble) def __construire_arbre(self, ensemble): """ fonction privée et récursive pour la génération de l'arbre """ if not isinstance(ensemble, Ensemble): raise TypeError("ensemble doit être un Ensemble et non un {}" \ .format(type(ensemble))) #si la liste est vide if len(ensemble) == 0: raise ValueError("la liste d'exemples ne peut être vide !") #testons si tous les exemples ont la même étiquette if ensemble.entropie() == 0: #on retourne l'étiquette en question return Feuille(ensemble.liste_exemples[0].etiquette) #s'il ne reste d'attribut à tester if len(ensemble.liste_attributs) == 0: max, etiquette_finale = 0, "" #on teste toutes les étiquettes possibles de l'ensemble for etiquette in ensemble.etiquettes_possibles(): sous_ensemble = ensemble.sous_ensemble_etiquette(etiquette) #si c'est la plus fréquente, c'est celle qu'on choisit if len(sous_ensemble) > max: max, etiquette_finale = len(sous_ensemble), etiquette #et on la retourne dans une feuille return Feuille(etiquette_finale) a_tester = ensemble.attribut_optimal() #si on arrive ici, on retourne d'office un nœud et pas une feuille noeud = Noeud(a_tester) #pour chaque valeur que peut prendre l'attribut à tester for valeur in ensemble.valeurs_possibles_attribut(a_tester): #on crée un sous-ensemble sous_ensemble = ensemble.sous_ensemble_attribut(a_tester, valeur) #et on en crée un nouveau nœud noeud.enfants[valeur] = self.__construire_arbre(sous_ensemble) #on retourne le nœud que l'on vient de créer return noeud def afficher(self): """ affiche l'entièreté de l'arbre à l'écran """ self.__afficher_arbre(self.arbre) def __afficher_arbre(self, noeud, nb_tabs=0): """ selon la convention : <texte> <-> nom de l'attribut -<texte> <-> valeur de l'attribut .<texte> <-> feuille """ #si on a affaire à un nœud if isinstance(noeud, Noeud): #on affiche le nom de l'attribut testé print('\t' * nb_tabs + noeud.attribut_teste) #on parcourt ses enfants for enfant in noeud.enfants: #on affiche la valeur de l'attribut print('\t' * nb_tabs + '-' + str(enfant)) self.__afficher_arbre(noeud.enfants[enfant], nb_tabs+1) #si c'est une feuille elif isinstance(noeud, Feuille): #on affiche l'étiquette print('\t' * nb_tabs + '.' + noeud.etiquette) else: raise TypeError("noeud doit être un Noeud/Feuille et pas un {}" \ .format(type(noeud))) def etiqueter(self, exemple): """ assigne la bonne étiquette à l'exemple passé en paramètre """ #on initialise le nœud actuel avec le haut de l'arbre noeud_actuel = self.arbre #tant que l'on est sur un nœud et pas sur une feuille, #on continue d'explorer while not isinstance(noeud_actuel, Feuille): #pour savoir quel est le prochain nœud, on récupère d'abord #l'attribut testé avec noeud_actuel.attribut_teste puis on récupère #la valeur de l'exemple pour cet attribut avec #exemple.dict_attributs[noeud_actuel.attribut_teste] #puis on prend l'enfant de noeud_actuel ayant cette valeur. valeur = exemple.dict_attributs[noeud_actuel.attribut_teste] noeud_actuel = noeud_actuel.enfants[valeur] #on finit en donnant comme étiquette l'étiquette #contenue dans la feuille finale exemple.etiquette = noeud_actuel.etiquette def exemple_utilisation(): #exemple d'utilisation arbre = Arbre_ID3('datas PlayTennis.txt') arbre.construire() arbre.afficher() # il faut mettre les mots dans la même langue que l'ensemble choisi exemple = Exemple(["outlook", "temperature", "humidity", "wind"], ["sunny", "29.5", "normal", "strong"]) print("etiquette : '{}'".format(exemple.etiquette)) arbre.etiqueter(exemple) print("etiquette : '{}'".format(exemple.etiquette)) if __name__ == "__main__": exemple_utilisation() |
Je vous donne également l’exemple utilisé dans ce cours pour que vous puissiez voir à quel point votre code est magnifique !
Le voici :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | Prévisions Température Humidité Vent Ensoleillé Chaud Élevée Faible Non Ensoleillé Chaud Élevée Fort Non Nuageux Chaud Élevée Faible Oui Pluvieux Moyen Élevée Faible Oui Pluvieux Frais Normale Faible Oui Pluvieux Frais Normale Fort Non Nuageux Frais Normale Fort Oui Ensoleillé Moyen Élevée Faible Non Ensoleillé Frais Normale Faible Oui Pluvieux Moyen Normale Faible Oui Ensoleillé Moyen Normale Fort Oui Nuageux Moyen Élevée Fort Oui Nuageux Chaud Normale Faible Oui Pluvieux Moyen Élevée Fort Non |
PS : il se peut qu’il y ait des problèmes d’affichage d’accents avec les différents terminaux et invites de commande. Donc soit vous vous débarassez froidement des accents, soit vous configurez votre terminal, soit vous utilisez l’exemple en anglais que voici :
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | Outlook Temperature Humidity Wind Sunny Hot High Weak No Sunny Hot High Strong No Overcast Hot High Weak Yes Rain Mild High Weak Yes Rain Cool Normal Weak Yes Rain Cool Normal Strong No Overcast Cool Normal Strong Yes Sunny Mild High Weak No Sunny Cool Normal Weak Yes Rain Mild Normal Weak Yes Sunny Mild Normal Strong Yes Overcast Mild High Strong Yes Overcast Hot Normal Weak Yes Rain Mild High Strong No |
-
on parle de built-in type ↩
Et voilà, nous en avons fini pour l’algorithme ID3 et son implémentation. On souffle un bon coup, et puis on se lance sur son successeur : C4.5 !