La médaille Fields, c'est la plus prestigieuse des récompenses en mathématiques, souvent appelée "prix Nobel des mathématiques". Quelques différences distinguent toutefois la médaille Fields : celle-ci n'est remise qu'une fois tous les quatre ans à au plus quatre mathématiciens de moins de 40 ans.
Cette année, le Congrès International des Mathématiciens se tient à Séoul du 13 au 21 août et c'est lors de la cérémonie d'ouverture qu'a été dévoilée la cuvée 2014 de la médaille. Les heureux lauréats sont (par ordre alphabétique comme le veut la tradition) le franco-brésilien Artur Avila, le canadien-américain Manjul Bhargava, l'autrichien Martin Hairer et l'iranienne Maryam Mirzakhani.
Deux faits marquants sont à retenir dans ce palmarès :
- Maryam Mirzakhani devient la première femme à obtenir la médaille Fields. Depuis plusieurs semaines déjà les rumeurs allaient bon train sur la présence d'une femme parmi les quatre lauréats. Une bonne nouvelle confirmée ce 13 août, cette récompense est doublement symbolique puisqu'il s'agit également de la première médaille pour l'Iran qui est l'un des plus grands pays dans l'histoire des mathématiques.
- Artur Avila devient le douzième français à obtenir cette médaille. Il succède à Cédric Villani et Ngô Bảo Châu qui avaient obtenus la médaille en 2010 et confirme ainsi le dynamisme de l'école mathématique française. Il faut remonter sept éditions en arrière, en 1990, pour trouver un palmarès sans français !
Artur Avila

À 35 ans, Artur Avila est le benjamin de cette promotion 2014. Touche-à-tout, il a déjà écrit avec une trentaine de collaborateurs différents plusieurs dizaines d'articles traitant de sujets divers. L'un de ses sujets de prédilection pour lequel il a obtenus des résultats importants salués par le jury de la médaille Fields concerne les systèmes dynamiques.
Regardons un exemple de système dynamique tel qu'Avila a étudié. Considérons une équation du type $a\times x\times (1-x)$ où $a$ est un nombre compris entre 0 et 4. Prenons par exemple $a=2$ on a donc l'équation $2x(1-x)$.
Prenons maintenant un nombre compris entre 0 et 1, par exemple 0,1 et mettons le dans l'équation. On trouve $2\times 0,1\times (1-0,1)= 0,18$. Prenons alors 0,18 et recommençons : $2\times 0,18\times (1-0,18)= 0,2952$. Et ainsi de suite, on reprend à chaque fois le nombre obtenu et on le remet dans l'équation. En répétant le processus on obtient la suite de nombres suivante :
0,1 - 0,18 - 0,2952 - 0,4161 - 0,4859 - 0,4996 - 0,4999 - …
On remarque que la suite se rapproche de plus en plus de 0,5 ! En revanche, si à la place de 2, on prend 3,6 pour $a$, on obtient la suite suivante :
0,1 - 0,324 - 0,7884 - 0,6004 - 0,8637 - 0,4238 - 0,8790 - …
Cette fois, les nombres ne tendent pas vers une limite, mais se baladent de manière apparemment aléatoire entre 0 et 1. On appelle ceci un comportement chaotique.
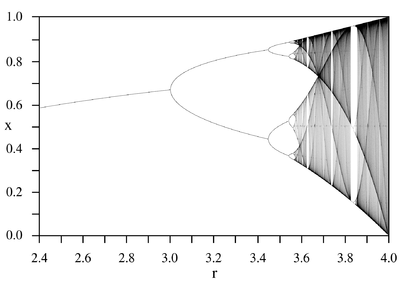
Si on trace sur un graphique les nombres dont la suite se rapproche en fonction de $a$, on obtient ceci :
Magnifique, n'est-ce pas ? En dessous de 3 il n'y a qu'un seul attracteur, puis il y en a 2, puis 4 et plus $a$ se rapproche de 4, plus le comportement semble chaotique. Comprendre ces phénomènes, et pouvoir prédire le comportement de la suite en fonction de $a$ fait partie des travaux qu'a mené Avila et qui lui ont valu cette médaille.
Manjul Bhargava

L' américain-canadien Manjul Bhargava est lui le doyen de cette promotion. Le théoricien des nombres vient de fêter ses 40 ans le 8 août. Juste à temps donc pour lui puisque 40 ans est l'âge limite auquel il est possible de recevoir la médaille (en réalité, il faut avoir moins de 40 ans au 1er janvier de l'année de remise de la médaille, Bhargava est donc bien dans les temps).
Lors de ses études, Manjul Bhargava a eu pour directeur de thèse l'un des plus célèbres mathématiciens de notre époque : Andrew Wiles, le tombeur du théorème de Fermat qui fut l'un des plus grands problèmes mathématiques jusqu'à sa résolution dans les années 1990. Au moment de sa résolution, en 1994, Wiles avait tout juste dépassé l'âge limite pour obtenir la médaille Fields. Pourtant la découverte était telle qu'il a été envisagé un temps de lui remettre quand-même la médaille. Mais une faille fut découverte dans la démonstration, Wiles finit par réussir à la combler, mais trop tard pour la médaille ! Aujourd'hui, cette injustice est quelque peu réparée puisque c'est un de ses étudiants qui est récompensé.
Le mathématicien Henri Poincaré avait affirmé que "les mathématiciens n'étudient pas des objets mais les relations entre ces objets". Par exemple, quand on étudie les nombres, ce qui est intéressant, c'est avant tout les liens qui existent entre eux et ces liens sont créés par des opérations telles que l'addition ou la multiplication.
Seulement, les mathématiciens n'étudient pas que les nombres, mais aussi des objets plus complexes comme par exemple ce qu'on appelle des polynômes. Le grand mathématicien Carl Friedrich Gauss avait déjà étudié des opérations entre des polynômes du type $ax^2+bxy+cy^2$. Manjul Bhargava a été récompensé entre autres pour avoir jeté de nouvelles lumières et poursuivi ces travaux du mathématicien allemand. Il a découvert et étudié de nouvelles opérations ayant des propriétés très intéressantes et créant de nouveaux liens entre les polynômes, bien au delà de ceux initialement étudiés par Gauss.
Martin Hairer

Martin Hairer est un probabiliste. La théorie des probabilités est un domaine encore relativement jeune des mathématiques ayant obtenu sa première médaille Fields en 2006 avec le français Wendelin Werner. Cette nouvelle médaille confirme qu'il s'agit d'une discipline en vogue et dynamique.
Plus précisément, Hairer a obtenu la médaille pour ses travaux sur les équations différentielles stochastiques (stochastique est un synonyme d'aléatoire, cela signifie que le hasard et donc la théorie des probabilités interviennent).
En sciences physiques, quand on veut prévoir l'évolution d'un système, on est souvent confronté à des équations différentielles. Par exemple si vous lancez une pomme devant vous, il est possible de calculer sa trajectoire : vous savez que la pomme est attirée par la Terre, donc son vecteur vitesse va varier en se dirigeant de plus en plus vers le bas, et une fois que vous avez le vecteur vitesse, vous pouvez reconstituer la trajectoire. En termes mathématiques ceci se traduit précisément par les équations différentielles.
Imaginez maintenant qu'il y ait du vent, mais un vent non régulier, qui change sans cesse de force et de direction. L'objet que vous lancez va donc subir des influences que vous ne pouvez pas maîtriser, des influences aléatoires. En introduisant cet aléa dans les équations, on obtient une équation différentielle stochastique. Au delà des lancers de pommes, ce genre d'équation se retrouve dans énormément de systèmes physiques. Malheureusement, ces équations sont en général extrêmement dures à traiter et à comprendre. Hairer a créé des techniques permettant de mieux cerner et analyser de nombreuses équations de ce type.
Maryam Mirzakhani

Des quatre lauréats de cette année, l'iranienne Maryam Mirzakhani était sans doute celle qui était la plus attendue et celle dont on va le plus parler dans le monde. Et pour cause : c'est la première femme à obtenir cette médaille ! Une étape importante vers plus de parité dans le monde de mathématiques qui reste majoritairement masculin. Espérons que cette médaille pourra inspirer d'autres jeunes filles à se lancer dans les maths.
En mathématiques, la dimension d'un ensemble d'objets, c'est le nombre de nombres qu'il faut pour le définir. Par exemple, vous savez certainement que nous vivons dans un monde en 3 dimensions, car pour repérer un point dans l'espace, il faut donner ses 3 coordonnées par exemple selon les trois directions avant/arrière, gauche/droite et haut/bas. Mais de la même manière, on peut aussi dire que quand on fait de la géométrie dans le plan, l'ensemble des triangles est de dimension 6. En effet, chacun des trois sommets est repéré par 2 coordonnées dans le plan, il faut donc bien 6 nombres au total pour déterminer entièrement un triangle.
De la même façon que l'on peut se déplacer d'un point à un autre dans notre espace à 3 dimensions et que l'on peut calculer la distance entre eux deux, il est également possible de passer d'un triangle à l'autre dans l'espace des triangles et de se demander quel est le plus court chemin de l'un à l'autre.
Les recherches de Maryam Mirzakhani se posent ce genre de questions, seulement ce n'est ni dans l'espace en 3 dimensions, ni dans celui des triangles, mais dans certains espaces formés de ce que l'on appelle des surfaces de Riemann. Les surfaces de Riemann sont des objets à la fois mystérieux et absolument fascinants en mathématiques. Ce sont des surfaces, comme le sont par exemple les sphères ou les tores (surfaces en forme de bouées), mais dans lesquels on a intégré des nombres.
Si vous tracez une droite, vous savez sans doute qu'il est possible d'y intégrer les nombres réels, par exemple de la façon suivante :
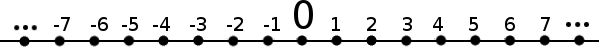
Pour les surfaces de Riemann, ça se passe un peu de la même manière, mais avec les nombres complexes à la place des nombres réels. Les nombres complexes sont une extension des nombres réels dans laquelle il est également possible de faire des racines carrées de nombres négatifs. Les surfaces de Riemann peuvent se classer en plusieurs catégories selon un nombre entier nommé leur genre et noté $g$, qui désigne le nombre "trous" qu'il y a dans la surface. La dimension des surfaces de Riemann de genre $g$ est $6g-6$.
Liens
Voici quelques références pour en savoir plus :
- La page wikipedia de la médaille Fields.
- L'annonce des lauréats sur le site de l'Union Mathématique Internationale.
- Le site du Congrès International des Mathématiciens de Séoul.