Du 1er au 9 août 2018, à Rio de Janeiro, s’est tenu le Congrès international des mathématiciens, au cours duquel, conformément à la tradition, la médaille Fields a été remise à de jeunes chercheurs en mathématiques.

Le Congrès est le grand rendez-vous des mathématiciens ! Tous les quatre ans, il permet aux invités de se rencontrer, d’échanger et d’assister à des conférences par d’éminents chercheurs. Le moment fort de cet événement est la cérémonie de remise de la médaille Fields, qui récompense au plus quatre mathématiciens ou mathématiciennes de moins de 40 ans. Son prestige est tel qu’on la compare souvent au prix Nobel !
Cette année, les quatre lauréats sont, dans l’ordre alphabétique :
- l’irano-britannique Caucher Birkar de l’Université de Cambridge,
- l’italien Alessio Figalli de l’École polytechnique fédérale de Zurich,
- l’allemand Peter Scholze de l’Université de Bonn,
- l’australien Akshay Venkatesh de l’Université de Stanford.
Présentons ces mathématiciens et leurs travaux plus en détails !
- Caucher Birkar, spécialiste de la géométrie algébrique
- Alessio Figalli, spécialiste du transport optimal
- Peter Scholze, spécialiste de la géométrie algébrique arithmétique
- Akshay Venkatesh, à la croisée des mondes
Caucher Birkar, spécialiste de la géométrie algébrique
Caucher Birkar est un mathématicien irano-britannique de 40 ans (en 2018) travaillant à l’Université de Cambridge. Il est né dans une ferme au Kurdistan, près de la frontière entre l’Iran et l’Irak. Dans son enfance, il a connu les huit ans de guerre entre les deux pays. Pendant ses études, il est parti d’Iran et a obtenu l’asile au Royaume-Uni en tant que réfugié. Et quelques heures après la remise de sa médaille, elle lui a été volée en même temps que son porte-feuille ! Heureusement, elle a pu être remplacée ; tout est bien qui finit bien.
Il travaille en particulier sur la géométrie birationnelle, qui est un sous domaine de la géométrie algébrique. Les travaux de Caucher Birkar dans cette discipline lui ont valu la médaille Fields « pour sa preuve du caractère borné des variétés de Fano et pour des contributions au programme du modèle minimal1 ».

Qu’est-ce que la géométrie algébrique ?
La géométrie algébrique est la discipline des mathématiques qui étudie les formes géométriques pouvant être décrites par des équations polynomiales. Une équation polynomiale est une équation obtenue en combinant les inconnues à l’aide d’additions, de soustractions et de multiplications par des constantes. Quand on interprète les inconnues comme des coordonnées de points, l’ensemble des solutions de l’équation correspond alors à une forme géométrique, qu’on appelle une variété algébrique.
Peut-être avez-vous déjà fait de la géométrie algébrique sans le savoir ? Pour le savoir, regardons de plus près deux exemples qui vous seront peut-être familiers.
Une droite du plan peut être représentée par son équation cartésienne. Autrement dit, pour une droite donnée, il est possible de trouver trois réels , et tels qu’un point appartienne à la droite si et seulement si ses coordonnées vérifient l’équation :
Les inconnues sont combinées au moyen d’additions et de soustractions, mais aussi de multiplications par des constantes : il s’agit donc d’une équation polynomiale. En conséquence, les droites du plan sont des variétés algébriques !
Les cercles sont également des variétés algébriques. En effet, un cercle de centre et de rayon a l’équation polynomiale suivante pour équation cartésienne :
Les exemples ci-dessus font intervenir des polynômes réels, mais la notion de variété algébrique se généralise aux polynômes sur d’autres corps, tels que les complexes ou tout autre corps aux propriétés adéquates.
Catégoriser les variétés algébriques
Les mathématiciens cherchent à catégoriser les variétés algébriques en familles dont les membres peuvent être métamorphosés les uns dans les autres à l’aide de transformations particulières, dites birationnelles. Le champ d’étude associé forme ce qu’on appelle la géométrie birationnelle.
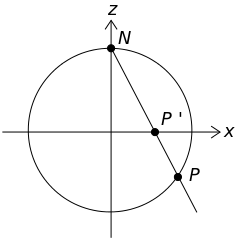
Par exemple, il est possible de transformer un cercle en une droite et réciproquement en utilisant une telle transformation. Cela créé, en un sens, une équivalence entre un cercle et une droite : les deux formes font partie d’une même famille.
Un des sujets phares de la géométrie birationnelle est le développement d’un programme du modèle minimal, autrement dit l’élaboration d’une suite d’opérations systématiques permettant, à partir d’une variété donnée, d’aboutir par diverses transformations birationnelles à une variété de référence. Cette variété de référence est, en un sens, la plus simple de sa famille, et peut servir de brique de base pour construire des variétés plus complexes. Dans son état d’avancement actuel, le programme minimal permet d’aboutir soit à une variété appelée modèle minimal, soit à une variété dite de Fano.
Les travaux récompensés par la médaille Fields
Caucher Birkar a obtenu la médaille Fields « pour sa preuve du caractère borné des variétés de Fano et pour des contributions au programme du modèle minimal1 ».
Caucher Birkar a participé à l’élaboration du programme du modèle minimal pour un type de variétés couvrant des cas importants, ce qui a contribué à faire du programme un outil essentiel. Par ailleurs, en prouvant le caractère borné des variétés de Fano, qui sont un des points d’arrivée du programme, il fait un apport crucial pour l’élaboration d’un programme du modèle minimal exhaustif.
-
En version originale : « for his proof of the boundedness of Fano varieties and for contributions to the minimal model program ».
↩
Alessio Figalli, spécialiste du transport optimal
Alessio Figalli est un mathématicien italien de 34 ans (en 2018) travaillant à l’École polytechnique fédérale de Zurich, principalement sur le calcul des variations et les équations différentielles aux dérivées partielles. Dit plus simplement, il s’intéresse à des équations qui décrivent des phénomènes dont les variations dans le temps et l’espace sont liées. Ces équations sont très importantes pour la physique notamment.
En particulier, Alessio Figalli travaille sur le transport optimal, qui lui a valu sa médaille Fields. Pour ceux que les mondanités intéressent, vous serez sûrement curieux d’apprendre qu’un de ses directeurs de thèse n’est autre qu’un des mathématiciens français les plus connus du grand public, Cédric Villani, également médaillé Fields (en 2010).

Qu’est-ce que la théorie du transport optimal ?
La théorie du transport optimal est le domaine des mathématiques qui s’intéresse aux moyens d’amener un système d’un état vers un autre à moindre coût. Dans les cas pratiques, ce coût peut être une énergie, une durée, un volume de carburant, etc.
Un des exemples de problème de transport optimal les plus anciens est énoncé par le mathématicien Gaspard Monge dans son Mémoire sur la théorie des déblais et des remblais en 1781. Il se pose la question suivante : comment déplacer des déblais afin de former un remblai pour un coût de déplacement minimal ? Autrement dit, comment se faire une fortification à partir d’un tas de terre en se fatiguant le moins possible ?
De nombreux problèmes peuvent être formulés sous une forme de problème de transport optimal. Par exemple, de nombreux systèmes physiques sont régis par des équations différentielles, dont les solutions peuvent aussi être vues comme la trajectoire d’un système cherchant à minimiser son énergie. C’est notamment le cas des équations semi-géostrophiques, dont les climatologues et météorologues se servent pour décrire les mouvements de l’atmosphère à grande échelle.
Les travaux récompensés par la médaille Fields
La médaille Fields lui a été remise « pour ses contributions à la théorie du transport optimal, ses applications aux équations aux dérivées partielles, à la géométrie des espaces métriques et aux probabilités1 ».
Grâce à ses travaux, notamment en collaboration avec De Philippis, on comprend désormais mieux les solutions des équations de Monge-Ampère, qui sont un type particulier d’équations aux dérivées partielles. Ces travaux ont des applications directes aux équations semi-géostrophiques.
Il est aussi récompensé pour des applications géométriques du transport optimal, en apportant une méthode plus générale que précedemment pour l’étude d’inégalités fondamentales telles que les inégalités isopérimétriques, mettant en relation l’aire d’une figure et son périmètre.
-
En version originale : « for his contributions to the theory of optimal transport, and its application to partial differential equations, metric geometry, and probability ».
↩
Peter Scholze, spécialiste de la géométrie algébrique arithmétique
Peter Scholze est un jeune chercheur en mathématiques de 30 ans (en 2018) de l’Université de Bonn, qui travaille à la frontière entre la théorie des nombres et la géométrie algébrique, ce qu’on appelle la géométrie algébrique arithmétique. Il s’intéresse ainsi aux liens entre les nombres entiers et certains objets géométriques.
Ses travaux se concentrent sur la géométrie algébrique arithmétique des corps p-adiques, domaine dans lequel il a introduit la notion d’espaces perfectoïdes. C’est un champ très pointu, dont il est difficile de donner une image simplifiée. Il est cependant possible de donner un avant-goût de la discipline en présentant les nombres p-adiques.

Qu’est-ce qu’un nombre p-adique ?
En théorie des nombres, les mathématiciens s’intéressent notamment à l’ensemble des entiers naturels , que l’on note . Parmi ces entiers naturels, les nombres premiers, ayant exactement deux diviseurs, un et eux-mêmes, jouent un rôle central. En particulier, chaque nombre entier peut être décomposé en un produit unique de nombres premiers, ce qui fait d’eux des « briques élémentaires » de la théorie des nombres.
Il existe d’autres types de nombres. On peut citer notamment :
- les entiers :
- les rationnels, c’est-à-dire les fractions :
- les réels : qui incluent en plus des rationnels tous les nombres que l’on ne peut pas exprimer comme une fraction de nombres entiers, comme , , ou .
Dans cette liste, et sont des corps. En bref, leur structure permet d’additionner, soustraire, multiplier et diviser.
La théorie générale permet de fabriquer des corps à partir d’autres en y ajoutant des éléments, tout en prenant soin de conserver de bonnes propriétés pour l’addition, la soustraction, la multiplication et la division. Notamment, pour un nombre premier fixé, on peut construire une extension du corps des rationnels , qu’on appelle alors corps des nombres -adiques, noté .
Pour mieux comprendre à quoi ressemble un nombre -adique, on peut se restreindre aux entiers p-adiques , ce qui revient à interdire les divisions. Un nombre de cet ensemble peut être représenté comme une suite de nombres entiers telle que pour tout , et . Dit plus simplement, un nombre entier tout bête est représenté par la suite des restes des divisions par pour n de plus en plus grand. Par exemple, le nombre est représenté par dans les entiers 2-adiques.
Comme on ne peut pas diviser, un élément de l’anneau ne possède pas nécessairement d’inverse multiplicatif. On construit alors le corps des fractions en les ajoutant.
Comme pour les nombres plus familiers (les entiers, les rationnels, les réels, etc.), on peut s’intéresser aux fonctions définies sur les p-adiques, à la convergence de suites, à la topologie… Ils fournissent un riche terrain de jeu et permettent par exemple de prouver des résultats sur les nombres entiers via différentes constructions.
Les travaux récompensés par la médaille Fields
Sa médaille Fields lui a été remise « pour avoir transformé la géométrie algébrique arithmétique sur des corps p-adiques par l’introduction des espaces perfectoïdes, avec application aux représentations galoisiennes et pour le développement de nouvelles théories de cohomologie1 ».
Cette médaille Fields récompense ses travaux révolutionnaires dans le domaine de la géométrie algébrique arithmétique. En particulier, sa notion d’espaces perfectoïdes a construit de nouveaux ponts entre géométrie et algèbre. Un de ses résultats les plus connus est la preuve d’une vieille conjecture concernant l’existence de représentations de Galois associées à des classes de torsion dans la cohomologie d’espaces localement symétriques.
Ses travaux sont très novateurs et captivants, comme en témoigne son éloge pour la médaille Fields : « La vision qu’a Scholze d’une théorie de la cohomologie sur les entiers est devenue une ligne directrice qui fascine la communauté mathématique dans son ensemble2 ».
-
En version originale : « for transforming arithmetic algebraic geometry over p-adic fields through his introduction of perfectoid spaces, with application to galois representations and for the development of new cohomology theories ».
↩ -
En version originale : « Sholze’s vision of a cohomology theory over the integers has become a guideline that fascinates the entire mathematical community ».
↩
Akshay Venkatesh, à la croisée des mondes
Akshay Venkatesh est mathématicien australien de 36 ans (en 2018) qui travaille à l’Université de Stanford, notamment sur la théorie des nombres, la théorie ergodique et les formes automorphes.
Il n’est pas aisé de décrire les travaux récompensés par la médaille Fields, tant ils sont divers et couvrent de nombreux champs des mathématiques. Sa médaille Fields lui a ainsi été remise « pour sa synthèse de la théorie analytique des nombres, de la dynamique homogène, de la topologie et de la théorie des représentations, qui a résolu des problèmes posés de longue date dans des domaines tels que l’équidistribution des objets arithmétiques1 ».

Ce qui est récompensé dans les travaux de Venkatesh, ce sont les liens qu’il a créés entre différents domaines des mathématiques, qui étaient jusqu’à présent insoupçonnés. En effet, la communauté mathématique apprécie les liens entre disciplines, comme celui assez ancien entre le monde des équations usuelles, l’algèbre, et celui des formes, la géométrie.
Ce qu’a réussi Venkatesh, c’est lier des domaines qui semblent fort éloignés au premier abord. Par exemple, il a lié la dynamique homogène, qui décrit des trajectoires à l’aide d’équations différentielles, à l’arithmétique, c’est-à-dire au monde des entiers naturels. Souvent, la portée de tels liens tend à chahuter la vision qu’ont les spécialistes des disciplines ainsi rapprochées.
À chaque fois qu’un mathématicien crée de nouveaux liens entre sujets, la vision des mathématiques comme un tout cohérent est renforcée. Il existe une fascination pour la manière dont tous les concepts s’agencent, que chaque pont inattendu entre deux univers intensifie. Pour certains, ces surprises font des mathématiques la plus belle des sciences.
-
En version originale : « for his synthesis of analytic number theory, homogeneous dynamics, topology, and representation theory, which has resolved long-standing problems in areas such as the equidistribution of arithmetic objects ».
↩
Références
- La page des médailles Fields 2018 sur le site de l’IMU.
- Portrait de Caucher Birkar sur la chaîne Youtube de l’ICM 2018.
- Portrait de Peter Scholze sur la chaîne Youtube de l’ICM 2018.
- Portrait de Alessio Figalli sur la chaîne Youtube de l’ICM 2018.
- Portrait de Akshay Venkatesh sur la chaîne Youtube de l’ICM 2018.
Merci à @qwerty pour la validation et à @Vayel pour sa relecture lors de la bêta.





