Quelle est la probabilité de couper sur la fève ?

Pour calculer des probabilités, il faut d’abord bien définir le problème que l’on cherche à résoudre. Autrement, il sera impossible d’utiliser des outils mathématiques pour le résoudre. Nous voulons pouvoir traiter mathématiquement les trois éléments essentiels du problème : la galette, la fève et la découpe.

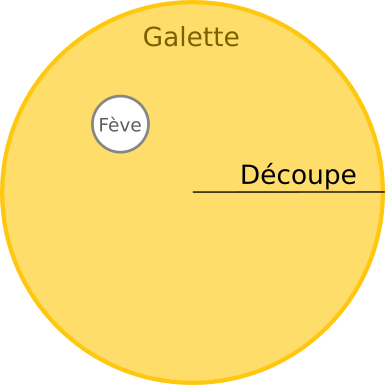
Assimilons une galette à un disque de rayon $D$. Cette hypothèse est assez bien vérifiée en pratique, pour peu que le pâtissier soit habile et attaché aux traditions.

Ensuite, considérons que la fève est aussi un disque, de rayon $d$. Physiquement, il faut que le rayon de la fève soit plus petit que celui de la galette pour tenir à l’intérieur. En vérité, ce n’est pas la forme de la fève qui importe, comme nous le verrons.

Enfin, considérons qu’une découpe est un rayon de la galette ; autrement dit, un segment qui relie le centre au bord.

Les lecteurs avides de rigueur sont invités à traiter les cas exotiques dans les commentaires :

• galettes ovales, rectangulaires ou informes ;
• plusieurs fèves ;
• découpes non conventionnelles.

Je me contenterai de m’occuper des choses les plus traditionnelles.

Calcul de la probabilité

La probabilité d’un événement, c’est tout simplement le ratio du nombre de situations dans lesquelles l’événement se produit et du nombre total de situations.

$P = \frac{\text{nombre de situations avec l'événement}}{\text{nombre total de situations}}$

Dans notre cas, on souhaite connaître la probabilité de l’événement « couper sur la fève ». Il nous faut donc déterminer le nombre de situations dans lesquelles on coupe sur la fève ainsi que le nombre total de situations (celles dans lesquelles on tombe sur la fève, ou pas). On ne peut pas compter les manières de découper comme on compterait des pièces de monnaies, car il y en a un nombre infini. Le « nombre » de situations correspond en fait à la taille d’un secteur du disque. Autrement dit, il s’agit d’un angle.

Les situations où on coupe sur la fève sont celles où la découpe tombe dans le secteur de la galette occupé par la fève. Le « nombre » de telles situations est donc la taille angulaire du secteur occupé par la fève. On voit ici que la forme exacte de la fève importe peu, seulement l’angle occupé. On notera $f$ cet angle.

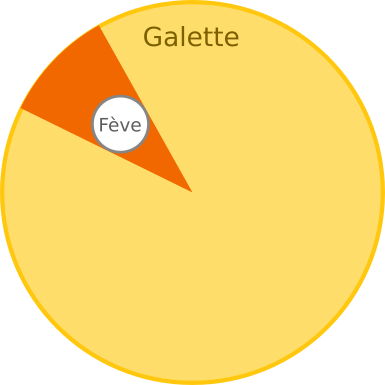
Le nombre total de situations est encore plus simple : il s’agit de toutes les manières possibles de faire une découpe dans la galette. Le secteur occupé par la galette est un disque complet et correspond donc à un angle de 360°.

Ainsi, la probabilité de tomber sur la fève pour une seule découpe est :

$P = \frac{\text{nombre de situations avec l'événement}}{\text{nombre total de situations}} = \frac{f}{360°}~.$

Exemple

Reprenons notre galette idéale schématisée avant. Le secteur occupé par la fève mesure environ 34°, mesuré numériquement avec mon logiciel de dessin.

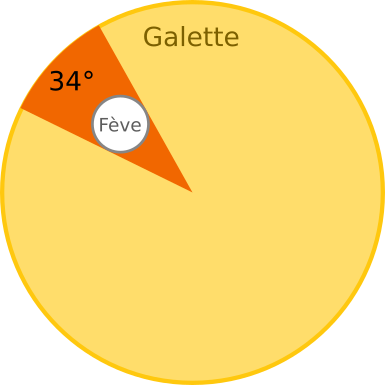
La fève occupe environ 34°. La probabilité de tomber sur la fève est donc de :

$P = \frac{34°}{360°} \approx 0{,}094$

Autrement dit, il y a un peu moins d’une chance sur 10 de tomber sur la fève.

Conseils aux pâtissiers

Pour limiter les cas de découpe sur la fève, on conseillera de réduire le secteur angulaire de la fève :

• en la plaçant le plus au bord possible (tout en restant dans la galette évidemment) ;
• en réduisant sa taille (pas trop petite non plus, pour ne pas la manger par accident) ;
• ou encore en choisissant une forme fine, telle un bâtonnet étroit, qu’on placerait radialement.

La situation pour une découpe n’est cependant qu’une maigre information, puisqu’il y a besoin d’en faire plusieurs pour faire des parts.

Remarques préliminaire

Pour simplifier, nous ne considérons que des parts égales. Dans ce cas-là, il faut autant de découpes que de parts, comme le montre l’exemple ci-dessous.

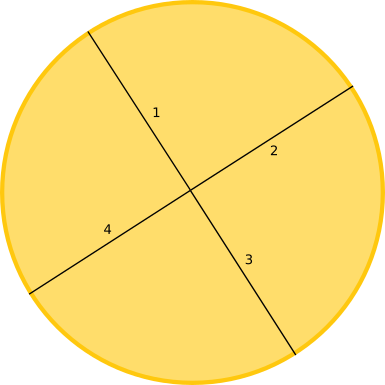
Aussi, pour peu que la fève soit assez grosse (angulairement) ou le nombre de parts assez grand, on coupe à coup sûr sur la fève. En effet, la fève occupera alors un secteur angulaire plus large qu’une part. Cette situation correspond à une probabilité de 1 de couper sur la fève.

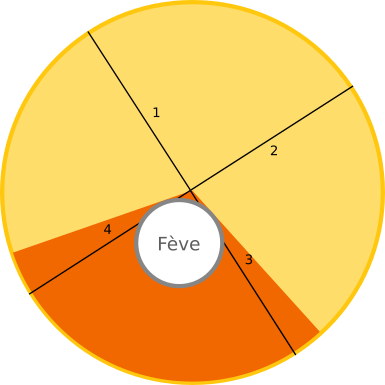
Découpe dans un secteur virtuel

On constate que, dans le cas de parts égales, la première découpe définit toutes les parts suivantes. Aussi, il n’y a que la position de la première découpe qui ait en fait une importance.

Par ailleurs, comme toutes les parts sont identiques, il est toujours possible de considérer que la première découpe se fait dans un secteur « virtuel » de la largeur d’une part qui contient la fève entièrement (voir schéma ci-dessous). Si ce n’était pas le cas, alors ce serait en pratique le cas pour un autre secteur virtuel. Il est aussi toujours possible de choisir un tel secteur virtuel quand on n’est pas dans le cas des parts plus fines que la fève.

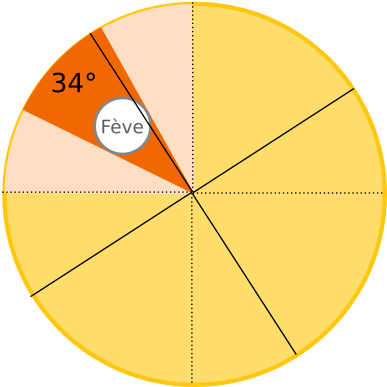
Ainsi, on considère la probabilité avec les nombres de situations suivants :

• un secteur d’angle $f$ pour tomber sur la fève ;
• un secteur d’angle $\frac{360°}{n}$ pour faire une découpe.

On obtient la probabilité suivante :

$P_n =\frac{f}{\frac{360°}{n}} = \frac{n \cdot f }{360°}~.$

On a exclu les cas de probabilité 1. On peut les réintégrer en utilisant un minimum pour éviter de dépasser 1, ce qui se traduit par :

$P_n = \min \left(\frac{n \cdot f}{360°} ; 1 \right).$

Placement de la fève a posteriori

On peut aussi voir le problème sous un autre angle. On fait $n$ découpes pour faire les $n$ parts, et on met la fève à un endroit donné ensuite, comme si on remontait le temps.

Dans une telle situation, pour chaque découpe, si on repère la fève par son centre, celle-ci se trouve sous la découpe seulement si son centre se trouve dans un secteur de largeur $f$. Comme on a un tel secteur par découpe, on fait la somme des $n$ zones où la fève tomberait sous la découpe et on retrouve la formule donnée avant :

$P_n = \frac{n \cdot f}{360°} ~.$

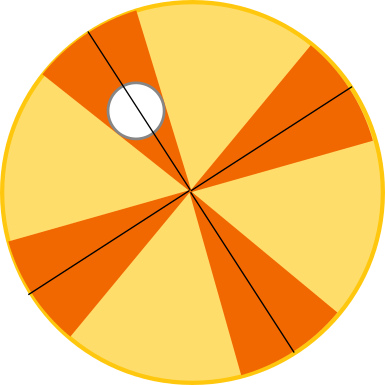
Dans le cas de la fève large, ces secteurs se rejoignent pour occuper toute la galette et on ne peut pas les additionner sans précaution. À partir du moment où les angles se rejoignent, la probabilité vaut 1 et n’augmente plus. Pour prendre ce cas en compte, il suffit de prendre le minimum de la probabilité calculée avant et de 1 :

$P_n = \min \left(\frac{n \cdot f}{360°} ; 1 \right).$

Exemple

Si on calcule ce que la formule donne pour une découpe en 6 avec la fève de 34° prise précedemment, on obtient :

$P_6 = \min\left(\frac{6 \cdot 34°}{360°}; 1\right) \approx 0,57.$

Soit plus d’une chance sur deux de tomber sur la fève !

Résumé en image

Pour bien fixer les idées, quoi de mieux qu’un diagramme ! Comme ça, vous savez immédiatement la probabilité que vous avez de tomber sur la fève, pour peu que vous connaissiez sa taille et le nombre de parts. La figure ci-dessous est obtenue à partir de la formule pour $P_n$ en la calculant pour différentes valeurs de $n$ et $f$.

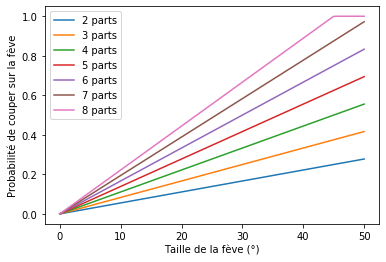
Conseils aux découpeurs de galette

Comme on le voit ici, plus le nombre de parts augmente, plus il est probable de couper sur la fève. On conseillera donc aux personnes mangeant de la galette de la manger seule, ce qui minimise les chances de couper sur la fève et maximise les chances d’être le roi ou la reine !