Démontrer la loi de Snell-Descartes

Explication

Pour faire de l’optique géométrique, on suppose plusieurs choses sur la lumière :

• il n’y a pas de phénomène de diffraction.
• les rayons sont indépendants les uns des autres.
• et le principe de Fermat

Le postulat qui nous intéresse ici est celui de Fermat, que l’on appelle aussi principe de moindre temps. Il stipule qu’entre deux points A et B, atteints par la lumière, le chemin optique suivi le long du trajet est extrémal. Le chemin optique, entre A et B, est défini comme :

$L(AB) = \int_A^B n(s) \mathrm ds$ Avec $ds$ l’abscisse curviligne et $n(s)$ l’indice de réfraction

On peut interpréter le chemin optique comme le trajet que parcourrait la lumière si le trajet se faisait dans le vide.

Dans le cas des milieux homogènes, le chemin optique devient : $L(AB) = n \int_A^B \mathrm ds = AB \times n$

Le principe de Fermat impose que le trajet entre A et B soit minimal, et le moyen le plus court pour relier deux points c’est une droite. On a donc démontré que la lumière se déplace en ligne droite dans un milieu homogène.

Illustration

Pour illustrer le principe de Fermat, prenons un exemple, supposons que la lumière va du point A au point B, en changeant de milieu. On sait que la lumière va se déplacer en ligne droite, mais on a "plusieurs chemins possibles" :

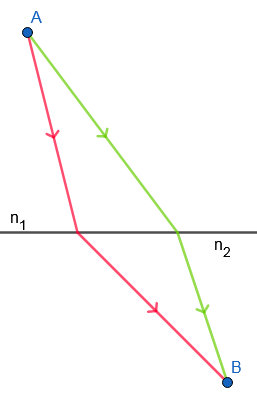
Le principe de Fermat nous dit que le chemin choisi va être celui qui prend le moins de temps.

Calcul du temps de parcours

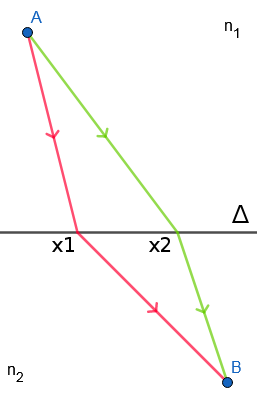
Si on regarde ce schéma, on a deux points A et B fixés qui sont dans deux milieux différents, on considère que la lumière passe par ces deux points, la question que l’on peut se poser alors : en quel point de la droite $\Delta$ la lumière va changer de milieu.

On introduit ensuite une base $(\vec{e_x}, \vec{e_y})$ sur le point A. On note $(x_b, y_b)$ les coordonnées sur point B et $(x_o, y_o)$ celle du point O, dans cette base.

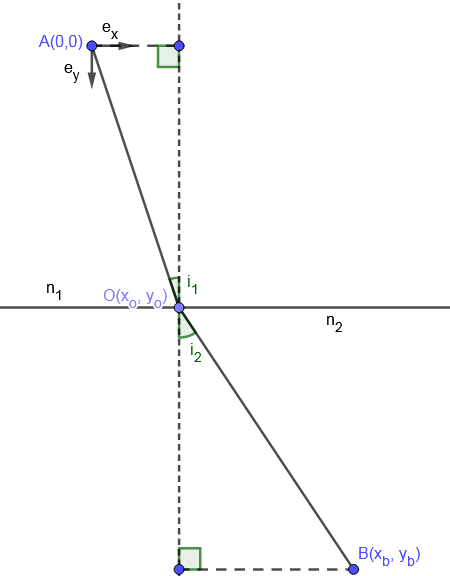
La distance parcourue correspond à $AO + BO$. De plus, on a $AO = \sqrt{x_o^2 + y_o^2}$ et $BO = \sqrt{(x_o - x_b)^2 + (y_o - y_b)^2}$.

Le temps mis par la lumière est donc $t = \frac{AO}{v_{AO}} + \frac{BO}{v_{BO}}$. L’indice de réfraction nous donne que $v_{AO} = \frac{c}{n_1}$ et $v_{BO} = \frac{c}{n_2}$ Donc

$\boxed{t = \frac{n_1 \sqrt{x_o^2 + y_o^2}}{c} + \frac{n_2 \sqrt{(x_o - x_b)^2 + (y_o - y_b)^2}}{c}}$

On veut que $t$ soit le plus petit possible, et pour trouver le minimum d’une fonction, on calcule la dérivée.

Calcul des dérivées

Si on regarde l’expression de $t$, on peut voir qu’elle dépend de plusieurs paramètres : $x_o$, $y_o$, $x_b$ et $y_b$. Déjà, on sait que la position du point A et B sont fixés donc $x_b$ et $y_b$ sont connus. De plus le point O est à l’interface entre les deux milieux, d’où le fait qu’on connaisse sont ordonnée $y_o$.

Donc $t$ est une fonction de paramètre $x_o$. On peut alors calculer la dérivée :

$t'(x_o) = \frac{n_1 \times 2x_o}{c \times 2\sqrt{x_o^2 + y_o^2}} + \frac{n_2 \times (2x_o - 2x_b) }{c \times 2\sqrt{(x_o - x_b)^2 + (y_o - y_b)^2}}$ $t'(x_o) = \frac{n_1 \times x_o}{c \times \sqrt{x_o^2 + y_o^2}} + \frac{n_2 \times (x_o - x_b) }{c \times \sqrt{(x_o - x_b)^2 + (y_o - y_b)^2}}$

On calcule ensuite la dérivée seconde :

Après simplification :

On peut voir que celle-ci est positive.

Résultat final

Si on reprend le schéma, on a deux triangles rectangles donc : $\sin(i_1) = \frac{x_0}{\sqrt{x_o^2 + y_o^2}}$ et $\sin(i_2) = \frac{x_b - x_o}{\sqrt{(x_o- x_b)^2 + (y_o - y_b)^2}}$

En injectant cela dans la formule de la dérivée : $t'(x_o) = \frac{n_1 \times \sin(i_1)}{c} - \frac{n_2 \times \sin(i_2)}{c}$

De plus $t''(x_o)$ est positive donc $t(x_0)$ admet un minimum lorsque $t'(x_o) = 0$, on obtient alors : $0 = \frac{n_1 \times \sin(i_1)}{c} - \frac{n_2 \times \sin(i_2)}{c}$ D’où $\boxed{n_1 \times \sin(i_1) = n_2 \times \sin(i_2)}$

On a bien démontrer la deuxième loi de Snell-Descartes.