Le théorème Pi et Pythagore

Une preuve originale du plus célèbre des théorèmes

Qui ne connait pas le théorème de Pythagore ? (Si vous etes déjà perdu faite un tour ici ) Les preuves les plus classiques sont présentées dans le lien précédant, mais j’aimerai vous présenter "ma préférée" , qui repose sur le Théorème de Vaschy-Buckingham , surnommée "Théorème $\Pi$ "(vous devinerez vite pourquoi).c’est un théorème fondamental pour l’analyse dimensionelle et l’homogénéité en physique , mais il peux servir à bien d’autre chose ;)

Le Théorème de Vaschy-Buckingham

Le Théorème $\Pi$

Fondement

Le théorème $\Pi$ repose sur un des fondements de la physique :

Les lois de la physiques sont invariantes par changement d’unité.

Il en résulte que toute loi physique doit pouvoir s’exprimer en fonction de variables sans dimension (sans unité) .

Une grandeur dimensionnée est une variable ( temps , masse , longueur , vitesse ,etc…) ou bien une constante universelle ($c,g,\epsilon_0, h ... $)

Énoncé

Pour un problème physique comportant :

  • $N$ grandeurs dimensionnées
  • $P$ dimensions indépendantes

On peut définir $n=N-P$ variables sans dimensions qu’on note $\pi_1 ,...,\pi_n$ Les lois physique qui le régisse se mettent sous la forme : $f(\pi_1 ,...,\pi_n) = 0 $

Le théorème de Pythagore

Présentation du Problème

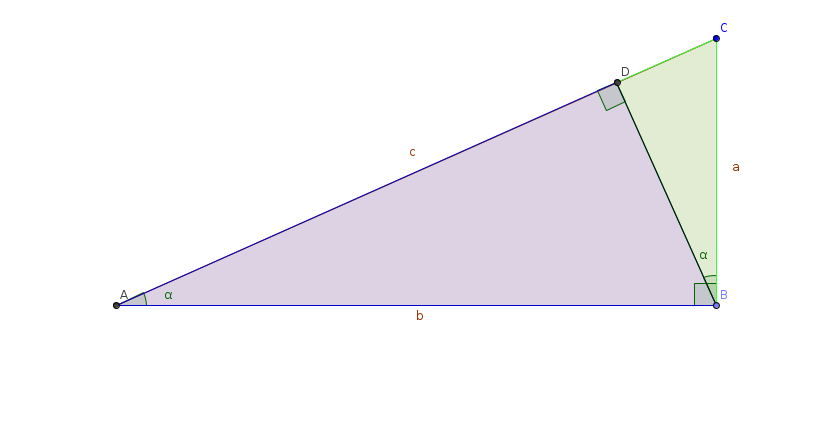
Le triangle rectangle étudié , la source de notre "problème physique"

Déterminer l’aire du triangle ABC constitue un problème (physique) .

On dispose de :

  • 3 grandeurs indépendantes : $\mathcal{A}$ (l’aire du triangle en m²) , $c$ longueur de l’hypothénus ,en m) et $\alpha$ l’angle en A (sans dimension par convention) .
  • 1 dimension indépendante: la longueur. (avec le mètre comme unité , mais le mile nautique ou la taille de votre pied peux tout aussi bien servir )

Preuve

D’après le théorème $\Pi$ on peut trouver $\pi_1$ et $\pi_2$ sans dimension dans notre problème tel que : $f(\pi_1,\pi_2) = 0 $ où encore $\pi_1= g(\pi_2)$ (l’existence de g est assurée par le théorème des fonctions implicites)

on choisit donc :

$$ \begin{aligned} \pi_1 &= \frac{\mathcal{A}}{c^2} \\ \pi_2 &= \alpha \end{aligned}$$

Alors on a

$$ \begin{aligned} \frac{\mathcal{A}}{c^2} &= g(\alpha) \\ \mathcal{A} &= c^2 g(\alpha) \\ \end{aligned} $$

En notant $\mathcal{A}_1$ l’aire du triangle ADB et $\mathcal{A}_2$ l’aire du triangle BCD , on retrouve le même problème et donc la même loi physique. :

$$ \begin{aligned} \mathcal{A}_1 &= b^2 g(\alpha) \\ \mathcal{A}_2 &= a^2 g(\alpha) \\ \end{aligned} $$

Or on a :

$$ \begin{aligned} \mathcal{A}_1 +\mathcal{A}_2 &=\mathcal{A} \\ b^2 g(\alpha) + a^2 g(\alpha) &= c^2 g(\alpha) \\ \end{aligned} $$ En simplifiant par $g(\alpha)$ , non nul ( si c'était le cas on aurait $\mathcal{A} = 0$ ) il vient alors : $$ a^2 + b^2 = c^2 $$

On a redémontré le théorème de Pythagore !

Pour en savoir plus :

Le théorème $\Pi$ et sa preuve.

Merci d’avoir lu jusqu’ici mon premier billet :)

11 commentaires

En voila une belle preuve qui change des découpages astucieux. Elle deviendra ma preuve préférée quand je me serai débarassé de deux doutes.

  1. L’aire d’une triangle rectangle peut réellement être exprimée comme fonction de la longueur de l’hypoténus et de l’angle. (il faut que je réactive ma géométrie dans le cercle)

  2. Le théorème dit qu’il existe des grandeurs pi1 et pi2 et une fonction f telle que f(pi1,pi2)=0. Il ne dit pas qu’une telle fonction existe quel que soit le choix de pi1 et pi2.

Le second point se règle, je crois en disant que tous les choix possibles sont "proportionnels" au sens des exposants. C’est ce que dit sans le dire l’article de Wikipédia qui dit que les variables sans dimension s’expriment comme des monômes en les autres variables.

+0 -0

Je suis d’accord avec LaurentClaessens sur son deuxième point. Je n’ai pas lu l’article Wikipédia, mais je trouve qu’il y a un problème dans le passage de l’enoncé du théorème à la preuve de celui de Pythagore. Aussi, je suppose que le passage avec les fonctions implicites est très ’physicien’ (je me permets l’expression vu le billet) à la mode "nos fonctions sont toujours gentilles", non ?

+3 -0

pour moi la puissance de cette preuve et ( et de ce théorème) c’est qu’on n’a pas a déterminer ni $f$ ni $g$ . Pour etre rigoureux et appliquer le théorème des fonctions implicites il faut que $f$ soit au minimum $\mathcal{C}^1$ , et j’avoue n’avoir aucune idée pour le démontrer.

Quand on m’a présenter cette preuve c’était en cours de physique (où toutes les fonctions sont "gentilles" comme le présentait Kanaal) et du coup ca ne m’a pas posé problème jeunes et insouciant que j’était :ange: .

+0 -0

Non il ne suffit pas que f soit différentable. Il faut un peu plus que ça, et sans connaître sa forme ce n’est pas possible d’en conclure.

À mes yeux ce n’est pas tellement une preuve, puisque les hypothèses contiennent directement la conclusion, mais plutot une sorte de confirmation ou d´exercice

+1 -0
Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte