Les deux volets précédents ont traité respectivement des méthodes utilisées durant l’Antiquité et le Moyen Âge (vous pouvez le trouver ici) et puis durant les Temps modernes (que vous pouvez trouver ici). Ces périodes étant terminées, il nous faut encore traiter l’Époque contemporaine, celle dans laquelle nous nous trouvons actuellement. Il faut noter que les méthodes ayant fortement évolué (entre autres grâce à l’apparition des ordinateurs), elles sont devenues plus complexes à expliquer ainsi qu’à comprendre. Mais rassurez-vous, nous avons pris soin de les simplifier autant que possible, car le but de cette mini-série d’articles est de tracer un tour d’horizon des méthodes employées et non de faire un cours complexe sur leur fonctionnement.
Bonne lecture !
Jusqu’ici, les chiffrages étaient bien souvent faits à la main. Mais vers l’an 1800, on se rapproche des systèmes mécaniques, voire électroniques ! Nous allons maintenant voir une énorme amélioration due au bout d’un moment à la puissance des machines mises à la disposition de l’Homme pour faire ce qu’il n’était plus capable de faire seul sur un (ou plusieurs) papier(s).
- Le cylindre de Jefferson
- Le Playfair de Wheatstone
- Avancée du décryptage
- Le masque jetable de Vernam
- Enigma de Scherbius
- DES
- RSA
- La cryptographie quantique
- PGP de Zimmerman
- Sources et liens
Le cylindre de Jefferson
Thomas Jefferson, le ─ pas encore à l’époque ─ président des États-Unis d’Amérique a inventé dans les années 1790 un système qui porte son nom. Ce système a pour nom complet le Cylindre de Jefferson. Avec un nom pareil, vous vous doutez bien qu’il va être question d’un cylindre, mais qu’y a-t-il dans ce cylindre ? Ce cylindre est composé de 26 disques rotatifs sur lesquels sont inscrites les 26 lettres de l’alphabet dans un ordre aléatoire (tel qu’il n’y ait pas deux disques identiques). Il y a 26 disques pour une raison purement arbitraire. Voici sur l’image qui suit un exemple de cylindre.
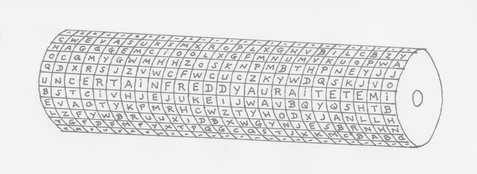
Sur cette image, vous pouvez voir, au centre, un message : "UN CERTAIN FREDDY AURAIT ETE MI…". Le message ne sait être plus long car le cylindre n’a que 26 disques donc 26 lettres chiffrées dans le message. Cependant, rien n’empêche de recommencer une seconde phrase commençant par le premier caractère qui n’a pas pu être écrit auparavant.
Maintenant que le message à chiffrer est écrit, il nous faut le chiffrer. Pour ce faire, il nous suffit de récupérer les lettres écrites juste en dessous du message. Ici en l’occurrence, le message chiffré est le suivant : "BSTCIVHJEJUKEIJWAVBQYQSHTB". Il faut ensuite envoyer ce message-ci au destinataire qui doit avoir sensiblement le même outil que vous sinon il sera incapable de déchiffrer le message. Le destinataire qui tente de déchiffrer le message recopie ce qu’il a reçu sur son propre cylindre et cette fois-ci ne regarde pas la ligne du dessous comme fait pour chiffrer mais bien la ligne du dessus. En faisant cela, il retombera exactement sur le même message. Et là vous comprenez quel est l’intérêt d’avoir le même cylindre. S’il avait les lettres écrites dans un ordre différent sur un des disques, le destinataire aurait été dans l’incapacité de comprendre ce qui lui a été envoyé. Pareil si ses disques ne sont pas placés dans le même ordre. Pour les matheux, vous remarquerez vite qu’avec 26 cylindres à placer, on a (lire factorielle de 26) permutations possibles. Et , ça fait . Il y a donc bon nombre de dispositions possibles pour les cylindres. Il y en a tout autant pour l’ordre des lettres sur chaque disque. Et si on veut combiner les deux, vous comprendrez qu’il est impossible de déchiffrer le message sans avoir la machine…
Ce système n’a pas été utilisé pendant longtemps par Jefferson, mais a été repris par (entre autres) l’armée américaine pendant la seconde guerre mondiale dans une version améliorée et adaptée.
Le Playfair de Wheatstone
Dans les alentours de 1850, Sir Charles Wheatstone invente un nouveau système inspiré des rectangles de substitution. Son système est simple : il part d’une table contenant les 26 lettres de l’alphabet sans le J qui est fusionné avec le I (l’utilisation de la langue française préfère enlever le W et le fusionner avec le V pour garder I et J séparés). Voici un exemple de table que l’on peut utiliser.
B | O | V | Y | C |
E | T | M | F | P |
Q | S | K | U | J |
R | I | A | X | L |
G | D | H | N | Z |
À partir de ce tableau, il nous faut un message à chiffrer mais il ne nous faut pas de clé : la clé est notre tableau1. Vous avez fort probablement deviné quel est le message que nous allons chercher à chiffrer, alors chiffrons-le ! Prenons notre message "ZESTEDESAVOIR" et commençons par le découper par blocs de deux lettres. Notre message devient donc "ZE" "ST" "ED" "ES" "AV" "OI" "R". Ici, on a un problème. Contrairement au cadran d’Alberti, ici il nous faut que chaque bloc fasse 2 lettres, pas une de plus et pas une de moins. On va donc ajouter ce qu’on appelle des nulles dans le jargon. Ce sont des caractères qui nous servent à faire rentrer notre message dans les cases qu’on lui propose. On peut également parler de padding. Ici, comme il nous manque une lettre nous allons rajouter un seul caractère. On utilise habituellement des caractères non alphabétiques (voire non imprimables) pour faire des nulles mais ici, on est obligés de prendre des lettres car c’est tout ce qu’il y a dans notre tableau. Alors on rajoute des caractères peu utilisés tels que le X ou le Z. Nous allons utiliser un X car on a déjà un Z dans notre message initial, donc afin de ne pas s’embrouiller, on rajoute un caractère n’étant pas déjà apparu2. Maintenant que nous avons découpé notre message, il nous faut trouver les caractères chiffrant. Il faut savoir que nous allons chiffrer chaque couple de caractère par un autre couple (donc notre nulle sera chiffrée également). Pour savoir quelles lettres vont chiffrer quelles lettres, il faut connaître les 3 règles déterminées par Wheatstone. Les voici :
- si les deux caractères à chiffrer se trouvent sur la même colonne, ils seront chiffrés respectivement par le caractère d’en dessous de chaque caractère du couple ;
- si les deux caractères à chiffrer se trouvent sur la même ligne, ils seront chiffrés respectivement par le caractère de droite de chaque caractère du couple ;
- si les deux caractères à chiffrer forment un rectangle, ils seront respectivement chiffrés par le coin opposé du rectangle se trouvant sur la même ligne que le caractère.
Donc, commençons à chiffrer. On commence avec le couple (’Z', 'E’) qui forme le rectangle EPZG. On regarde donc les côtés opposés P et G en commençant par le caractère sur la ligne du Z puis celui sur la ligne du E ce qui nous donne "ZE" -> "GP". On fait pareil avec "ST" qui est successivement sur la seconde colonne. On prend donc le caractère en dessous de S (à savoir I) et le caractère en dessous de T (à savoir S) et on les ajoute à notre message chiffré, ce qui nous donne "ZEST" -> "GPIS". Nous vous laissons continuer jusqu’à la presque fin : vous devez obtenir "ZESTEDESAVOI" -> "GPISTGTQHMTD". Reste le dernier couple (’R', 'X’) qui se fait exactement de la même manière. On les trouve (sur la 4e ligne), puis on suit la règle qui nous dit qu’on doit prendre les caractères à droite (à savoir I et L). Maintenant, nous avons fini de chiffrer et on a obtenu "ZESTEDESAVOIR(X)" -> "GPISTGTQHMTDIL".
Nous ne vous avons pas expliqué pourquoi on parlait du Playfair de Wheatstone. C’est parce que Wheatstone a inventé un procédé qui a été repris et popularisé par le baron Lyon Playfair d’Écosse. C’est une fois de plus le mauvais nom qui est associé à une méthode.
Avancée du décryptage
Vers 1850, le mathématicien britannique Charles Babbage casse pour la première fois le chiffre de Vigenère mais garde bien précieusement son information pour lui. Elle n’a été retrouvée que 100 ans plus tard dans ses écrits par hasard. Quelques années après, vers 1860, Friedrich W. Kasiski, un officier prussien (de l’actuelle Pologne), publie un livre consacré à la cryptanalyse1 des chiffrements polyalphabétiques. Ça vous dit quelque chose les chiffrements polyalphabétiques ? C’est normal, c’est ce que l’on a vu précédemment avec Trithème. Donc ce qu’on appelle le chiffre de Vigenère (et ses dérivés) ! Et attention, 30 ans plus tard, c’est Étienne Bazeries, l’officier français qui réussit pour la première fois à casser (pas entièrement, mais une bonne partie) le Grand Chiffre des Rossignol. La cryptanalyse a pris un bon pas sur la cryptographie pendant ce demi-siècle là. Mais qu’à cela ne tienne, quand il y a un manque de moyen sûr pour chiffrer des informations parce que les chiffrements polyalphabétiques (les plus utilisés jusque là) ont été cassés, on les améliore !
-
À ne pas confondre avec la cryptographie, la cryptanalyse est la science qui cherche à casser les algorithmes ou du moins les méthodes trouvées par cette dernière.
↩
Le masque jetable de Vernam
En 1917, Gilbert Stanford Vernam, un ingénieur américain travaillant aux laboratoires de l’actuelle très célèbre firme AT&T a trouvé un fonctionnement (théorique) infaillible pour pouvoir utiliser les chiffrements polyalphabétiques sans risque. Ce principe s’appelle le principe du masque jetable. Ça veut bien dire ce que ça veut dire : on utilise un masque qu’on jette, qu’on ne réutilise plus jamais. Ce masque doit par contre être de longueur égale au texte pour ne pas qu’il y ait de répétitions des caractères de la clé. Si ce masque est généré aléatoirement d’une longueur égale à celle du texte et n’est plus jamais réutilisé, alors votre message est parfaitement sécurisé, il n’y a pas d’autre moyen que le brute-force1 pour le déchiffrer.
Ce n’est donc pas un nouveau procédé, c’est uniquement une nouvelle analyse des chiffres existant pour en tirer ce qu’ils ont d’optimal.
-
Le brute-force est le fait d’essayer toutes les possibilités. C’est faisable si vous désirez coder un court message (tel que "ZESTEDESAVOIR" par exemple…
↩ ) mais devient compliqué si vous comptez chiffrer tout un document écrit par un agent de la NSA.
) mais devient compliqué si vous comptez chiffrer tout un document écrit par un agent de la NSA.
Enigma de Scherbius
La machine Enigma a été conçue dans les années 1910 en Allemagne par Arthur Scherbius et a été commercialisée dans les années 1920. Elle est très connue, car elle a servi au chiffrage des messages de l’Allemagne nazie pendant la Seconde Guerre mondiale (et a été déchiffrée par plusieurs équipes de mathématiciens dont celle du célèbre logicien britannique Alan Turing).
Enigma est une machine électromécanique. C’est-à-dire qu’elle est composée d’une association de pièces électroniques et de pièces totalement mécaniques (c’était ça les années 1920 !). Le fonctionnement interne est un peu compliqué à décrire en détail, mais le tout est basé sur un principe de rotors rotatifs. Pour commencer, voici une image (c’est une miniature étant donné que l’image est très grande, cliquez pour la voir en grand).
Vous pouvez donc voir que nous avons subdivisé (avec de magnifiques talents graphiques) cette machine en 4 parties à savoir ROTORS, TABLE DE RÉSULTATS, CLAVIER et TABLE DE BRANCHEMENTS.
Tout d’abord, il faut mettre la machine dans une configuration initiale (et il faut que le destinateur et le destinataire aient exactement la même !) dépendant des rotors et de la table de branchements. Cette table de branchement n’existait pas sur la version initiale (inventée par Scherbius) mais a été rajoutée par les Allemands pendant la Deuxième Guerre mondiale. Son principe est simple : elle sert à brouiller le message encore plus en substituant une lettre par une autre. On l’appelle table de branchements, car il faut brancher 10 paires de lettres (oui oui, donc 20 lettres) pour pouvoir changer l’une par l’autre dans le message final. Pour terminer la configuration initiale, il faut aussi placer les rotors dans un certain état. Ces trois rotors ont chacun les 26 lettres associées dans un ordre particulier1 (un peu comme le Cylindre de Jefferson). Le nombre d’arrangements possibles en comptant ces trois rotors est de . S’il y a 60 possibilités pour les placements des rotors, il y en a beaucoup plus pour les branchements ! La formule est un peu compliquée mais la voici. S’il y a 26 lettres pouvant être connectées 2 par 2 (tel que A-B = B-A) et qu’on veut faire 10 paires, le nombre de branchements possibles est le suivant : . Le nombre total d’états initiaux possibles pour la machine correspond à la multiplication de ces trois résultats : . Donc peut-on considérer Enigma comme une machine sûre si seul vous connaissez la position initiale de la machine ? À moins que vous connaissiez quelqu’un capable de tester les presque possibilités en un temps acceptable. À priori, on peut dire que c’est relativement sûr2.
Maintenant que nous vous avons fait peur avec ces formules mathématiques, nous allons vous expliquer comment fonctionne cette machine. La machine étant dans son état initial, il ne vous reste plus qu’à écrire. Donc quand vous pressez la touche Z du clavier, un signal passe la table de permutations, change le Z en la lettre qui lui est associée, et puis envoie cette même lettre aux rotors. La lettre subit une suite de modifications en passant par les trois rotors (de droite à gauche). À ce moment-là, la lettre et renvoyée dans les rotors (mais de gauche à droite cette fois-ci). Elle re-subit donc des modifications. Une fois les rotors passés, la lettre est renvoyée sur la table de branchements pour la re-changer. Et seulement après cela, elle est envoyée sur la table de résultats pour afficher (à l’aide d’une ampoule) la lettre chiffrée. Et une fois ce cycle fait, le rotor de droite (appelé rotor rapide) tourne d’un cran. Une fois que ce rotor a fait un tour (donc qu’il revient à sa position nulle, la première lettre), le second rotor (appelé rotor normal) se décale d’un cran. Et bien entendu, quand ce dernier termine son tour, il fait tourner le dernier rotor (appelé rotor lent). Le chemin parcouru par le signal est donc CLAVIER -> TABLE DE BRANCHEMENTS -> ROTORS -> RÉFLECTEUR -> ROTORS -> TABLE DE BRANCHEMENTS -> TABLE DES RÉSULTATS. Une fois le résultat affiché sur la machine, il était recopié sur un papier, et à la fin, quand tout le message est chiffré, c’est ce code-là qui est transmis pour être déchiffré.
Pour déchiffrer, ils faisaient exactement la même chose : ils mettaient la machine dans le même état initial que l’envoyeur, puis ils appuyaient sur chaque touche du message chiffré dans l’ordre. Par exemple, si "ZESTEDESAVOIR" avait été chiffré en "DIKQMAPHRIST" (ce qui est possible car deux lettres du message clair pouvaient donner deux lettres différentes dans le message codé, et deux lettres identiques du message codé ne correspondaient pas obligatoirement à deux lettres identiques du message clair), les déchiffreurs devaient agir comme s’ils voulaient chiffrer "DIKQMAPHRIST" et ils obtiendraient le message initial.
Vous vous demandez peut-être comment les Allemands faisaient pour savoir dans quel état initial mettre leur machine pour déchiffrer. Effectivement, ils n’allaient pas tester les milliards de milliards de possibilités sinon on perd tout l’intérêt de la cryptographie. Ils avaient des tables pour chaque jour de chaque mois avec une information concernant les rotors à prendre et l’ordre dans lequel les placer, la valeur initiale à donner à chaque rotor, les branchements à faire, etc.
Comme dit plus haut, ce système a été cassé à cause d’une défaillance (ou plutôt d’une faiblesse) de la machine : une lettre ne sera jamais chiffrée par elle-même. Ça peut vous paraître anodin, mais c’est très important car les Américains, Britanniques, Français, … s’en sont servi. Ils cherchaient un morceau du message qu’ils étaient sûrs de trouver au sein du message codé, puis ils s’arrangeaient pour le placer en sachant que si deux lettres étaient identiques dans le message codé et dans le message clair, il fallait chercher ailleurs dans le message.
-
Il y avait en réalité 3 rotors à choisir parmi 5. Ce qui déjà permettait d’avoir possibilités de choix de rotors.
↩ -
Si on considère qu’une année fait 365.25 jours et qu’une journée comporte 86400 secondes, il faut plus de cinq mille milliards d’années pour toutes les tester au rythme d’une tentative par seconde !
↩
DES
En 1973, le NBS1, bureau américain de la normalisation a décidé qu’il fallait un standard dans le domaine de la cryptographie de données qui pourrait être utilisée dans les entreprises. Et il s’avère que Horst Feistel avait, deux ans plus tôt, inventé un algorithme qu’il avait baptisé Lucifer2. Ce dernier plaisait bien au NBS, mais quand la NSA s’en est mêlée, le NBS a été obligé d’accepter la modification apportée par l’agence de sécurité sur ce même algorithme. Cette modification n’était autre qu’une résistance supplémentaire à certaines attaques par cryptanalyse. Certains iraient même jusqu’à dire que la NSA avait déjà cassé Lucifer et qu’ils voulaient un algorithme plus complet pour chiffrer leurs documents, d’autres disent que la NSA voulait affaiblir Lucifer en créant DES pour pouvoir lire toutes les données, mais tout le monde sait que ce ne sont que calomnies et que la NSA ne veut que notre bien sur internet, non ? 
DES veut dire Data Encryption Standard. Nous ne pourrions pas vous expliquer le fonctionnement détaillé de cet algorithme car ça nécessiterait bien plus qu’un article et que ça n’a pas réellement sa place ici. Mais c’est globalement un chiffrage 100 % électronique qui fonctionne avec une subdivision du document à chiffrer en blocs de 64 bits3 pour leur appliquer une clé de 64 bits également. Et une de ses particularités est que le document initial a une certaine taille, et que le document final (donc chiffré) fait sensiblement la même taille que le fichier initial. Chaque bit est chiffré sans ajouter d’informations (contrairement aux méthodes de Cardan par exemple).
Cet algorithme a été jugé obsolète par le NBS en 2001 et a été remplacé par AES qui se base sur le même genre d’opérations. Il aura donc tenu 34 ans entre 1977 et 2001 en tant que standard. DES a connu des améliorations peu avant son obsolescence tels que le triple DES, G-DES ou DES-X.
-
Actuellement appelé NIST, National Institute of Stadards and Technology.
↩ -
Ce nom vient du fait que Feistel travaillait sur un système qu’il avait appelé Demonstration mais ce nom était trop long, il a donc du le tronquer. Demonstration est devenu Demon qui est lui-même devenu Lucifer.
↩ -
Pour les non-adeptes de l’informatique, le bit est l’unité fondamentale en électronique. Ça représente un chiffre dans un codage binaire. bit vient de la contraction de binary digit, ce qui veut dire chiffre binaire.
↩
RSA
L’algorithme RSA tient son nom de ses trois inventeurs (Rivest, Shamir et Adleman), respectivement Américain, Israélien et Américain. C’est un algorithme particulier car contrairement à DES, il est dit algorithme asymétrique. C’est-à-dire qu’il se base sur une clé publique pour chiffrer et d’une clé privée pour déchiffrer tel que la clé publique seule ne peut nous être utile car bien trop longue à analyser. Nous n’allons cependant pas vous expliquer son fonctionnement car il est également fort complexe pour avoir sa place dans un article et également parce que Vayel et Dominus Carnufex s’en sont déjà donné la peine. Vous pouvez trouver leur cours juste ici.
Vous devez tout de même savoir que cet algorithme est très efficace car utilisé entre autres dans les échanges bancaires et d’autres données qui nécessitent un haut degré de sécurité. La raison est simple : la clé publique est la multiplication de deux nombres premiers (de préférence très longs) tels que des ordinateurs sont incapables de la factoriser pour retrouver les multiples qui ont servi à chiffrer le document. Peut-être qu’un jour les ordinateurs seront capables de déterminer les facteurs premiers d’un nombre de 200 chiffres, mais ce n’est pas pour tout de suite. Et quand bien même ça arriverait, ils seront également capables de produire des nombres beaucoup plus gros. Le RSA est donc hautement sécurisé et jusqu’à présent considéré comme sans faille du moment que la clé publique est suffisamment longue.
La cryptographie quantique
N’ayez pas peur, il n’est pas nécessaire d’être un pro en mécanique quantique pour pouvoir comprendre ce qui suit. D’ailleurs, la mécanique quantique n’est pas aussi difficile qu’a essayé de vous faire croire votre prof de physique, vous allez voir. 
Il est important de savoir que ce que l’on appelle la cryptographie quantique n’est pas une nouvelle méthode de cryptographie mais uniquement un moyen de sécurité supplémentaire. Nous allons vous énoncer deux propriétés de la physique quantique qui sont importantes pour comprendre ce qui suit.
En mécanique quantique, il est question d’une particule un peu particulière : le quantum. Ce quantum est comme il vient de vous être dit une particule, donc bien plus petit qu’un atome. On parle alors de physique subatomique. Ces quantums répondent à plusieurs propriétés qui dictent leur comportement. Parmi ces propriétés, il y en a deux très importantes dans ce qui nous intéresse :
- le fait qu’un quantum peut se trouver dans un et un seul état à un instant donné, mais avec plusieurs valeurs simultanément (la superposition quantique) ;
- le fait que l’on ne peut mesurer les différentes valeurs sans détruire le quantum.
Ça peut paraître plutôt étrange car les lois de la physique quantique sont assez différentes de celles de la mécanique classique. Mais ne vous inquiétez pas, la première propriété nous dit que ces particules ont une certaine probabilité (qui est un nombre complexe) pour chaque valeur et que donc le quantum doit simuler toutes les valeurs d’un même état en même temps.
Pour les matheux :
Un état quantique se note avec la notation bra-ket tel que t.q. . Ce qui veut dire qu’un quantum dans un état est en réalité en une somme d’états quantiques de valeur de probabilité complexe . De plus, la somme des carrés des normes de ces probabilités complexes doit être égale à 1. Donc .
La seconde propriété dit que pour savoir quelle est la valeur précise du quantum, il nous faut le modifier et donc le faire disparaitre en tant qu’entité quantique. Pourquoi ? Car une fois la valeur mesurée, les coefficients (correspondant à la probabilité) de chaque valeur est changée en zéro, sauf une qui vaut un. Nous n’avons donc plus une entité quantique mais bien une entité ce qu’il y a de plus classique.
Pour les matheux :
Un quantum a beau être simultanément dans n états de probabilité chacun, on ne peut mesurer qu’un seul de ces . Et la probabilité que l’état soit mesuré plutôt qu’un autre est de . Une fois le quantum mesuré, sa valeur est figée à , les probabilités sont mises à 0 pour tout et est mise à 1.
Pourquoi ces notions nous sont-elles importantes ? Car il faut les assimiler pour comprendre l’ampleur de la cryptographie quantique. Habituellement, la cryptographie quantique est utilisée dans le domaine des chiffrages symétriques (donc avec une clé privée) afin de faire transiter cette même clé. Alors, il a été décidé de passer uniquement la clé par le canal quantique (qui n’est autre que le moyen de faire circuler le flux de quantum) et non directement le message en clair pour deux grandes raisons :
- La première est le fait qu’on peut savoir si le message a été intercepté et lu, mais on ne peut le faire disparaitre. Donc si le message en clair est intercepté, on est embêté. Il a donc fallu le chiffrer tout d’abord. Or, qui dit message chiffré (toujours en utilisant un algorithme symétrique) dit clé nécessaire pour le déchiffrer. Il faut donc communiquer la clé au destinataire. Et c’est là que notre canal quantique se révèle très intéressant. Si on voit que la clé a été interceptée, ce n’est pas grave, il suffit de la changer et d’en renvoyer une nouvelle.
- La seconde est le fait qu’il est impossible de transmettre de l’information sans perte ou sans modification (qu’on appelle bruit). Dans le domaine quantique, ce bruit reste assez élevé, et donc plus le message envoyé est long, plus il est risqué qu’il soit corrompu. C’est donc la clé (qui est relativement courte) qui doit être transférée pour limiter le bruit.
L’informatique classique travaille avec comme unité fondamentale le bit, et l’informatique quantique travaille avec une autre unité fondamentale qui en est inspirée : le qubit (également noté qbit). Mais un problème persiste : nous ne disposons pas de ces magnifiques quantums ou qubits. Il nous faut donc les simuler en utilisant un procédé tiers. Et c’est la polarisation de photons qui est la plus utilisée jusqu’à présent. Il faut donc obligatoirement un câble de fibre optique afin de servir de moyen de communication entre le destinateur et le destinataire. Un gros désavantage est que plus le câble est long, plus le bruit augmente. Il faut donc faire un compromis entre la longueur de l’information envoyée et la distance qu’elle peut parcourir. Actuellement, quelques dizaines de kilomètres restent une limite à la propagation d’information sous forme quantique.
PGP de Zimmerman
En 1991, Phil Zimmerman, un Américain décide que tout le monde a droit à une vie privée, même les pays étant soit sous dictature, soit analysés par les hautes instances de l’État. Ça lui a d’ailleurs valu beaucoup d’ennuis avec la justice américaine qui considérait la cryptographie comme un outil de guerre indisponible aux civils. Il a trouvé un système fonctionnant à moitié avec une clé privée et à l’autre moitié avec une clé publique. Ce n’est pas réellement un chiffrage asymétrique mais c’en est inspiré. PGP veut dire Pretty Good Privacy qui peut se traduire en vie relativement bien privée.
Cette méthode n’est pas une révolution et n’a pas apporté de grands changements dans le domaine de la cryptographie au sens purement analytique, mais il est important d’en parler car il y a 25 ans, beaucoup d’états interdisaient une privacy donc une vie privée à leur population. Et c’est partiellement à Phil Zimmerman que l’on doit ce droit qui nous a été donné.
C’est ainsi que s’achève ce dernier article sur l’histoire de la cryptographie. Nous espérons vraiment que vous y avez appris des choses ou au moins que ça vous a diverti. Si vous estimez un oubli une erreur quelque part, veuillez nous en faire part dans la section de commentaires prévue à cet effet.
Sources et liens
- Pour le cylindre de Jefferson, voici un article plus détaillé et la page Wikipédia qui est plus concise ;
- sur le PlayFair de Wheatstone, un petit exemple ;
- concernant le masque jetable de Vernam, un bonus ;
- sur Enigma, vidéo explicative (anglais), explication plus complète (anglais) ;
- à propos du DES : la page Wikipédia résume bien l’idée ;
- sur RSA : le cours de Vayel et Dominus Carnufex ;
- pour la cryptographie quantique, page assez complète de Wikipédia, document d’explication requérant la compréhension des notations quantiques (vecteurs quantiques et notation bra-ket) ;
- et enfin sur PGP, le site web de PGP, celui de Phil Zimmerman, la page Wikipédia (anglais car bien plus complète que la page française).












