Plus le temps passe, plus les ordinateurs semblent gagner en performances. Du moins, c'est la théorie. Dans les faits, les augmentations de performances sont devenues particulièrement faibles ces dernières années. Si vous regardez les benchmarks effectués par les divers sites de comparaison de matériel, vous verrez que les performances n'augmentent réellement qu'assez peu.
Pourtant, on entend souvent certains dire que la performance des ordinateurs augmente tous les 18 mois ou tous les deux ans : il s'agit d'une interprétation fréquente de la loi de Moore. Mais alors pourquoi cette augmentation de performance n'est-elle pas visible dans les benchmarks ? Pour le comprendre, il va falloir étudier plus en détail la loi de Moore, ainsi que d'autres lois affiliées.
Équation de la performance d'un processeur
Le temps que met un programme pour s’exécuter dépend :
- du temps mis par le processeur pour exécuter ses instructions ;
- du temps passé à attendre des données en provenance de cette feignasse de mémoire ;
- et du temps passé à attendre que ces *%¨"#|-[ de périphériques fassent ce qu'on leur demande !
Dans la réalité, vous pouvez être certains que votre programme passera les 3/4 de son temps à attendre la mémoire et les périphériques. La situation actuelle est telle qu'il est impossible de créer des programmes rapides sans prendre en compte la hiérarchie mémoire.
Dans cet article, on ne va s'intéresser qu'au processeur. Le temps pris par un programme pour exécuter ses instructions, qu'on notera $T$, dépend :
- du nombre moyen $N$ d'instructions exécutées par notre programme ;
- du nombre moyen de cycles d'horloge nécessaires pour exécuter une instruction, qu'on notera $CPI$ (ce qui est l'abréviation de Cycle Per Instruction) ;
- et de la durée $P$ d'un cycle d'horloge.
On peut récrire cette équation en remplacant la durée d'un cycle d'horloge par la fréquence (l'inverse de cete durée), ce qui donne la formule suivante.
Cette équation nous dit qu'augmenter la performance d'un processeur demande :
- soit de diminuer le nombre d'instructions d'un programme ;
- soit de diminuer le nombre de cycles par instruction ;
- soit d'augmenter la fréquence.
Augmenter la fréquence
Pour augmenter la fréquence, il faut utiliser des composants électroniques plus rapides. Presque tous les composants d'un ordinateur sont fabriqués avec un grand nombre de transistors. Un transistor est simplement un composant relié à un circuit électronique par trois morceaux de "fil" conducteur que l'on appelle broches : la grille, le drain et la source. Dans les processeurs, on utilise notre transistor comme un interrupteur qui réagit en fonction de sa grille : suivant la tension appliquée sur la grille, le transistor conduira ou ne conduira pas le courant entre la source et le drain.

Miniaturisation et fréquence
Diminuer la taille des transistors permet de les rendre plus rapides. C'est un scientifique du nom de Robert Dennard qui a découvert un moyen de rendre un transistor plus rapide en diminuant certains de ses paramètres physiques. De plus, la vitesse de transmission des bits dans les fils d'interconnexions est proportionnelle à leur longueur : plus ces fils seront courts, plus la transmission sera rapide. Ce qui est clairement un second effet positif de la miniaturisation sur la fréquence.
Et il se trouve qu'il existe des lois concernant l'évolution de la miniaturisation des transistors dans le temps. En 1965, le cofondateur de la société Intel, spécialisée dans la conception de mémoires et de processeurs, a affirmé que la quantité de transistors présents dans un processeur doublait tous les 18 mois. Cette affirmation porte aujourd'hui le nom de première loi de Moore. En 1975, le cofondateur d'Intel réévalua cette affirmation : ce n'est pas tous les 18 mois que le nombre de transistors d'un processeur double, mais tous les 24 mois. Cette nouvelle version, appelée la seconde loi de Moore, a redoutablement bien survécu : elle est toujours valable de nos jours.
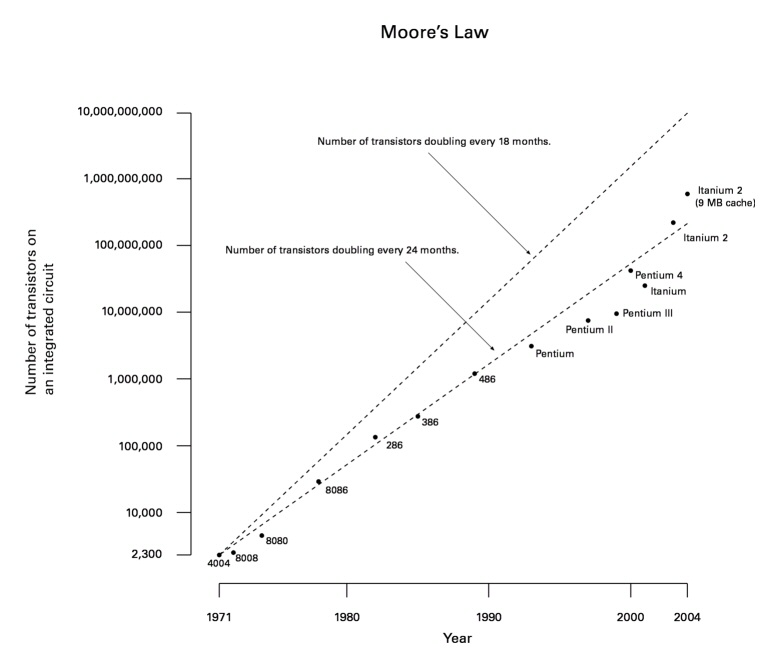
On pourrait croire que doubler le nombre de transistors signifie diviser par deux les dimensions d'un transistor et donc doubler la fréquence. En réalité, les transistors et les fils sont réunis sur une surface : qui dit diminution par deux de la surface signifie division par $\sqrt{2}$ des cotés de cette surface. Ainsi, les dimensions des transistors et des fils sont divisés par $\sqrt{2}$. Ce faisant, la fréquence des processeurs est multipliée par $\sqrt{2}$ tous les deux ans, ce qui donne environ 40% de performances en plus tous les deux ans.
Du moins, c'est la théorie… En réalité, cette augmentation de 40% n'est qu'une approximation : la fréquence effective d'un processeur dépend fortement de sa conception (de la longueur du pipeline, notamment) et des limites imposées par la consommation thermique.
Miniaturisation et efficacité énergétique
Avec le temps, il est devenu de plus en plus difficile de monter en fréquence. En effet, augmenter la fréquence a tendance à faire chauffer le processeur : on observe donc une augmentation de la consommation énergétique des processeurs au fil du temps. Et aussi bizarre que cela puisse paraitre, l'efficacité énergétique de nos processeurs n'a pas cessé d'augmenter : pour le même travail, les processeurs chauffent moins. Plus précisément, l'efficacité énergétique double tous les 1,57 ans : c'est la loi de Kommey.
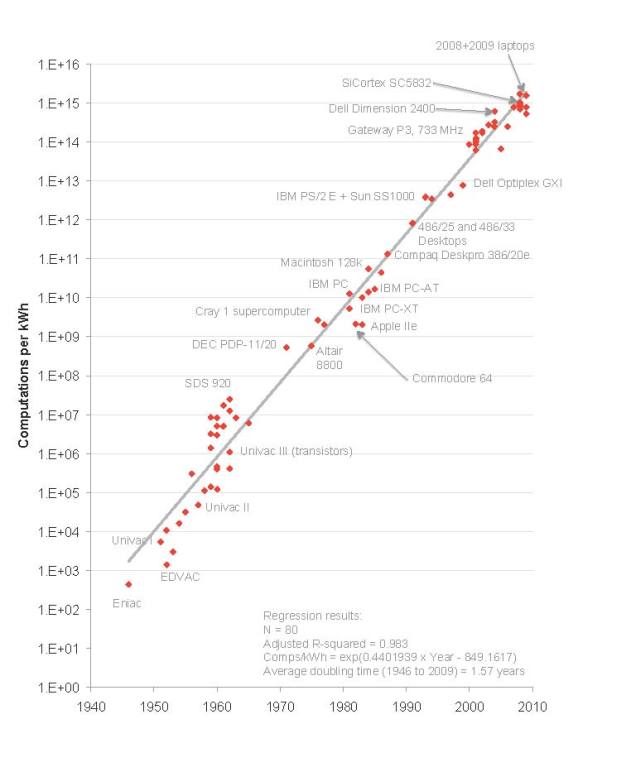
Augmenter le CPI
Les hausses de performances peuvent aussi provenir de la micro-architecture des processeurs. L'ajout d'unités de calcul, de meilleures unités de prédiction de branchements, et autres ajouts de circuits sont une source importante d'augmentation de performance. Toutes ces optimisations diminuent le $CPI$, à savoir le nombre de cycle d'horloge par instruction. Elles procédent de deux manières :
- diminuer le temps mis pour effectuer une instruction ;
- augmenter le nombre d'instructions exécutées en même temps.
Un seul coeur : la loi de Pollack
La seconde solution consiste à exécuter plusieurs instructions à la fois, à augmenter le débit d’instructions. Or, la loi de Pollack dit que cette augmentation de performances est approximativement proportionnelle à la racine carrée du nombre de transistors ajoutés : si on double le nombre de transistors, la performance est multipliée par $\sqrt{2}$. En utilisant la loi de Moore, on en déduit qu'on gagne approximativement 40% de performances tous les deux ans. En ajoutant ces gains aux gains provenant de l'augmentation en fréquence, on gagne tout au plus 80% de performances en plus tous les deux ans (deux fois 40%).
On peut expliquer cette loi de Pollack assez simplement. Il faut se rappeler que les processeurs modernes peuvent changer l'ordre des instructions pour gagner en performances (on parle d'éxecution dans le désordre). Pour cela, les instructions sont pré-chargées dans une mémoire tampon, de taille fixe. Cependant, le processeur doit gérer les situations où une instruction a besoin du résultat d'une autre pour s'exécuter : chaque instruction doit être comparée à toutes les autres, pour savoir quelle instruction a besoin des résultats d'une autre. Avec $N$ instructions, vu que chacune d'entre elles doit être comparée à toutes les autres, ce qui demande $N^2$ comparaisons. En doublant le nombre de transistors, on peut donc doubler le nombre de comparateurs, ce qui signifie que l'on peut multiplier le nombre $N$ d'instructions par $\sqrt{2}$.
Même chose pour les processeurs superscalaires, qui peuvent démarrer $N$ instructions simultanément : l'analyse mathématique nous dit que le nombre de transistors nécessaire pour exécuter simultanément $N$ instructions avec une mémoire tampon capable de mémoriser $M$ instructions demande $N^2 \times M^2$ portes logiques/transistors. On retrouve donc la loi de Pollack : multiplier par $X$ le nombre de transistors permet juste d’exécuter $\sqrt{X}$ instructions simultanées en plus et de garder $\sqrt{X}$ instructions en attente en plus.
Multicœurs : contourner la loi de Pollack
On peut cependant contourner la loi de Pollack, qui ne vaut que pour des processeurs mono-cœur. Mais en utilisant plusieurs cœurs, la performance est la somme des performances individuelles de chaque cœur. Ainsi, doubler le nombre de transistors permet de doubler le nombre de cœurs et donc de doubler la performance. Ce qui est mieux qu'une amélioration de 40%. On voit donc qu'augmenter le nombre de cœurs est plus rentable que d'augmenter le débit de chaque cœur : cela permet de contourner la loi de Pollack. On comprend pourquoi les constructeurs n'ont de cesse d'augmenter le nombre de cœurs de nos processeurs…
Toutes ces augmentations de performances, c'est bien beau, mais il existe une loi qui vient jouer les troubles-fêtes. La loi de Wirth nous dit que le logiciel ralentit toujours plus vite que le matériel. Évidemment, cette loi est assez approximative, et le créateur de cette loi (qui a aussi créé le langage Pascal) ne tire pas cette loi d'expériences ou de statiques (contrairement à toutes les autres lois). Mais avouez qu'elle a une part de vérité !






