Interpolation 1D avec Matlab

Comprendre interp1 et savoir choisir ses options

Si vous souhaitez, notamment,

  • rééchantillonner des signaux,
  • estimer une fonction coûteuse en un point à partir des valeurs en d’autres points,
  • tracer des courbes lissées à partir d’un faible nombre de points,

alors vous aller avoir besoin d’interpoler, voire d’extrapoler !

La fonction interp1 de Matlab permet d’effectuer des interpolations et extrapolations à une dimension. Nous verrons dans ce tutoriel comment l’utiliser, et surtout comment choisir ses paramètres en fonction de vos besoins.

Syntaxe

Nous nous concentrerons sur l’usage avec tous les arguments, y compris optionnels.1 Cet usage se résume par la ligne suivante :

1
vq = interp1(x, v, xq, method, extrapolation);

où :

  • x est le vecteur des abscisses des points d’échantillonnage,
  • v est le vecteur des valeurs d’échantillonnage, correspondant à x.
  • xq est le vecteur des abscisses des points dont on souhaite interpoler la valeur,
  • method est la méthode d’interpolation (à choisir notamment entre 'nearest', 'linear', 'pchip' et 'spline'),
  • extrapolation est la stratégie d’extrapolation (soit 'extrap', soit une constante numérique),
  • vq est le vecteur des valeurs interpolées.

Autrement dit, vq = interp1(x, v, xq, method, extrapolation) retourne la valeur vq aux points xq de la fonction valant v aux points x, et dont la valeur en dehors de ces points est calculée en utilisant la méthode d’interpolation method et la stratégie d’extrapolation extrapolation.

  1. Pour les formes raccourcies, voir la documentation officielle. ↩

Exemple travaillé

Pour clarifier les explications de la section précédente, nous allons travailler sur un exemple.

Imaginons que l’on dispose de relevés de l’élévation du soleil dans le ciel toutes les heures entre 9 heures et 19 heures.

1
2
temps =[9 10 11 12 13 14 15 16 17 18 19];
elevation =[28.5 40 50 60 67.5 70 65 56 45.5 35 23];

On souhaite estimer la position du soleil de 8 heures à 20 heures avec une résolution d’un quart d’heure, de sorte que le vecteur de temps que l’on souhaite est le suivant.

1
tempsInterp = 8:0.25:20;

Pour estimer l’élévation pour chaque valeur du vecteur précédent, il est nécessaire d’interpoler et d’extrapoler car les données ont seulement une résolution d’une heure et que les relevés n’ont été effectués que de 9 heures à 19 heures.

Pour guider notre choix de méthode d’interpolation et une stratégie d’extrapolation, on examine les informations dont on dispose sur la courbe. On sait que la fonction qui représente l’élévation en fonction du temps est:

  • continue (le soleil ne saute pas de position),
  • à dérivée continue (la vitesse d’élévation ne change pas brutalement),
  • à dérivée seconde continue (si la vitesse d’élévation varie, alors elle varie continûment).

Les informations ci-dessous signifient que la fonction est au moins de classe $C^2$. La méthode d’interpolation 'spline' et la méthode d’extrapolation 'extrap' semblent des choix judicieux (voir la partie suivante pour plus de détails sur le choix d’une méthode d’interpolation).

1
elevationInterp = interp1(temps, elevation, tempsInterp, 'spline', 'extrap');

Visualisons le résultat obtenu !

1
2
3
4
5
6
7
8
9
figure;
scatter(temps, elevation, 'o');
hold all;
scatter(tempsInterp, elevationInterp, 'x');
xlabel('Temps (heures)');
ylabel('Élévation (°)');
title('Élévation du soleil au cours d''une journée');
legend('mesures','interpolation');
ylim([0 80]);
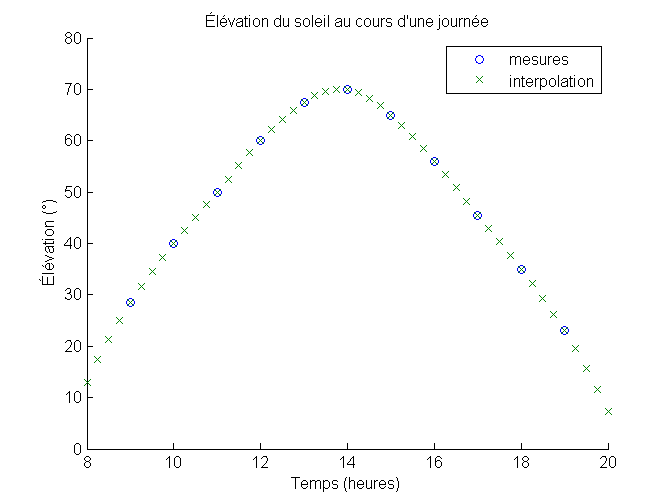
Mesures et résultat de l’interpolation.

Choisir les options adéquates

Choisir les bonnes méthodes d’interpolation et d’extrapolation n’est pas trivial dans la plupart des cas. Cette section vise à vous guider pour choisir en connaissance de cause.

Méthode d’interpolation

nearest

Si vous souhaitez une très grande performance au détriment de la continuité, alors 'nearest' est fait pour vous ! Vous aurez la plus grande rapidité possible, mais la précision peut en pâtir, puisque la fonction d’interpolation n’est pas continue. Vous aurez des marches d’escalier. Elle nécessite au minimum deux points.

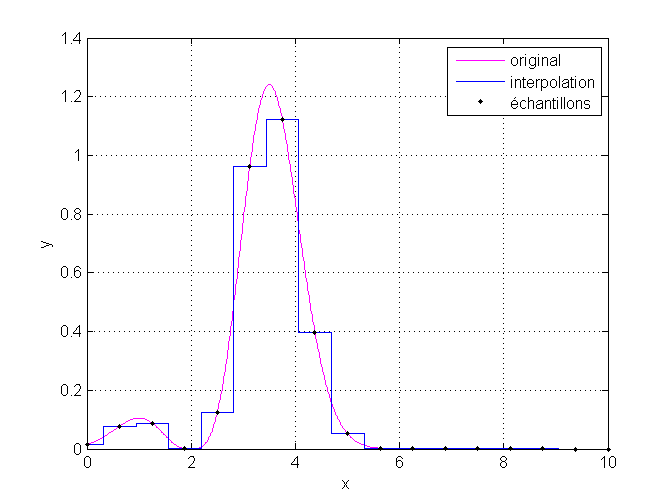
Interpolation au plus proche. Le résultat est peu fidèle, mais la fonction est performante.

Vous retrouverez ci-dessous le script ayant généré le graphique ci-dessus.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
f = @(x) abs(exp(-(x-2.5).^2).*(x-2).^3);
nSamples = 17;
xSamples = linspace(0, 10, nSamples);
ySamples = f(xSamples);
xInterp = linspace(-1, 11, 10000);
yNearest = interp1(xSamples, ySamples, xInterp, 'nearest', NaN);

figure;
plot(xInterp, f(xInterp), '-m');
hold all;
stairs(xInterp, yNearest, 'b');
scatter(xSamples, ySamples, '.k');
xlim([0 10]);
grid on;
legend('original', 'interpolation','échantillons');
xlabel('x');
ylabel('y');

linear

La méthode 'linear' fournit une fonction d’interpolation continue. C’est un bon compromis entre performance et précision. Elle fournit une fonction linéaire par morceau, avec des cassures aux points de données. C’est la méthode à choisir si vous n’avez pas de contrainte particulière de continuité ou de performance. Elle nécessite au minimum deux points.

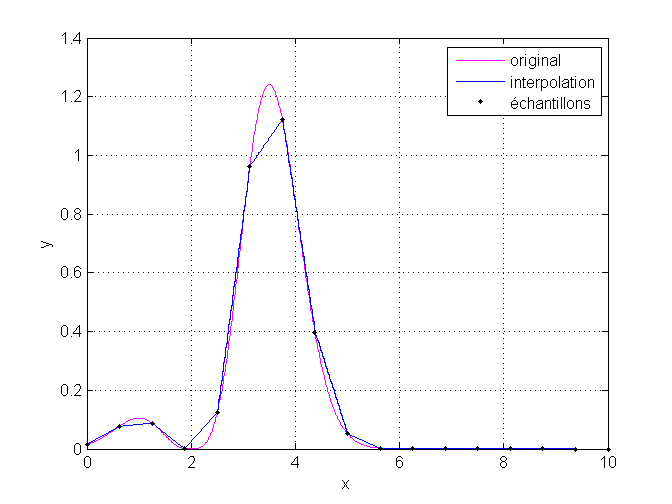
Interpolation linéaire. On voit bien les cassures. Comme les points sont très espacés, les pics ont tendance à être coupés.

Vous retrouverez ci-dessous le script ayant généré le graphique ci-dessus.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
f = @(x) abs(exp(-(x-2.5).^2).*(x-2).^3);
nSamples = 17;
xSamples = linspace(0, 10, nSamples);
ySamples = f(xSamples);
xInterp = linspace(-1, 11, 10000);
yNearest = interp1(xSamples, ySamples, xInterp, 'linear', NaN);

figure;
plot(xInterp, f(xInterp), '-m');
hold all;
stairs(xInterp, yNearest, 'b');
scatter(xSamples, ySamples, '.k');
xlim([0 10]);
grid on;
legend('original', 'interpolation','échantillons');
xlabel('x');
ylabel('y');

pchip

Pour avoir une fonction d’interpolation à dérivée continue, il faut passer à la méthode 'pchip', qui se base sur des splines cubiques de Hermite. Cette méthode présente l’avantage de préserver la forme : sur chaque intervalle, la fonction d’interpolation est monotone, et donc ne dépasse pas les points de données. Par contre, les crêtes peuvent être coupées. Elle nécessite au minimum quatre points.

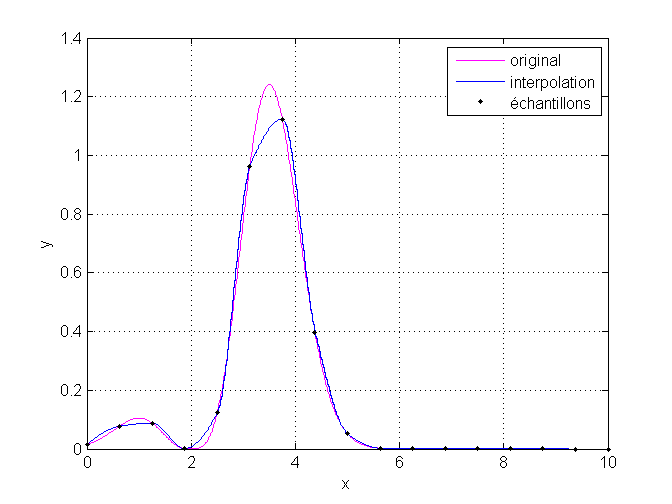
Interpolation 'pchip'. L’interpolation est lisse, il n’y a pas de dépassements des points de données.
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
f = @(x) abs(exp(-(x-2.5).^2).*(x-2).^3);
nSamples = 17;
xSamples = linspace(0, 10, nSamples);
ySamples = f(xSamples);
xInterp = linspace(-1, 11, 10000);
yNearest = interp1(xSamples, ySamples, xInterp, 'pchip', NaN);

figure;
plot(xInterp, f(xInterp), '-m');
hold all;
stairs(xInterp, yNearest, 'b');
scatter(xSamples, ySamples, '.k');
xlim([0 10]);
grid on;
legend('original', 'interpolation','échantillons');
xlabel('x');
ylabel('y');

spline

La méthode 'spline' est la plus lisse fournie par Matlab. Il s’agit d’un interpolateur à dérivée seconde continue. La fonction d’interpolation est ainsi très lisse, et permet de représenter assez bien les pics. Elle a malheureusement tendance à créer des ondulations1 si les données forment des plateaux. Elle nécessite au minimum quatre points.

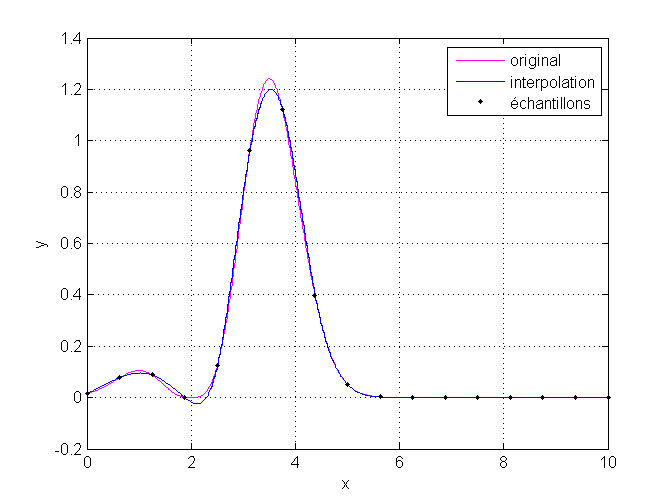
Interpolation spline. La courbe est lisse, le pic est moins atténué, mais on observe des ondulations qui n’apparaissent pas avec 'pchip'.

Vous retrouverez ci-dessous le script ayant généré le graphique ci-dessus.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
f = @(x) abs(exp(-(x-2.5).^2).*(x-2).^3);
nSamples = 17;
xSamples = linspace(0, 10, nSamples);
ySamples = f(xSamples);
xInterp = linspace(-1, 11, 10000);
yNearest = interp1(xSamples, ySamples, xInterp, 'spline', NaN);

figure;
plot(xInterp, f(xInterp), '-m');
hold all;
stairs(xInterp, yNearest, 'b');
scatter(xSamples, ySamples, '.k');
xlim([0 10]);
grid on;
legend('original', 'interpolation','échantillons');
xlabel('x');
ylabel('y');

Synthèse

Le tableau ci-dessous résume les caractéristiques des différentes méthodes d’interpolation.

Méthode Rapidité Empreinte mémoire Localité Continuité Nombre minimum de points
nearest très grande faible grande NA 2
linear grande moyenne grande C0 2
pchip moyenne grande moyenne C1 4
spline faible très grande faible C2 4

Autres méthodes

Matlab propose d’autres méthodes d’interpolation, je vous laisse regarder en détail la documentation.

Extrapolation

L’extrapolation est un sujet délicat. Dans la majorité des cas, je conseille d’éviter les extrapolation. Si vous êtes forcé à le faire, interp1 propose deux méthodes.

A partir de la méthode d’interpolation ('extrap')

La première consiste à extrapoler en se basant sur la méthode d’interpolation. Pour cela, il faut utiliser le paramètre 'extrap'.

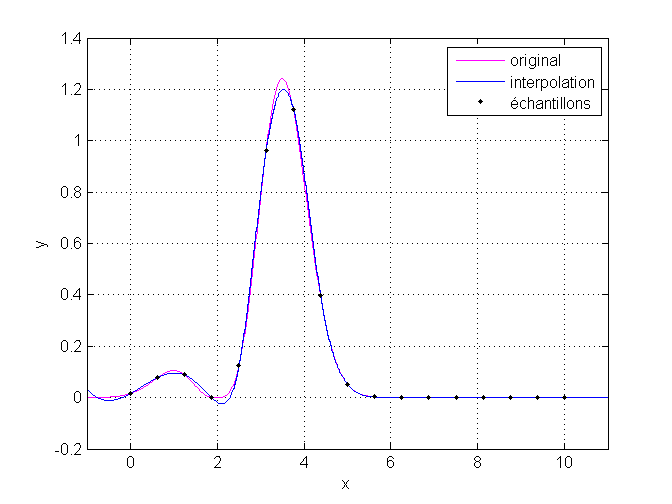
Extrapolation 'extrap'.

Vous retrouverez ci-dessous le script ayant généré le graphique ci-dessus.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
f = @(x) abs(exp(-(x-2.5).^2).*(x-2).^3);
nSamples = 17;
xSamples = linspace(0, 10, nSamples);
ySamples = f(xSamples);
xInterp = linspace(-1, 11, 10000);
yNearest = interp1(xSamples, ySamples, xInterp, 'spline', 'extrap');

figure;
plot(xInterp, f(xInterp), '-m');
hold all;
stairs(xInterp, yNearest, 'b');
scatter(xSamples, ySamples, '.k');
xlim([-1 11]);
grid on;
legend('original', 'interpolation','échantillons');
xlabel('x');
ylabel('y');

Avec une valeur numérique constante

Autrement, il est possible de spécifier une valeur qui sera utilisée pour tous les points tombant en dehors de l’étendue des $x_i$.

Extrapolation à valeur constante.

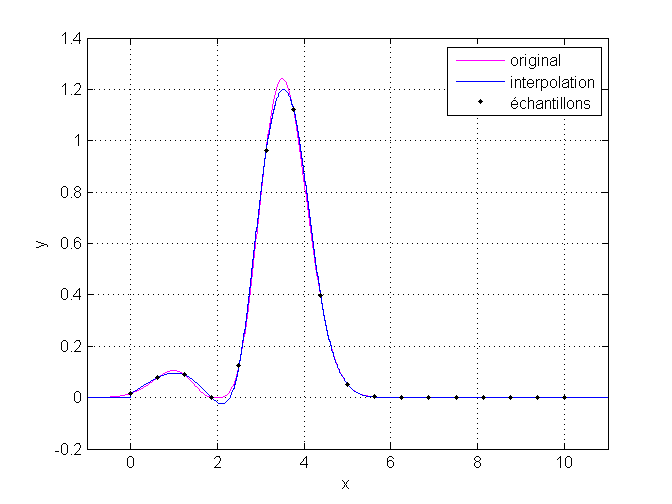
Vous retrouverez ci-dessous le script ayant généré le graphique ci-dessus.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
f = @(x) abs(exp(-(x-2.5).^2).*(x-2).^3);
nSamples = 17;
xSamples = linspace(0, 10, nSamples);
ySamples = f(xSamples);
xInterp = linspace(-1, 11, 10000);
yNearest = interp1(xSamples, ySamples, xInterp, 'spline', 0);

figure;
plot(xInterp, f(xInterp), '-m');
hold all;
stairs(xInterp, yNearest, 'b');
scatter(xSamples, ySamples, '.k');
xlim([-1 11]);
grid on;
legend('original', 'interpolation','échantillons');
xlabel('x');
ylabel('y');

Cette utilisation correspond parfois à un cas où l’on ne contrôle pas parfaitement les données d’entrées (paramètres de l’utilisateur, sortie d’un autre script, etc). Il est dans ce cas intéressant de marquer ces valeurs grâce à la valeur spéciale NaN.

  1. Il s’agit d’un phénomène similaire au phénomène de Gibbs et au phénomène de Runge. ↩

Vous savez désormais comment interpoler à une dimension avec Matlab, ainsi que choisir au mieux les paramètres en fonction de votre problème et de vos données.

Si êtes curieux et souhaitez en apprendre plus, les quelques liens suivant devraient élargir vos horizons.

Références

Sur le fonctionnement de Matlab

Sur l’interpolation au plus proche

Sur l’interpolation linéaire

Sur l’interpolation cubique de type pchip

Sur l’interpolation cubique de type spline

Aucun commentaire

Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte