- Un problème mathématique pour se distraire au volant
- Petite leçon de Vim : Apprendre à gérer ses motions
Je viens partager, avec toi, un droit de réponse/rectification que je m’étais octroyé il y a un an environ. Après avoir écrit, j’ai laissé reposer, puis ai fini par oublier ma cape de redressement de tort.

Mais comme il y a des pépins intéressants dans le fruit, je te le livre après remodelage. Au menu, on s’initiera à la NPI et on va parcourir l’histoire des calculateurs de poche… de marque HP et autres, sauf NASA.
Salut Dominique,
J’ai lu avec un certain intérêt ton billet du 25/juin/2020 sur la HP-21. Les commentaires n’étant pas activés dessus, j’ai préféré donc t’écrire.
Je ne prétendrai pas posséder la vérité et mon avis n’est même pas celui de propriétaire ou ex usager de ce modèle. C’est juste le partage de ma réflexion et de mes observations de passionné d’histoire du calcul, probablement un peu couplées à mon ressenti d’usager de la marque.
vive les HP
« Team premier degré » Je vais rappeler les faits qui, selon moi, expliquent l’aura des calculatrices de la marque et pourquoi elles fascinent.
1ère complète de bureau
D’abord, un petit retour en/aux arrière/origines, avec d’abord le modèle 9100A prototypé dès 1964 et mis sur le marché en 1968 : c’est la première « calculatrice de bureau » programmable et à la fois scientifique (contrairement à la concurrence) et financière.

Cette machine était typiquement un micro-ordinateur (PC) au même titre que le Olivetti Programma 101 de 1965 (dont Hewlett-Packard a copié quelques principes conceptuels) et le Micral N de 1973, mais a été présenté comme une calculatrice professionnelle (ou de bureau), appellation qu’on doit aussi à cette marque, comme l’explique Bill Hewlett :
Si nous avions appelé cela un ordinateur, il aurait été rejeté par les gourous de l’informatique de nos clients, car il ne ressemble pas à un IBM. Nous avons ainsi décidé d’appeler cela une calculatrice et toutes ces absurdités ont disparu
1ère scientifique de poche
Le second coup d’éclat de la marque sera avec le modèle 35 mis sur le marché en 1972 : c’est la première « calculatrice de poche » scientifique (contrairement au prototype Texas Instruments Cal Tech de 1967 puis les japonais dès 1970 : Sanyo ICC-0081 "Mini Calculator", Canon Pocketronic, Sharp QT-8B "micro Compet") Ce modèle utilise un affichage DEL et fonctionne sur pile (comme les concurrents sortis en 1971 : Sharp EL-8, Mostek MK6010, Busicom LE-120A "HANDY", Digitron DB 800, Bowmar 901B ; et ceux de 1972 et 1973 : Sinclair Executive, Elektronika B3–04, Sinclair Cambridge.) Mais outre le fait de tenir en poche (comme d’autres d’acteurs de plus en plus nombreux), elle va reléguer au placard les règles à calculer et les bonnes vieilles tables logarithmiques/trigonométriques/etc.

Bien entendu, on entend par « calculatrice scientifique » toute calculatrice
électronique possédant diverses possibilités d’applications scientifiques : fonctions trigonométriques usuelles, calcul de logarithmes ou, dans le cas des calculatrices graphiques, la capacité de tracer des graphiques.

catégorie | fonctions |
|---|---|
Trigonométrie | sin (sinus), arc sin (arc sinus), cos (cosinus), arc cos (arc cosinus), tan (tangente), arc tan (art tangente) |
Logarithmique | log (logarithme décimal), ln (logarithme népérien), ₑˣ (exponentiel) |
Exponentiation | ¹/ₓ (inverse), √𝑥 (racine carrée), yˣ (puissance quelconque) |
Constante, Autre | π (Pi), CH S (±), E EX (exposant de notation scientifique) |
Registre Mémoire | sto (store), rcl (recall), clr (clear all register), cl𝑥 (clear entry) |
éternel roc solide
L’aura de la marque, dans le secteur des calculatrices, vient d’abord du fait qu’elle est pionnière du calcul « scientifique » (là où les autres calculatrices étaient limitées aux quatre opérations seulement) ; ensuite de la qualité de construction (d’où découle la longévité et la solidité) ; enfin la grande précision de calcul (inégalée par les autres calculatrices) et autres détails (dont les touches biseautées.) Pour la petite histoire, la précision de cette calculatrice dépassait celle de la plupart des mainframes (gros ordinateurs centraux) de l’époque, notamment le Burroughs B5500 que la firme utilisait. Des employés de Texas Instruments ne s’y sont pas trompé en préférant utiliser les calculatrices de la concurrence.
De même, la solidité était dans le cahier des charges : Bill voulait que les calculatrices de poche puissent tomber de trois pieds (soit 0,9144 mètres) sans s’endommager (d’où aussi l’aspect un peu brut et mal fini du point de vue actuel), et Dave s’en est assuré empiriquement à la sortie.

Il faut ajouter à tout cela que la marque est connue pour son intégrité : malgré les vérifications minutieuses, de petits bogues (comme « 2 . 0 2 ln ₑˣ » –i.e. — qui indiquait 2 au lieu de 2.02) ont été découverts après que vingt-cinq milles unités de HP-35 aient été vendues ; ils en ont fait l’annonce publique et échangé les unités défectueuses par des unités corrigées de la nouvelle production. Assurément, l’aura de la marque est justifiée.
1ère financière de poche
Le troisième coup d’éclat de la marque fut de sortir, l’année suivante (1973), la première calculatrice de poche « financière » cette fois ci. Là aussi, elle est pionnière, et il faudra quelques temps avant que des produits concurrents arrivent (il faut par exemple attendre 1976 pour voir naître la gamme Texas Instruments Business Analyst, et bien des décades plus tard pour voir arriver Casio FC-200V et Sharp EL 738 entre autres.) On retrouve bien entendu la même qualité de fabrication et de la précision dans les calculs. Au lieu de fonctions scientifiques, on retrouve plutôt des accès directs aux calculs de pourcentages et TVM (pour les intérêts simples ou composés, et assimilés, plus amortissements et valeur actuelle.) On a aussi, pour la première fois, les statistiques (sommes, moyenne, variance) à une variable.

1ère programmable de poche
Vers fin 1974, la marque réussi le tour de force de faire rentrer sa 9100B en poche avec la sortie du modèle 65 : c’est véritablement la toute première calculatrice de poche « programmable » avec un lecteur de cartes magnétiques pour sauvegarder et charger des programmes. Cerise sur le gâteau, il y a, pour la première fois, la conversion de bases et les fonctions de calcul sur les degrés/minutes/secondes. Ce sera la première calculatrice dans l’espace, mettant les règles Aristo à la retraite :
Twenty-four minutes before the rendezvous in space, when the Apollo and Soyuz were 12 miles apart, the American astronauts corrected their course to place their spacecraft into the same orbit as the Russian craft. Twelve minutes later, they made a second positioning maneuver just prior to braking, and coasted in to linkup. In both cases, the Apollo astronauts made the course-correction calculations on their HP-65. Had the on-board computer failed, the spacecraft not being in communication with ground stations at the time, the HP-65 would have been the only way to make all the critical calculations. Using complex programs of nearly 1000 steps written by NASA scientists and pre-recorded on magnetic program cards, the astronauts made the calculations automatically, quickly, and with ten-digit accuracy. The HP-65 also served as a backup for Apollo’s on-board computer for two earlier maneuvers. Its answers provided a confidence-boosting double-check on the coelliptic (85 mile) maneuver, and the terminal phase initiation (22 mile) maneuver, which placed Apollo on an intercept trajectory with the Russian craft. Periodically throughout their joint mission, the Apollo astronauts also used the HP-65 to calculate how to point a high-gain antenna precisely at an orbiting satellite to assure the best possible ground communications.

L’impact de cette machine se retrouve aussi dans la naissance, en 1974, du fanzine 65-Notes. Le principe sera copié en 1976 en face et ce sera le 52-Notes, à côté du DDJ. Le fait est à souligner pour la simple raison qu’avant cela, il n’existait pas de publication papier, largement distribué (et de surcroit vers un public large) avec des listings de code…
1er leader en innovations
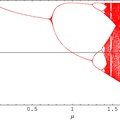
Si l’on compare à aujourd’hui, la HP-35 et son successeur HP-21 peuvent paraître bien banales car depuis lors la concurrence a eu le temps de se rattraper et la plupart de ces fonctionnalités sont sur les calculatrices d’entrée de gamme… Mais en remettant dans le contexte, ces machines sont fortement appréciées des scientifiques et ingénieurs qui avaient besoin de précision et d’exactitude comme sur un ordinateur… Par exemple, la découverte des premiers nombres de Feigenbaum ont été fait fait sur une HP-65 !
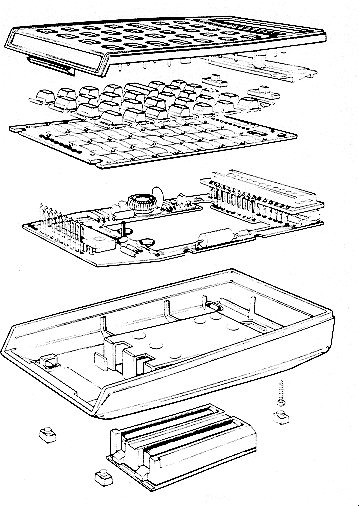
touches
Les premiers modèles de bureau, les 9100, ont apparemment repris les touches habituelles des claviers d’ordinateurs, mais ont bénéficié d’un certain soin notable.
The keyboard used the double shot injection molding process that helped make HP’s later handhelds legendary. (The characters on the keys are molded through and can’t wear off.) The key switches were specially designed to produce pleasing feel and proper feedback and had gold alloy contacts. The contacts were arranged in a matrix with an interlock to prevent errors due to multiple keys pressed simultaneously. Keys were debounced by delaying the key signal.
La seconde série de modèles de bureau, les 9800, se sont améliorés en utilisant une technologie dite sans friction et qui n’était réservé qu’aux machines haut de gamme.
The keyboards had a printed circuit board transformer under each key. Each key had a metal disk and when this disk was moved closer to the coils printed on the circuit board, it changed the transformer’s performance. This change was amplified by a comparator. This kind of keyboard was very reliable due to the lack of mechanical contacts.
La première génération de poche, dites Classics, et la seconde génération nommée Woodstock, a accordé un soin particulier aux touches.
HP took pride in using the latest industrial engineering research and their own ideas and studies. The spacing of the keys on the HP-35 was based on a simple test - they needed to work well with Dave Packard’s large fingers. Dick Osgood also analyzed how people pressed calculator keys. Based on the way that most people poked at the keys he designed a hinged key and avoided the "oil can feel" of TI and other calculators. It took many design iterations to get the final design which used bent beryllium copper strips. The key bottoms were designed to be easy on the copper while still providing the right feel. The keys were made with a state-of-the-art double shot injection molding technique. This was very difficult but ensured that key legends would never wear off. Since the keypads were subject to very little wear, they were printed until the HP-65. On the HP-65, the top legends had a magnetic card sliding over them and the metal oxide was abrasive, so these were also molded using a secret process. A difference between the key molding and the keypad molding is that there could be no enclosed spaces in the letters, so the R in the R↓ legend was not completely closed and other letters with closed spaces were avoided.
Dans le cas du HP-21, on pouvait lire dans l’article « Inside the New Pocket Calculators » d’un numéro de HP Journal de novembre 1975 :
Electrical integrity is provided by a flow-soldering operation which connects all electronic components to the logic board. All keys except the blue prefix key are molded in two clusters, which are mechanically separated during loading into the keyboard bezel. This reduces the number of parts handled from thirty to three and minimizes assembly operator errors and fatigue. That this innovation works is largely because of the creative efforts of the plastic mold designers and craftsmen of the HP Manufacturing Division, whose continuing high standards of excellence contributed much to the success of the HP-21. The over-center breakaway tactile feel of our former calculator keys has been retained, and the molded design of the key- strip actuating surfaces on the undersides of the keys eliminates the control bumps needed on earlier models.
Ce qu’il faut retenir, si bien résumé par un autre article de presse de l’époque : « Each key has a “breakaway” or “overcenter” touch similar to the key action of a high quality electric typewriter. » Ces touches, qui peuvent ne pas vous plaire aujourd’hui, ont été très appréciées sur les chantiers et dans diverses conditions où on a besoin d’être sûr de sa frappe sans constamment regarder l’écran (y compris avec des gants de chantier par exemple.)
prix
Pour les prix, Hewlett-Packard a pourtant proposé des modèles pour moult bourses, sans se brader en qualité, et ses calculatrices sont comparativement bien moins chères que celles de Texas Instruments encore aujourd’hui —lire par exemple les écrits glanés sur : reddit.com, mentalfloss.com, washingtonpost.com, thehustle.co, hpmuseum.org, etc—. Et les modèles de 1975 allaient dans ce sens : remplacer des modèles vieillissants (quoique pas vraiment en terme de fonctionnalité) par d’autres qui sont un peu plus compacts et bien moins chers avec un peu plus de fonctionnalités au passage. Mais le marché de l’antiquité et de l’occasion par contre sont sans réelle logique (l’offre et la demande n’expliquent pas tout, encore moins quand il y a des enchères…)
| old (year) | new (Woodstock) | extras |
|---|---|---|
| 35 (1972) | 21 (Pumpkin) | bascule degrés/radians, conversions polaire et rectangulaire, touche formatage d’affichage |
| 80 (1973) / 70 | 22 (Turnip) | 10 registres utilisateurs, TVM et bascule pour indiquer paiements en début/fin de période, 2 fonction logarithmiques, 2 calculs statistiques |
| 65 (1974) / 67 | 25 (Squash) | 8 registres, plus de lecteur de carte magnétique, programmable jusque 49 pas, notation ingénieur, plus de fonctions |
Les évolutions ne concernent pas que les calculatrices de poche ; celles de bureau aussi on droit à leur révolution…
Ainsi, la HP-45 va être déclinée en deux variantes avec un peu moins de fonctions (mais bien plus que la HP-35 et les mêmes innovations apportées alors) :
- HP-21 déjà évoquée comme modèle de poche moins cher.
- HP-46 comme modèle de bureau avec une imprimante par défaut (l’afficheur est un module optionnel), ouvrant la voie des calculatrices comptables (à ne pas confondre avec les caisses enregistreuses plus chères.)

- La 46 laissera la place à la HP-91, fonctionnant entièrement sur piles, en 1977.
De la même façon, la HP-80 va être déclinée aussi en deux variantes :
- HP-70 comme modèle de poche moins cher (et sans touche « shift ») en 1974.
- La 70 laissera la place à la HP-22 (plus de fonctionnalités pour un prix équivalent) en 1975.
- HP-81 comme modèle de bureau avec une imprimante par défaut (l’afficheur est un module optionnel), avec plus de registres et de modes et l’extension de certaines fonctions.
- La 81 laissera la place à la HP-92, fonctionnant entièrement sur piles, en 1977.
La HP-65 (1974) évoluera en HP-67 (1976) avec les technologies du moment (elle est donc électroniquement plus proche des modèles 21 et 25). Cette dernière est aussi déclinée en modèle de bureau à imprimante : HP-97 entièrement compatible !

Avant cela, il y aura les HP-55 (1975) et HP-25 comme déclinaisons moins chère avec plus de fonctions mathématiques mais sans carte de stockage, d’où un moindre attrait. Ce dernier modèle sera remplacé par les 19C (avec imprimante) et 29C (sans imprimante) en 1977, toujours pour des petits budgets.
On notera au passage que, encore une fois, le concurrent sort la tête longtemps après avec sa TI-59 (1977) qui propose enfin de pouvoir sauvegarder les programmes sur une carte amovible et offre assez de mémoire pour être une alternative crédible et compenser le nombre plus réduit de fonctions.
| HP-65 | HP-55 | HP-25 | HP-67 | HP-29C | TI-58 | TI-59 | |
|---|---|---|---|---|---|---|---|
| année | 1974 | 1975 | 1975 | 1976 | 1977 | 1977 | 1977 |
| extension | oui | non | non | oui | non | non | oui |
| pas de programme | 100 | 50 | 49 | 224 | 98 | 0—480 | 480—160—960 |
| registres mémoire | 9 | 20 | 8 | 26 | 30 | 60—0 | 60—100—0 |
| mémoire RAM (octets) | 480 | 1024 |
Les toutes premières générations, 9100A et 9100B vont être remplacé dès 1971 par HP-9810A avec un affichage diodes trois lignes au lieu du tube cathodique et à bien des égards va préfigurer la mythique HP-41C. En 1976 sortira HP-9815A qui sera remplacé en 1980 par HP-9815S et qui se distinguent par un affichage uniligne et le lecteur de cartes remplacé par un lecteur de bandes cassettes…
fonctionnalités
La fascination pour ces modèles intermédiaires viennent probablement de ces petits détails qui font des évolutions notables et pourtant plus abordables. L’ajout de nouvelles fonctions sans explosion du nombre de touches se fait par l’ajout de touche(s) de bascule (comme le « Shift » ou le « Alt Gr » sur un clavier d’ordinateur) ; ce qui est aussi d’un intérêt historique indéniable car c’est la première marque à utiliser ce procédé (en fait généralisé en 1973 avec les modèles 80 et 45, et qui sera rapidement copié par tous les autres constructeurs)
fonction | r.c HP-35 | r.c HP-21 |
|---|---|---|
arc sin | 2.3 arc sin | 1.2 🟦 SIN |
arc cos | 2.4 arc cos | 1.3 🟦 COS |
arc tan | 2.5 arc tan | 1.4 🟦 TAN |
lg e | 1.3 ln | 2.3 🟦 eˣ |
lg ⒑ | 1.2 log | 2.4 🟦 STO |
X pow. Y | 1.1 yˣ | 1.1 x≷y 🟦 ¹/ₓ |
Y pow. X | 1.1 x≷y yˣ | 1.1 🟦 ¹/ₓ |
⒑ pow. X | -.- | 2.5 🟦 RCL |
sqr. root | 2.1 √𝑥 | 3.3 🟦 CHS |
clear all | 1.5 CLR | 3.5 🟦 CL𝑋 |
pi | 8.4 π | 3.4 🟦 EEX |
reg. sub. | -.- | 4.1 🟦 - |
reg. add | -.- | 5.1 🟦 + |
reg. mul. | -.- | 6.1 🟦 × |
reg. div. | -.- | 7.1 🟦 ÷ |
disp.form. | -.- | 7.4 DSP |
to rect. | -.- | 2.2 🟦 x≷y |
to polar | -.- | 2.1 🟦 R⬇ |
Comme écrit dans « The Peninsulan » d’août 1975 :
Replacing the 35 in the division’s product line is the HP-21 —which, thanks to evolving technology, performs more functions for a lower price.
Mais j’avoue que, tant qu’à investir dans une antique HP, je préfèrerais une HP-45 (1973) qui a bien plus de fonctions de conversions (et était plus chère que la HP-21, mais devrait se trouver en occasion au même prix) surtout. Ou une HP-27 pour bénéficier des avancés faites entre deux. Bref, la HP-21 n’est pas banale quand on l’inscrit dans son histoire/époque, même si on n’aime pas trop le style Woodstock (et/ou sa tenue en main). Par contre, elle est largement dépassée on est d’accord.

Il y a un vrai reproche qui n’est pas mentionné : les notations sin⁻¹ / cos⁻¹ / tan⁻¹ !
Pour la comparaison avec le concurrent de même nationalité, Texas Instruments, il faut noter qu’à fonctionnalités (presque) équivalentes, leurs modèles sortent un an plus tard…
| HP | TI | HP |
|---|---|---|
| 35 | SR-10/SR-11 ? | 80 & 45 |
| 45 | SR-50 | 21/46 & 91 |
| 80 | SR-51 | 70/81 & 22/92 |
| 65 | SR-52 | 55 & 25 |
| 55 | SR-56 | 27/67 |
| 67 | TI-59 | 97/41 |
| 25 | TI-58 | 29C/19C & 95C |
Les SR-10 et SR-11 avaient la notation scientifique et trois fonctions de base (carré, racine carré, inverse) ; mais il a fallu attendre la SR-50 (1974) pour avoir aussi les fonction trigonométriques et logarithmique et donc correspondre vraiment à une calculatrice scientifique. Fait notable et remarquable, elle offrait aussi le calcul de factorielle (présente aussi sur les HP-45 et HP-55 mais pas sur les HP-21 et HP-25 hélas) et les fonctions hyperboliques (que je ne crois pas avoir vu en poche avant le HP-32E mais qui se programmaient en six touches) Entre temps, Compucorp avait sorti (en 1972) deux calculatrices scientifiques, 322G Scientist et 324G Scientist faits avec des cartes Texas Instruments mais ne convenait que pour de larges poches (assez petit pour des calculatrices de bureau mais occupant presque deux fois plus de place que la HP-35, et pas toujours pratique pour certains calculs je trouve, mais ils ont tenté de relever le défi.)
Je vais m’arrêter sur quelques fonctionnalités notables qui ne sont pas de l’ordre des fonctions intégrées supplémentaires et qui sont marquants de mon point de vue.
affichage…
Bon, la réduction de taille implique celle de l’affichage (qui devient plus dynamique) tout en gardant la même précision :
In spite of the shorter display, there was still a requirement that the calculator have ten-digit precision. To meet this requirement, the decimal point was moved so that it appears next to a digit. Also, a decision was made to show a maximum of eight mantissa digits when an exponent is displayed, so two of the display digits do double duty, sometimes as mantissa digits, and other times as exponent sign and digit.
Je résume cette évolution dans le tableau suivant :
| 1972 | 1975 | chiffres |
|---|---|---|
| 15 | 12 | total |
| 10 | 8 ou 10 | mantisse |
| 2 | 2 ou 0 | exposant |
| 0 à 2 | 0 à 2 | signe |
J’aime bien la nouvelle façon d’afficher qui ne ressemble plus à ce qui se faisait sur les calculatrices mécaniques. J’aime aussi le remplacement de la touche yˣ par xʸ et la touche DSP (pour « display ») qui permet de gérer le nombre de décimales affichées (et donc l’arrondi final.)
Les calculatrices de bureau de la marque et la calculatrice de poche HP-21 affichent par défaut deux chiffres après la virgule, tandis que la HP-35 n’affiche pas de zéro. Mais tous les calculs sont toujours fait avec toute la précision disponible (soit quinze chiffres pour la HP-35 et la HP-9100 par exemple, et douze pour la HP-21, on l’aura compris), seule l’affichage est dynamique, ce qu’on ne trouve pas chez la concurrence pendant longtemps (1976 si j’ai bonne mémoire.)
| calcul de | affichage HP-21 | affichage HP-35 | type |
|---|---|---|---|
1582000*1842 |
291404000 |
291404000 |
décimal (normal) |
1582000*18420 |
2.9140440 10 |
2.914044 10 |
scientifique (2.914044E+10) |
Évolution par rapport au HP-35, apparue avec la HP-45, on peut de nouveau contrôler l’affichage comme sur les calculatrices de bureau. On peut choisir l’affichage décimal avec un nombre de chiffres significatifs.
saisie HP-21 | affichage HP-21 |
|---|---|
1 2 3 . 4 5 6 7 Enterꜛ |
|
par défaut (noter l’arrondi automatique) | |
DSP . 4 |
|
DSP . 6 |
|
zéros surnuméraires (valeur exacte toujours manipulée en mémoire) | |
DSP . 2 |
|
DSP . 0 |
|
On peut de même opter pour l’affichage scientifique avec un nombre donné de décimales, en faisant automatiquement l’arrondi pour nous : la mantisse est toujours justifiée à gauche et sur huit chiffres (sur les calculatrices de bureau le point décimal est en position fixe avec autant de place de part et d’autre pour la mantisse et c’est d’un bel effet), tandis que l’exposant est justifié à droite toujours sur deux chiffres.
saisie HP-21 | affichage HP-21 |
|---|---|
1 2 3 . 4 5 6 7 Enterꜛ |
|
DSP 2 |
|
DSP 4 |
|
DSP 7 |
|
DSP 8 |
|
…saisie
C’est aussi la seule marque sur laquelle on a une saisie un peu dynamique, et surtout le premier constructeur qui introduit la notation scientifique déjà évoquée. Elle sera aussi la seule dont les calculatrices en font usage jusqu’en 1976 en gros.
C’est fièrement signifié par la touche enter exp (pour « enter exponent ») sur les modèles de bureau, et E EX sur HP-35 (l’espace disparaîtra sur les modèles de poche suivants.) Pour saisir quinze virgule six trillion, là où on doit appuyer douze fois sur 0 ou au mieux six fois sur 00 sur les calculatrices de l’époque, ça devient simplement (trois touches)
saisie | affichage HP-21 | |
|---|---|---|
1 5 . 6 |
| affichage normal |
E EX |
| bascule en mode scientifique |
1 2 |
| saisie de l’exposant |
Enterꜛ |
| affichage scientifique |
2 5 × |
| affichage normal |
La simplification est poussée assez loin pour une nouveauté et pour l’époque. Prenons par exemple le calcul du million réparti en cinquante deux
saisie | affichage HP-21 | |
|---|---|---|
CL𝑋 |
| condition de validité ce qui suit |
E EX |
| pas besoin de saisir |
6 |
| puissance six pour le million |
Enterꜛ |
| affichage normal par défaut |
5 2 ÷ |
| affichage normal si possible |
DSP 6 |
| affichage scientifique explicite |
Il y a par contre une petite subtilité pour les exposants négatifs, comme lorsqu’on veut prendre cinquante quantum d’action
saisie | affichage HP-21 | |
|---|---|---|
6 . 6 2 5 |
| mode normal |
E EX |
| passage en saisie scientifique |
CHS |
| activation puissance négative… |
2 7 |
| valeur absolue de la puissance… |
Enterꜛ |
| affichage scientifique implicite |
5 0 |
| affichage normal par défaut |
× |
| affichage scientifique implicite |
Et il y a malgré tout quelques limitations :
- Quand la mantisse a plus de huit chiffres avant la virgule, le mode de saisie scientifique est désactivé. Ainsi, pour
123456789.1E23il vaut mieux saisir12345678.91E24 - On ne peut pas utiliser le mode de saisie scientifique quand le premier chiffre significatif arrive après la huitième position. Ainsi, pour
0000.000025E55il vaut mieux saisir0000.00025E54ou0.000025E55
Ce n’est cependant pas mal et surtout c’était les seuls à savoir faire cela.
etc.
La HP-45 (1973) est la première calculatrice à proposer la touche Last 𝑋 (ou LST𝑥 sur certains modèles) : la sauvegarde de ce niveau avant toute opération est un must qui n’est pas sur les modèles 21 et 91 mais sera systématique à partir de 1975. C’est aussi la première calculatrice à proposer une touche 𝑥² qui sera reprise plus tard par quasiment tout le monde. Ce modèle introduit le formatage d’affichage (évoqué plus tôt), pour la première fois, sur les calculatrices de poche. C’est aussi le premier constructeur, et le seul pendant fort longtemps, à offrir la conversion d’unités (c’est le genre de truc qui fait défaut sur des TI au même prix qu’un modèle HP après lequel il sort.)
La HP-55 (1975) en plus d’offrir plus de conversions, a un timer exploitable (ça y était déjà sur la 45 mais pas facilement accessible) et bien pensé pour avoir dix chronomètres. Programmable aussi, elle introduit une autre forme d’adressage et de saut, mais surtout l’exécution pas-à-pas (utile aussi bien pour la recherche de bogue que pour aider à la mise au point.) Des fonctionnalités qu’on retrouvera sur de nombreux autres modèles et qui sont encore absent chez beaucoup de concurrents aujourd’hui.
La HP-25 (1975) est le premier modèle à proposer officiellement le mode d’affichage ingénieur. C’est aussi la première à subir une mise à niveau et non un remplacement complet. Cela donna la HP-25C (1976) qui est une révolution devenu un critère non négociable aujourd’hui : l’usage de la technologie de mémoire CMOS qui permet de ne plus faire de reset au moment de changer les piles…
La HP-34C (1979) est la première calculatrice de poche à faire du calcul numérique d’intégrale et la recherche de zéro de fonction. Il faudra des lustres pour voir arriver ces fonctionnalités, disponibles depuis le début sur leurs calculatrices de bureaux, sur d’autres calculatrices de poche. C’est aussi la première calculatrice qui implémente la fonction gamma sur les réels.
La HP-15 (1982) est la première calculatrice, à ma connaissance, à faire du calcul de complexes (et ce fut le seul constructeur pendant longtemps) et de matrices numériques (celui là sera par contre repris par la plupart des calculatrices graphiques dès 1990.)
La HP-28C (1987) est la première calculatrice graphique du constructeur, mais sur ce coup ils sont en retard vu que le concept est apparu avec Casio fx-7000G (1985) presque deux plus tôt. Mais pas plus en retard que le texan qui mettra encore trois ans avant d’arriver sur ce marché avec sa TI-81 (1990) qui utilise le même circuit que Casio… La fx-7000G n’avait que 82 fonctions (moins que ce que propose les HP en 1980…) et disposait de deux touches de bascule (« shift » orange et « alpha » rouge) —concept largement éprouvé chez HP.
La HP-28C reprend et améliore leur outil de résolution numérique et leur navigation par menus, tous deux introduits avec la HP-18C (1986). Ce type de menu sera repris par la seconde génération de graphiques Casio (i.e. 9750/9850/9950/9970 et leurs variantes) dès 1996 (soit dix ans plus tard) où on voit apparaitre les touches « F1 » à « F6 » !
Sur ce modèle, la conversion d’unités est encore plus aboutie et complète, il y a les opérations sur bits comme sur HP-16C mais sans devoir rentrer dans un mode dédié, il y a un catalogue d’aide comme sur HP-41C mais avec plus de confort, etc.

Son évolution, HP-28S (1988) offre plus de mémoire (on passe de 2K à 32K) ainsi que le menu perso et l’arborescence de variables.
La liste pourrait se poursuivre comme ça sur plusieurs pages, et cela suffit pour que la marque soit source de fascination, que l’on aime ou pas ses produits. Et pourtant, je ne suis pas en train de claironner comme des fans et zélotes que cette entreprise a tout inventé, pour preuve j’ai fait remarqué : qu’on ne lui doit pas la première calculatrice de poche, ni l’usage du LCD (elle fut cependant parmi les premières connues du grand public), qu’on ne lui doit pas la première calculatrice graphique (il s’en ai fallu de peu mais ce n’était pas la direction vers laquelle tendait ce constructeur), qu’elle n’a pas proposé de fonctions hyperboliques pré câblées pendant longtemps, etc.
vive la NPI
Concernant la NPI (RPN en anglais), apparue avec le modèle 9100A à la fin des années 1960, (en vérité, Hewlett-Packard lui a surtout donné son nom, en hommage aux travaux, en 1924, du mathématicien/philosophe/logicien polonais Jan Łukasiewicz, mais le concept peut être retrouvé sur la calculatrice mécanique danoise Bonh Contex de 1957…)
pourtant plus naturel
Elle me semble justement accessible « à la main non éduquée » (si j’ai bien compris, c’est une formulation ironique ou métaphorique pour désigner les personnes qui n’ont pas fait de hautes études ?) car correspondant à la façon dont nous avons justement appris à « calculer » sans machine (i.e. avec le crayon sur le papier ou le bout de craie sur le tableau —in fine, une main éduquée), en tout cas en ce qui me concerne… Exemple simple de mise en bouche :
Hormis le fait de poser les unités/dizaines/centaines/milliers/etc. les uns sous les autres ; on remarquera qu’il y a virtuellement un tableau avec une colonne des nombres manipulés et une colonne des opérations entre eux. Quand on passe la colonne des opérateurs à droite, comme sur HP-97 et les actuelles calculatrices imprimantes, on voit que la NPI suit cette manière de faire naturelle (pour les dinosaures…?)
nombre | opérateur |
|---|---|
4 5 | Enterꜛ |
2 1 8 | + |
8 0 0 | + |
C’est la façon de fonctionner aussi des machines arithmétiques d’avant (du moins sur celles que j’ai eu à tester)
nombre | opérateur |
4 5 | += |
2 1 8 | += |
8 0 0 | += |
Même chose pour les autres opérations, sauf que les retenues et additions (ou soustractions) intermédiaires pour les multiplications (ou les divisions) ne sont pas affichées, et on n’a pas le reste de la division.
En voulant vérifier si l’évolution des programmes a changé l’enseignement de la façon de faire, j’apprends que la bonne vieille méthode est dite justement en colonne et qu’il y a également une nouvelle méthode dite en ligne —que je trouve moins simple mais bon ce doit être l’inaptitude ? me demande quand même si ce n’est pas pour ça que les nouvelles générations ne peuvent plus se passer de calculettes mais je digresse.
stratégies exécutoires
Il convient de faire un petit détour par le fonctionnement interne, sans devoir être technique, promis.
exécutions immédiates
L’approche des calculatrices RPN reste l’exécution immédiate (dite « single-step » ou « immediate-execution » ou encore « chain calculation ») comme sur les calculatrices ultra simples (dites « quatre opérations ») ou parfois plus évoluées (dont des modèles scientifiques) comme on en trouve chez de nombreux constructeurs
- Sharp (les véritables premières calculatrices de poche) et sa notation Ten Key
- QT-8D (1969)
- QT-8B (1970)
- EL-8 (1970)
- à noter que la marque continue de produire des calculatrices comptables selon ce concept (nom déposé), comme le QS-2770H, et à noter aussi la HP-10 sortie en 1977 qui utilise le même principe repris aussi un temps par Casio.
- Texas Instruments
- SR-50 (janvier 1974) et SR-51 (1974) tous deux avec des fonctions trigonométriques et logarithmiques.
- TI-150 (décembre 1974) avec en plus %
- TI-1200 et LADY 1200 (mars 1975) avec en plus %
- TI-1400 (1976) avec en plus % et ±
- TI-1030 (juin 1978) avec en plus % et √
- TI-1070 (juin 1978) avec en plus %, √, ±, 𝑥², ¹/ₓ
- TI-1071 (1979) avec en plus %, √, ±, 𝑥², ¹/ₓ
- TI-1760 (août 1979) avec en plus √
- TI-1010 (1979) avec en plus √ et %
- TI-1031 (1981) avec en plus % et √
- TI-1001 (avril 1982) avec en plus % et √
- TI-1002 (1983) avec en plus % et √
- TI-1036 (1983) avec en plus % et √
- TI-1786 (1985) avec en plus % et √
- Elektronika
- B3–11 (1976)
- B3–14M (1976) avec en plus √ et ¹/ₓ
- B3–09M (1979) avec en plus % et ¹/ₓ
- B3–21 (1979) scientifique complète et programmable
- B3–39 (1979) avec en plus √ et %
- B3–14 (1980) avec en plus √, %, ¹/ₓ
- B3–34 (1979) scientifique complète et programmable
- Addmaster
- National Semiconductor electronics
- NS 600 sans .
- Novus 650 Matchbox sans . (et qu’on retrouve également comme Montgomery Ward P10 ou Accuron 600 et probablement d’autres noms)
- Novus 950, sans .
- Sinclair Radionics
- Executive (août 1972) sans . mais avec EEX
- Scientific (1974) avec en plus les fonctions trigonométriques et logarithmiques
- Scientific programmable (1975) avec les fonctions trigonométriques et de la mémoire de programmation de 24 pas
- les systèmes d’exploitation
- Windows en mode standard, avec en plus ±, %, √, 𝑥² et ¹/ₓ
- MacOS en mode basic, avec en plus ± et %
- gcalctool en mode basic
- etc.
- et de nombreux autres
- Commodore 4921 (1976) qui a toutes les fonctions du Commodore 4190…
- Commodore Minuteman ★ 6 (1974) sans .
- American 1776 (1976) sans .
- Privileg beginner sans .
Dans cette approche, les opérations sont (immédiatement) déclenchées par l’appuie d’une touche et on calcule au fur et à mesure tous les résultats intermédiaires jusqu’au résultat final. (on peut le voir dans le premier exemple, où l’on voit d’abord la somme de 45 et 218, puis celle de 263 et de 800 enfin.) Dans ce mode (chain calculation) on note trois écoles :
- des nombreuses, comme la SR-50 de TI, qui utilisent un mélange de
- notation « infixée » (pour les opérations duales que sont les quatre opérations de base ainsi que celui de calcul de pourcentage et plus tard les arrangements/permutations de probabilité de tirages, ou encore les comparaisons logiques ; dans ce cas, l’opération est en attente de la saisie de la seconde opérande dont la fin de saisie est signalée par une autre touche d’opération et on reboucle)
- et de notation « suffixée » (pour les opérations unaires tels que : la puissance carré, la racine carrée, le changement de signe ou négation, la puissance inverse ou inversion, le factoriel, le sinus, le cosinus, la tangente, les logarithmes, l’exponentiel, les conversions…)
- quelques anciennes, et quelques nouvelles (cas vu chez Casio), utilisent un mélange de
- notation « infixée » (pour les opérations à deux arguments)
- et de notation « préfixée » (pour les opérations à un seul argument)
- les nouvelles, RPN, qui n’utilisent que la notation « suffixée » et sont donc plus cohérentes (et simples à mon goût) et moins déroutantes
Les exemples suivants montrent ces différences chez quelques éditeurs, en 1975, pour des calculs simples.
HP | Sharp | TI | NS&S | |
|---|---|---|---|---|
Clear | C | C | C C | |
2 1 | Enterꜛ | += | + | + |
3 7 | + | += | = | + |
21+37 en 1975HP | Sharp | TI | NS&S | |
|---|---|---|---|---|
Clear | C | C | C C | |
3 1 | Enterꜛ | ×÷ | × | + |
2 7 | × | += | = | × |
31×27 en 1975HP | Sharp | TI | NS&S | |
|---|---|---|---|---|
Clear | C | C | C C | |
1 7 | √ | n/a | √ | n/a |
√17 en 1975Ça va quand on se limite aux quatre opérations, mais bonjour les nœuds au cerveau quand on commence à combiner.
calcul | HP-35 et tout RPN | ou (commutativité) | TI SR-50 |
|---|---|---|---|
| 2 Enterꜛ 1 8 √ × | 1 8 √ 2 × | 2 × √ 1 8 = |
| 3 Enterꜛ 3 0 SIN × | 3 0 SIN 3 × | 3 × SIN 3 0 = |
L’évaluation immédiate est, électroniquement, le mode de fonctionnement le plus simple et le plus rapide ; les autres formes d’évaluation s’y ramènent au final (mais il s’agit là de détails d’implémentation qui n’intéressent pas les usagers finaux.) C’est aussi le mode de fonctionnement historique pour la bonne raison que l’affichage était sur une seule ligne utilisant des blocs sept segments à diodes ; du coup, on ne pouvait afficher que des nombres…

exécution différée
L’évaluation différée existait déjà sur les ordinateurs et la notation dite « algébrique » (qui au passage n’est pas exactement celle de l’algèbre si on veut être honnête) a été introduite par le langage de programmation ForTran. Pour être utilisable sur une calculatrice il fallait attendre l’arrivée de l’écran à cristaux liquides (où l’on peut afficher plus de symboles) ainsi que l’augmentation de la puissance de calcul des puces (plus exactement plus la taille se réduit et plus on peut embarquer de vitesse ou de capacités dans la main) ; du coup on peut entrer des formules en les voyant s’afficher, puis valider avant que le calcul soit lancé. S’il y a deux lignes ou plus, l’une servira pour afficher la saisie et l’autre pour le résultat ; et s’il n’y a qu’une ligne (rare mais possible) elle servira pour entrer la formule puis pour afficher le résultat.

Il ne s’agit pas d’opposer les deux modes de traitement qui ont chacun leurs avantages et leurs inconvénients (il est biaisé de ne voir que les points forts de l’un et les points faibles de l’autre, raison pour laquelle je peux expliquer et défendre la RPN sans devoir taper sur les autres.) Je pense que la supériorité (apparente ?) de la RPN est lié à son côté plus naturel (évoqué un peu plus tôt) et plus simple pour des calculs longs (comme ce sera illustré plus loin), mais les études que j’ai trouvées —comme celui de Kees Vandersanden par exemple— ne font que constater sans donner d’explication.
non exclusivités
…chez HP
Par ailleurs, je ne sais pas d’où vient l’idée reçue que Hewlett-Packard c’est forcément la notation polonaise inversée : cette marque a aussi proposé des modèles qui
- n’utilisent que le mode algébrique (appellation chez eux, mais aussi : AOS chez Texas Instruments, DAL chez Sharp, VPAM chez Casio, BASIC pour moi car rappelant la façon d’écrire les formules dans ce langage… utilisé par : HP-75C/HP-75D, HP-71, Sharp PC-1211, Casio FX-702P, Sharp PC-1500, Casio PB-xxx, etc. Pour la suite, afin de ne pas faire de pub/prosélytisme, j’emprunterai l’appellation AESH/AESP à John A. Ball dans son ouvrage de 1978, « Algorithms for RPN calculators », chez Wiley-interscience.) comme les modèles
- 9820A en 1972 (leur première de bureau à utiliser cette logique)
- 9805 en 1973 (leur plus petite, non programmable, et la moins chère de bureau spécialisée en statistiques)
- 01 en 1977 (leur montre-calculatrice résistante aux chocs usuels et à l’immersion dans dix mètres pendant cinq minutes, elle était capable de faire divers calculs de dates)
- 10 en 1977 (leur quatre-opérations de poche avec imprimante et saisie/affichage monétaire, pourcentage et opérations sur mémoire annexe)
- 18C en 1986 (leur première financière de poche à utiliser cette logique)
- 17B en 1988 (leur seconde financière de poche à utiliser cette logique, avec une pile d’historique et un menu), puis les 19B/10B/10BII/14B
- 22S (leur première scientifique de poche à utiliser cette logique) et 27S (un générique —scientifique capable de stats— qui utilise cette logique, avec une pile d’historique) en 1988
- 20S et 21S en 1989
- 30S en 1990
- 38G en 1995 (leur première graphique à utiliser cette logique), puis 39G/40G/39G+
- proposent les deux modes (AESH/AESP et RPN par défaut) comme les
- 28C en 1987 (sera remplacé, l’année suivante, par le 28S ; toutes deux sont les ancêtres de la série graphique 48/49 et de la pile de taille illimitée)
- 17BII et 19BII en 1990, puis 17BII+ en 2003
- 32SII en 1991, puis 33S en 2003
…des NPI
Enfin, beaucoup l’ignorent mais de nombreux autres constructeurs ont produit des calculatrices fonctionnant en RPN ; voir par exemple sur les sites gschwaninger.de et thimet.de entre autres. C’est juste que les autres n’ont jamais pu surpasser la référence (comme le montre par exemple l’analyse du Sinclair Scientific par Ken Shirriff —qui est cependant une belle prouesse à sa façon…) d’où la fascination ?
Pour la petite histoire, l’appellation RPN est le fait de Hewlett-Packard qui l’a popularisé, mais le principe a été théorisé en 1951… et a été implémenté dans les calculatrices de bureau à transistors de Friden dès 1963 ! (ce n’était juste pas nommé et leur manuel parlait de système basé sur une pile…)

balle de match
Trêve de bavardage, prenons un autre exemple moins simple mais fort facile
évaluation immédiate
Dans le mode d’évaluation immédiate, qui est comparable à la programmation impérative, et où on fait le calcul naturellement (comme on le ferait à la main), il ne faut pas oublier que la multiplication doit être prioritaire sur l’addition :
- En utilisant le mix infix-préfix, il faut saisir : « 2 × 3 + 1 » (il faut d’abord faire
2×3puis6+1qui est pareil que1+6. En saisissant naïvement « 1 + 2 × 3 » on aurait fait au fur et à mesure1+2puis3×3ce qui donnerait9au lieu du7attendu…) - En utilisant le postfix, il faut saisir : « 2 Enterꜛ 3 × 1 + » (même raisonnement que précédemment : on fait d’abord la multiplication, puis ensuite l’addition) ; mais il est aussi possible, en utilisant la pile, de faire plutôt : « 1 Enterꜛ 2 Enterꜛ 3 × + » (dans la première on termine par
6+1et dans la seconde on termine par1+6en ayant entré les nombres dans leur ordre d’apparition.)
évaluation différée…
Dans le mode d’évaluation différée, qui est comparable à la programmation déclarative, et où on va formuler le calcul à faire…
- Il existe de nombreux languages (APL, Smalltalk, OCaml, Mary), et quelques calculatrices, qui ne gèrent pas les priorités (ou très peu), et il faut alors rajouter des parenthèses (qui ont toujours la plus haute priorité garantie) : « 1 + ( 2 × 3 ) = » (ici aussi, on a une réécriture sous la forme
1+(2×3)pour ne pas obtenir9contre toute attente…) - De plus en plus, ces règles de priorité sont intégrées dans les calculettes et on peut simplement écrire : « 1 + 2 × 3 = »
…fort difficile
Ne pas avoir à réfléchir où poser des parenthèses est le principal attrait de la RPN, un autre étant de ne pas avoir à réécrire/réarranger les termes (ce qui rend le flux de travail plus rapide et plus simple pour les moins experts/expertes.) On parle aussi du moindre nombre de touches requis mais je pense que c’est quasiment équivalent en moyenne… Quand la notation infixée est directement donnée, les calculatrices l’utilisant semblent plus simple car il faut juste recopier ce qu’on lit. Sauf que ça ne marche que pour le mode de calcul différé et connaissant les règles de priorité : la calculatrice Windows répond 9 en vue standard et 7 en vue scientifique ou programmeur. Même en mode de calcul différé, avec application de PEMDAS (Parenthèses, Exposants, Multiplication/Division, Addition/Soustraction) ou BODMAS/BIDMAS/BEDMAS/KlaPoPuStri/etc, il y a des cas qu’il faut préciser par des parenthèses supplémentaires sinon la calculatrice a sa compréhension légitime :
a^b^cs’interprète commea^(b^c)par TI-92 et TI-30XS MultiView en vue Mathprint(a^b)^cpar TI-30XII et TI-30XS MultiView en vue Classic
a÷(bX)(par exemple1/2x) eta÷b(c±d)s’interprètent commea÷(b×X)(i.e.1÷(2x)) eta÷b×(c±d)par TI-82 et de nombreuses Casio actuelles dont les fx-??MS/fx-???MS et les fx-???ES(a÷b)×X(i.e.(1÷2)x) eta÷(b×(c±d)par TI-83 et les TI graphique à partir de 1996, les Casio fx-???ES+, ainsi que les HP en mode algébrique qui suivent la pratique de Maple et Mathematica
En RPN, toutes ces considérations qui ont fait s’arracher des cheveux à des étudiants ou engendré des discussions enflammées sur les réseaux sociaux, n’ont plus lieu d’être puisqu’on décide exactement ce qu’on fait comme calcul. Quelques exemples concrets pour la route :
16/4/4peut s’interpréter comme(16÷4)÷4 = 1(left associative) ou16÷(4÷4) = 16(right associative)
6÷2(1+2)peut s’interpréter comme6÷(2×(1+2)) = 1(priorité supérieure pour la multiplication implicite) ou(6÷2)×(1+2) = 9(la division et la multiplication sont au même niveau et calculé dans l’ordre d’apparition)
8/2(2+2)peut s’interpréter comme8÷(2×(2+2)) = 1(priorité supérieure pour la multiplication implicite)(8÷2)×(2+2) = 16(multiplication implicite traitée de manière égale)
9÷3(1+2)peut s’interpréter comme9÷(3×(1+2)) = 1(priorité supérieure pour la multiplication implicite)(9÷3)×(1+2) = 9(multiplication implicite traitée de manière égale)
-2^4peut s’interpréter comme(-2)^4 = 16comme on l’a appris (en tout cas comme je ferais naturellement)-(2^4) = -16comme certains tableurs (dont Microsoft Excel et LibreOffice Calc entre autres)
48÷2(9+3)qui peut signifier48÷2×(9+3) = 28848÷(2×(9+3)) = 2
On peut trouver d’autres exemples comme cela… Les occasions de se louper (et/ou s’écharper sur les réseaux asociaux) ne manquent pas mais faut pas le dire.

Encore une fois, le propos ne vise pas à taper sur les calculatrices dites algébriques (pas juste à notation infixée comme peuvent l’être aussi des calculatrices à évaluation immédiate) ; au contraire elles sont bien pratiques quand on n’a qu’à recopier la formule (les livres de maths de collèges/lycées que j’ai feuilleté indiquent la marque et le modèle pour laquelle les entrées sont destinées …ce qui en fait des canaux de pub qui ne disent pas leur nom.) En dehors de ce contexte, il ne faut point croire que c’est plus fastoche, et il convient de potasser le chapitre ou l’annexe des priorités …parce-que les conventions ne sont pas figées dans le marbre et qu’il faut toujours « lever l’ambiguïté en ajoutant des parenthèses » Les conventions utilisées sont explicites en RPN et on n’a pas recours aux parenthèses.
Au moment de boucler, je vois qu’il y a une page Wikipédia nommée « Ordre des opérations » qui reprend ces points et dont je recommande la lecture.
pile NPI
Comme promis, parlons de la pile. Le sens premier est celui de l’empilement (de choses). C’est aussi pour cela que les batteries électriques sont abusément nommées ainsi (en fait c’est une traduction littérale l’anglais battery) Dans le cas de la RPN, c’est un empilement de casiers comparable à celui bien connu des bannettes, sauf qu’ils contiendront seulement un nombre (i.e. registre de donnée du processeur…)
En informatique, on emploie deux mots selon la façon dont on va manipuler et gérer l’entassement :
- tas ou « heap » qui fonctionne sur le principe du « premier entré, premier sorti » (ou « PEPS ou FIFO »)
- pile ou « stack » qui fonctionne sur le principe du « dernier arrivé, premier sorti » (ou « DEPS ou LIFO »)
- file ou « queue » qui est un synonyme de la pile.
Comme on va le voir, la taille (i.e. nombre de niveaux) de la pile va déterminer la puissance de calcul.
2 niveaux
Il en faut au moins deux, et c’est la taille de la pile des calculatrices Sinclair et Commodore.

Deux niveaux sont suffisant pour la plupart des calculs :
- un premier niveau dit de saisie ou d’affichage car c’est là que s’affiche le nombre que l’on saisie,
- un second niveau dit de stockage temporaire ou d’accumulation car c’est utilisé pour garder un deuxième argument d’une opération.
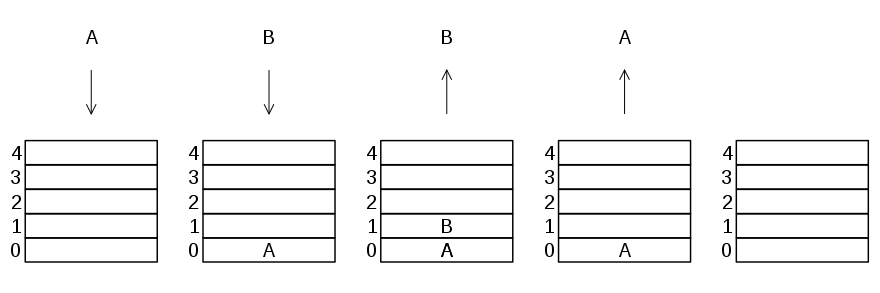
Voyons comment cela se passe, sous le capot, avec une variante d’un exemple précédent
Au départ, la contenu de la pile est vide, sinon il faut appuyer sur Clear :
affiché | mémorisé | saisie suivante | explication | |
|---|---|---|---|---|
1 | 1 | Toute saisie se fait dans le premier niveau de la pile | ||
2 | 1 | Enterꜛ | L’appuie sur Enterꜛ pousse dans le second niveau | |
3 | 1 | 1 | 3 | La saisie suivante va dans le premier niveau, ça ne change pas |
4 | 3 | 1 | + | Comme déjà dit, une opération dyadique va utiliser les deux premiers arguments de la pile (autrement dit |
5 | 4 | 2 | On poursuit la saisie avec le nombre suivant… | |
6 | 2 | 4 | × | …puis l’opération (soit |
7 | 8 | le résultat est toujours posé dans le niveau bas, le premier |
Dans cet exemple, on voit comment deux niveaux suffisent pour faire tout le calcul, comme il se présente, avec trois termes et deux opérateurs.
Avec les autres calculatrices quatre opérations équivalentes de l’époque (petite liste ci-après), il aurait fallu procéder en deux temps pour celles en évaluation directe (non, non, l’utilisation de la mémoire/touche Ans n’est arrivée que dans les années 1990 — TI-83, Casio fx-7000G, etc.)
- Canon Pocketronic (1970)
- Sharp QT8 (1970)
- Texas Instruments LP-3000 (1972) — une des premières de bureau ?
- Texas Instruments TI-2500 (1972) — qui était quand même à cent cinquante dollars
- Casio MINI CM-602 (1973)
- Aristo M 27 (1973) — version 3
- Pulsar (1975) — première montre calculatrice
- Sharp EL8026 (1976) — première calculatrice solaire
- Texas Instruments TI Little Professor (1976)
Pour la formule de traitement différé il aurait fallu rajouter des parenthèses, pour ne pas procéder en deux temps, et c’est dans ce genre de cas qu’on a plus de touches (dans ce calcul simple ce n’est pas pénalisant, le plus important étant surtout de ne pas oublier de parenthéser.) Noter au passage que des bêtes de calcul comme les TI SR-50 et SR-51 ne savent pas effectuer ce calcul simple d’une traite… (en l’absence de parenthèses et avec AESH/AESP, il faut donc calculer séparément l’addition puis faire la multiplication dans un second temps…)
notation | compte | touches appuyées |
|---|---|---|
RPN | 6 | Clear 1 Enterꜛ 3 + 2 × |
A-chain/AESH | 6 | Clear 1 + 3 × 2 Enterꜛ |
BASIC/AESP | 8 | Clear ( 1 + 3 ) × 2 Enterꜛ |
3 niveaux
HP-9100 et HP-9810 proposent trois niveaux ou registres (casiers à nombre d’après mon analogie) nommés :
Xpour le registre « keyboard » (celui de saisie/affichage),YetZpour les registres « accumulator » (accumulateur principal) et « temporary » (accumulateur secondaire ou temporaire).

Le même exemple s’y transpose de la même façon (qui peut le plus peut le moins)
saisie | registre X | registre Y | registre Z |
|---|---|---|---|
1 | 1. | 0. | 0. |
Enterꜛ | 1. | 1. | 0. |
3 | 3. | 1. | 0. |
+ | 4. | 0. | 0. |
2 | 2. | 4. | 0. |
× | 8. | 0. | 0. |
Avec un registre en plus, on peut aller beaucoup plus loin (i.e. faire des calculs plus complexes d’une traite.) L’exemple suivant l’illustre bien.
Ici aussi, on va utiliser une pile de trois niveaux de façon intuitive.
saisie | registre X | registre Y | registre Z |
|---|---|---|---|
Clear | 0. | 0. | 0. |
1 5 | 15. | 0. | 0. |
Enterꜛ | 15. | 15. | 0. |
1 9 | 19. | 15. | 0. |
+ | 34. | 0. | 0. |
4 4 | 44. | 34. | 0. |
Enterꜛ | 44. | 44. | 34. |
7 | 7. | 44. | 34. |
- | 37. | 34. | 34. |
÷ | 0.918918918 | 34. | 34. |
Le résultat est ici tronqué (il manque trois chiffres, affichés par la HP-35 par exemple, mais on aura compris que c’est une période de 918). Mais les points importants à noter sont qu’avec la RPN :
- Pas besoin de notes intermédiaires, contrairement aux autres calculettes à évaluation directe (mais il y a un contournement pour ce genre d’exemple précis, on y reviendra)
- Pas besoin de parenthèses ou de règles imposées et pas toujours claires…
- On voit l’évolution du calcul, qui est donc transparent, et on lève les erreurs plus tôt (en fait cette méthode convient aux gens qui savent un peu calculer et n’attendent pas qu’une machine fasse de la magie et leur délivre un résultat)
- En contrepartie, on décide de sa stratégie de calcul, la calculatrice ne servant que d’assistante et non de substitut magique.
C’est un fonctionnement idéal, tel qu’on le retrouve sur les autres calculatrices RPN des années '70 et '80, qui est décrit ici. Les calculatrices de bureau HP de 1968 n’avaient pas un fonctionnement aussi cohérent : les opérations dyadiques renvoyaient leur résultat dans le registre Y… ; quelques opérations monadiques se font directement sur Y (touches |y|, Acc - et Acc +) contrairement à l’usage courant évoqué ; et la pile n’est pas automatiquement réorganisée après les opérations (outre les touches Roll↓ et Roll↑ d’une part, on avait aussi ↑ et ↓ d’autre part) et les opérations sur les variables concernaient les deux niveaux (d’où x→()/x←()/y→()/y⇄().)

(Enterꜛ/x≷y/R⬇ sont plutôt étiquetés ↑/x⇄y/Roll ↓)

Avec une pile de trois niveaux, en RPN on peut faire des calculs fort complexes d’une traite là où les calculatrices non-RPN ne peuvent simplement pas …même en utilisant la mémoire annexe qui sera évoquée plus loin. L’exemple suivant est pourtant fort simple il me semble : ; mais je vous défie d’y arriver avec la TI SR-50… CQFD.
mémoire annexe
Bon, l’évaluation immédiate non RPN et l’évaluation différée sans parenthèses n’ont pas dit leur dernier mot car certains modèles ont intégré un registre séparé à usage libre de l’utilisateur, avec les touches de type MRcl/MSto/MClr (où les deux premiers sont RCL/STO sur les HP-35 et HP-21 par exemple…) On peut citer, non exhaustivement, parmi les premières :
- Texas Instruments avec ses modèles :
- TI-1265 et TI-1450 (1976) avec %, ±, MC, MR, M-, M+.
- TI-2550 III (1976) avec %, ±, √, 𝑥², ¹/ₓ, RV, CM, MR, M-, M+.
- TI-1760 DataCard (août 1979) avec %, √, MR, MC, M-, M+.
- TI-1750 III (1982) avec %, √, MR, MC, M-, M+.
- TI-1755 et TI-1754 et TI-1756 (1982) avec %, √, π, MRC, M-, M+.
- TI-1706 (1983) avec %, √, MR, MC, M-, M+.
- TI-1755 SLR (1983) avec %, √, ±, large +, MC, MR, M-, M+.
- TI-108 (1986) avec %, √, ±, large =, MRC, M-, M+.
- Elektronika avec ses modèles :
- B3–24 (1978) qui a M+.
- B3–26 (1979) qui a M+ et M-.
- MK-53 (1986) qui a M+ et M-.
- Aristo avec ses modèles
- M 36 (1973) avec ses touches %, xy et M.
- M 75 (1975) est une scientifique avec M- et M+.
- etc.
- Unico L-0832 avec M+, M-, MS, MR, √, ±, ¹/ₓ, les fonctions trigonométriques et exponentielles.
- Faber-Castell TR1 (1973)
Ça n’a l’air de rien vu qu’on trouve cette fonctionnalité sur quasiment toutes les calculatrices simples (quatre opérations) aujourd’hui. Je doute cependant qu’il y ait du monde qui comprenne et utilise cette fonctionnalité.

Muni de cette fonctionnalité supplémentaire, on va pouvoir faire les calculs précédents d’une traite …même si c’est toujours un peu longuet.
notation | compte | touches appuyées |
|---|---|---|
RPN | 6 | Clear 1 Enterꜛ 3 + 2 × |
AESH | 10 | C MC 1 + 3 = M+ 2 M× MR |
AESH | 9 | C 1 + 3 = MS 2 M× MR |
Cet exemple, (1+3)×2, utilise M× et donc n’est pas utilisable avec la TI-1250 par exemple (si on se cantonne à l’époque).
L’exemple suivant, (15+19)÷(44-7), utilise M÷ et donc n’est pas possible avec la majorité des calculatrices de l’époque qui se cantonnaient à M+ et M-. Bon, TI-50 permet, contrairement aux apparences, d’y arriver mais je doute de son usage effectif car c’était peu intuitif… (ci-après, peut-on appliquer avec confiance la séquence « ÷ RCL X↔Y » et ne pas confondre avec « ÷ X↔Y RCL » ou autre ? hum !)
notation | compte | touches appuyées |
|---|---|---|
RPN | 13 | Clear 1 5 Enterꜛ 1 9 + 4 4 Enterꜛ 7 - ÷ |
AESH | 16 | C MC 1 5 + 1 9 = M+ 4 4 - 7 = M÷ MR |
AESH | 15 | C 1 5 + 1 9 = MS 4 4 - 7 = M÷ MR |
AESP | 16 | Clear ( 1 5 + 1 9 ) ÷ ( 4 4 - 7 ) = |
TI SR-50 | 17 | C 1 5 + 1 9 = STO 4 4 - 7 = ÷ RCL X↔Y = |
Comme on le voit, ça aide pas mal …à tel point que sur HP-21 sont rajoutés des fonctions M×/M÷/M+/M-. Bien que ces touches ne soient pas présentent sur les autres modèles, la fonctionnalité est présente et sur stéroïdes ! (au lieu d’une seule mémoire de réserve, on en a neuf… ou plus…) Toujours une sacré longueur d’avance…

Mais comme on le voit, pas vraiment besoin de cette cette fonctionnalité quand on utilise une calculatrice RPN avec une pile d’au moins trois niveaux. L’exemple suivant illustre parfaitement cela.
Cet exemple se traduirait par {[(4+5)*(2+3)+6]÷(8+7)}^⁹ (où il faut bien entendu remplacer les crochets/accolades mis pour faciliter la compréhension, par des parenthèses en AESH/AESP) et se résout aussi naturellement qu’on le ferait à la main, et d’une traite sans recourir à des contournements pas évidentes.
saisie | registre X | registre Y | registre Z |
Clear | 0. | 0. | 0. |
4 | 4. | 0. | 0. |
Enterꜛ | 4. | 4. | 0. |
5 | 5. | 4. | 0. |
+ | 9. | 0. | 0. |
2 | 2. | 9. | 0. |
Enterꜛ | 2. | 2. | 9. |
3 | 3. | 2. | 9. |
+ | 5. | 9. | 0. |
× | 45. | 0. | 0. |
6 | 6. | 45. | 0. |
+ | 51. | 0. | 0. |
8 | 8. | 51. | 0. |
Enterꜛ | 8. | 8. | 51. |
7 | 7. | 8. | 51. |
+ | 15. | 51. | 0. |
÷ | 3.4 | 0. | 0. |
9 | 9. | 3.4 | 0. |
xʸ | 60716.99 | 0. | 0. |
Pour αⁿ, il fallait saisir « ⁿ α yˣ » avec la HP-35, ou « α ⁿ x≷y yˣ » si on n’a pas utilisé l’ordre attendu. Cela fait sens sur une calculatrice qui n’a pas de touche ⒑ˣ. Avec les modèles suivants (comme HP-45 et HP-21), qui ont la touche puissance ⒑, il faut saisir « α ⁿ xʸ » naturellement. Le marquage des touches est bien raccord avec ce qui est fait.
4 niveaux
HP-35 introduit un quatrième registre, de sorte à avoir deux d’accumulation (Y et Z), et celui temporaire (qui se trouve toujours en haut/dernier) est renommé T. Mais si on a rarement besoin de plus de trois niveaux, c’est un confort qui ne se refuse pas.
Pas de souci pour le numérateur, où trois niveaux sont suffisants alors que deux niveaux ne permettent pas d’y arriver d’une traite (à moins d’avoir de la mémoire de stockage.)
saisie | registre X | registre Y | registre Z |
|---|---|---|---|
Clear | 0. | 0. | 0. |
1 7 | 17. | 0. | 0. |
Enterꜛ | 17. | 17. | 0. |
4 5 | 45. | 17. | 0. |
+ | 62. | 0. | 0. |
2 | 2. | 62. | 0. |
x≷y | 62. | 2. | 0. |
yˣ | 3844. | 0. | 0. |
1 8 | 18. | 3844. | 0. |
6 7 | 67. | 18. | 3844. |
- | -49. | 3844. | 0. |
2 | 2. | -49. | 3844. |
x≷y | -49. | 2. | 3844. |
yˣ | 2401. | 3844. | 0. |
- | 1443. | 0. | 0. |
Pour le dénominateur, il faut un petit réarrangement avec une pile de trois niveaux, mais ce n’est pas suffisant…
saisie | registre X | registre Y | registre Z |
|---|---|---|---|
5 | 5. | 1443. | 0. |
Enterꜛ | 5. | 5. | 1443. |
2 | 2. | 5. | 1443. |
÷ | 2.5 | 1443. | 0. |
1 7 | 17. | 2.5 | 1443. |
…pas suffisant à moins d’enregistrer le numérateur dans la mémoire annexe pour disposer à nouveau des trois registres, or peu de constructeurs proposent cela.
saisie | registre X | registre Y | registre Z | registre S |
|---|---|---|---|---|
STO | 1443. | 0. | 0. | 1443. |
5 | 5. | 1443. | 0. | 1443. |
Enterꜛ | 5. | 5. | 443. | 1443. |
2 | 2. | 5. | 443. | 1443. |
÷ | 2.5 | 1443. | 0. | 1443. |
1 7 | 17. | 2.5 | 1443. | 1443. |
Enter | 17. | 17. | 2.5 | 1443. |
7 | 7. | 17. | 2.5 | 1443. |
÷ | 2.43 | 2.5 | 0. | 1443. |
- | 0.071 | 0. | 0. | 1443. |
CHS | -0.071 | 0. | 0. | 1443. |
1 4 | 14. | -0.071 | 0. | 1443. |
c’était là la réécriture | ||||
+ | 13.93 | 0. | 0. | 1443. |
1 2 | 12. | 13.93 | 0. | 1443. |
CHS | -12. | 13.93 | 0. | 1443. |
÷ | -1.16 | 0. | 0. | 1443. |
RCL | 1443. | -1.16 | 0. | 1443. |
x≷y | -1.16 | 1443. | 0. | 1443. |
÷ | -1243.2 | 0. | 0. | 1443. |
Avec la même réorganisation (calculer d’abord la partie droite du numérateur du dénominateur), mais en utilisant un pile de quatre niveaux, plus besoin de faire appel à la mémoire annexe.
saisie | registre X | registre Y | registre Z | registre T |
|---|---|---|---|---|
5 | 5. | 1443. | 0. | 0. |
Enterꜛ | 5. | 5. | 1443. | 0. |
2 | 2. | 5. | 1443. | 0. |
÷ | 2.5 | 1443. | 0. | 0. |
1 7 | 17. | 2.5 | 443. | 0. |
Enter | 17. | 17. | 2.5 | 1443. |
7 | 7. | 17. | 2.5 | 1443. |
÷ | 2.43 | 2.5 | 1443. | 1443. |
- | 0.071 | 1443. | 1443. | 1443. |
CHS | -0.071 | 1443. | 1443. | 1443. |
1 4 | 14. | -0.071. | 1443. | 1443. |
+ | 13.93 | 1443. | 1443. | 1443. |
1 2 | 12. | 13.93 | 1443. | 1443. |
CHS | -12. | 13.93 | 1443. | 1443. |
÷ | -1.16 | 1443. | 1443. | 1443. |
x≷y | -1.16 | 1443. | 1443. | 1443. |
÷ | -1243.2 | 1443. | 1443. | 1443. |
Si de plus, on stocke le numérateur dans la mémoire annexe, en ayant une pile de quatre niveaux on peut calculer le dénominateur sans réécriture (en saisissant les nombres tels qu’ils se présentent.) Comme aucune des autres calculatrices RPN ne propose à la fois quatre niveaux (c’est deux pour les moins chères et trois pour les plus évoluées) et la mémoire annexe (on la retrouve sur quelques modèles scientifiques mais pas toujours), on comprend que HP ai tenu la dragée haute aux compétiteurs.
On peut tester les exemples sans avoir la machine physique, en utilisant le simulateur JavaScript original de Neil Fraser, recommandé par Don C un ancien de chez TI, ou avec le correctif de Hans Klaver.
Sur Android, j’utilise plutôt RpnCalc de Edward Falk qui a les fonctions communes aux 25/27/55 (c’est le système de mémoire de ce dernier qui est usité), une pile quatre niveaux conforme tout en affichant les quatre registres comme les calculatrices de bureau de 1968. (Attention à ne pas le confondre avec le RPNcalc par Alexei Pesic qui est très bien aussi mais est moins fournie.) Sinon, il y a aussi go21 de Olivier De Smet (fonctionne assez bien chez moi, jusqu’à la mise à jour de juin 2022) et go35 du même auteur (non testé) qui permettent d’être en situation réelle.
Avec une pile de quatre niveaux, on peut juste prendre ici les termes tels qu’ils se présentent, ce qui est plus confortable.
mémoire temporaire
Les plus attentifs remarquent le comportement particulier du registre temporaire (Z pour la pile à trois niveaux, et T pour la pile à quatre niveaux) chez HP (il n’est pas garanti de retrouver ce comportement chez les autres constructeurs…) En effet, son contenu est poussé dans le niveau libéré chaque fois qu’on dépile (i.e. quand des opérations libèrent un niveau supérieur.) C’est fait à dessin pour permettre une petite automatisation sur les calculatrices de poche (avant qu’elles ne soient programmable) et pour faciliter la programmation sur les calculatrices de bureau.
Ce comportement est essentiellement mis à profit pour calculer les termes successifs d’une suite simple définie par récurrence. Ainsi, si par exemple on dépose 60 € sur un compte rémunéré à 4 % on va commencer par saisir ce taux de rémunération et le dupliquer autant de fois qu’il y a de niveaux (trois ou quatre selon le cas.)
saisie | registre X | registre Y | registre Z | registre T |
|---|---|---|---|---|
Clear | 0. | 0. | 0. | 0. |
1 . 0 4 | 1.04 | 0. | 0. | 0. |
Enterꜛ | 1.04 | 1.04 | 0. | 0. |
Enterꜛ | 1.04 | 1.04 | 1.04 | 0. |
Enterꜛ | 1.04 | 1.04 | 1.04 | 1.04 |
Comme déjà dit, La touche Enterꜛ créé une copie de X dans Y, après avoir copié Z dans T et Y dans Z : on pousse par le haut et c’est transparent pour l’usager de la calculatrice. Inversement, quand X et Y sont consommés par un calcul, dont le résultat est placé dans X, Y accueille l’ancien contenu de Z et Z celui de T : la pile redescend naturellement. La petite subtilité chez HP, est que comme il n’y a rien au delà, bah rien n’affecte le contenu du registre T qui pousse donc toujours son contenu tel une fontaine.
Donc après avoir placé la raison de la suite à tous les niveaux, il faut placer le premier terme puis on peut obtenir les suivants.
an | saisie | X | Y | Z | T |
|---|---|---|---|---|---|
0 | 6 0 | 60.00 | 1.04 | 1.04 | 1.04 |
1 | × | 60.40 | 1.04 | 1.04 | 1.04 |
2 | × | 64.90 | 1.04 | 1.04 | 1.04 |
3 | × | 67.49 | 1.04 | 1.04 | 1.04 |
4 | × | 70.19 | 1.04 | 1.04 | 1.04 |
5 | × | 73.00 | 1.04 | 1.04 | 1.04 |
6 | × | 75.92 | 1.04 | 1.04 | 1.04 |
Petit bémol cependant, les calculs trigonométriques de la HP-35 débordent aussi dessus. Le souci est corrigé avec les modèles suivants, (en allouant plus de puces mémoires dédiées aux calculs en interne) et toute la pile de quatre niveaux est laissée aux usagers.

jeu set et match
Illustration avec le fameux calcul de Mach en RPN (qui, je le rappelle, n’est pas exclusif aux calculatrices de chez Hewlett-Packard)
Quand on est habitué à faire du calcul à la main, ou au moins à les poser, on repère deux groupes par lesquels on peut commencer. On va débuter par celui de gauche, pour garder l’ordre normal de lecture.
Pour cette sous-expression, on peut continuer comme on le ferait manuellement, en calculant d’abord la parenthèse la plus interne puis en remontant vers la plus externe (et c’est ma façon de faire, on se refait pas)
saisie | affichage X | contenu Y | contenu Z | contenu T |
|---|---|---|---|---|
Clear |
| 0. | 0. | 0. |
3 5 0 |
| 0. | 0. | 0. |
Enterꜛ |
| 350. | 0. | 0. |
6 6 1 . 5 |
| 350. | 0. | 0. |
÷ |
| 0. | 0. | 0. |
2 |
| 0.5291005291 | 0. | 0. |
yˣ |
| 0. | 0. | 0. |
. 2 |
| 0.27994736989 | 0. | 0. |
× |
| 0. | 0. | 0. |
1 |
| 0.5598947397 | 0. | 0. |
+ |
| 0. | 0. | 0. |
3 . 5 |
| 1.5598947398 | 0. | 0. |
yˣ |
| 0. | 0. | 0. |
1 |
| 1.21006461734 | 0. | 0. |
- |
| 0. | 0. | 0. |
Cela illustre bien le fait qu’on peut arriver à faire des calculs complexes avec seulement trois registres, encore que nous n’en avons utilisé que deux ici (donc le minimum syndicale.)
Au tour de l’autre sous-expression à droite maintenant.
Ici aussi, je vais procéder de la parenthèse interne vers la parenthèse externe.
saisie | affichage X | contenu Y | contenu Z | contenu T |
|---|---|---|---|---|
| 0. | 0. | 0. | |
6 . 8 7 5 |
| 0.21006461733 | 0. | 0. |
Enterꜛ |
| 6.875 | 0.21006451733 | 0. |
6 |
| 6.875 | 0.21006451733 | 0. |
CHS |
| 6.875 | 0.21006451733 | 0. |
⒑ˣ |
| 6.875 | 0.21006451733 | 0. |
× |
| 0.21006461733 | 0. | 0. |
2 5 5 0 0 |
| 6.875E-6 | 0.21006451733 | 0. |
× |
| 0.21006461733 | 0. | 0. |
CHS |
| 0.21006461733 | 0. | 0. |
1 |
| -0.1753125 | 0.21006451733 | 0. |
+ |
| 0.21006461733 | 0. | 0. |
5 . 2 6 5 6 |
| 0.8246875 | 0.21006451733 | 0. |
CHS |
| 0.8246875 | 0.21006451733 | 0. |
yˣ |
| 0.21006461733 | 0. | 0. |
Là il a fallu une pile de trois niveaux, mais seulement deux pour effectuer le calcul (comme j’aime) et le troisième pour garder le résultat précédent.
Au passage, on est passé par une saisie un peu plus longue à un moment, pour avoir le plaisir de voir la nouvelle touche ⒑ˣ en action.
Jusque là, rien de compliqué …il me semble ? Maintenant, il n’y a plus qu’à terminer le calcul devenu :
…dont on prendra enfin la racine carré du quintuple. Suivant le principe adopté jusqu’à présent on fait simplement :
saisie | affichage X | contenu Y | contenu Z | contenu T |
|---|---|---|---|---|
| 0.21006461733 | 0. | 0. | |
× |
| 0. | 0. | 0. |
1 |
| 0.57961468478 | 0. | 0. |
+ |
| 0.57961468478 | 0. | 0. |
. 2 8 6 |
| 1.57961468478 | 0. | 0. |
yˣ |
| 0. | 0. | 0. |
1 |
| 1.13968709974 | 0. | 0. |
- |
| 0. | 0. | 0. |
5 |
| 0.13968709975 | 0. | 0. |
× |
| 0. | 0. | 0. |
en mémoire | 0.69843549867 | |||
√ |
| 0. | 0. | 0. |
en mémoire | 0.83572453516 | |||
Et voilà. Encore une fois, on est aux commandes (on choisi et arrange l’ordre de traitement) et c’est transparent (les résultats intermédiaires ne sont pas masqués), contrairement aux boîtes noires si on arrive à ne pas se mélanger dans les parenthèses et qu’il n’y ait pas de règles imposées (comme vue précédemment.) Ci-après, la formule donnée par le manuel de HP-85 (et dont la saisie serait similaire sur Sharp PC-1350 ou sur HP-48)
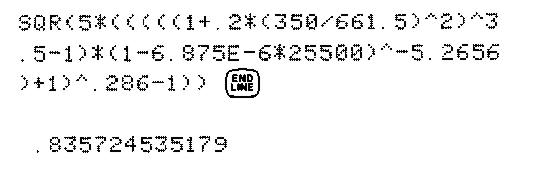
Il se trouve que de tels calculs sont légions sur certains projets où on n’avait pas l’assistance des ordinateurs à l’époque, et ce n’était pas avec des TI que j’y arrivait d’une traite (ce sont des nombres de Reynolds hydrodynamiques qui ont fini de me convertir au RPN.) Et sur des journées courtes et chargées, rien que le gain en saisie était appréciable quand on en avait une petite dizaine comme ça dans la journée. Pour revenir au cas du transsonique, y a pas photo :
| type | compte | note |
|---|---|---|
| RPN | 59 | pour 52 symboles pour les opérandes et les opérateurs |
| AESP | 76 | pour les 7 paires de parenthèses/crochets/… en plus |
Au passage, ce genre de formule n’était et n’est pas donnée sous la forme parenthésée d’une seule ligne, mais bien sous sa vraie forme mathématique/spatiale, comme :
où, ici : Hₚ et Vc sont la pression d’altitude en pied et la vitesse d’air calibrée, tandis que aₛₛₗ est la vitesse standard du son au niveau de la mer. Un exemple d’usage parmi d’autres.
Alors qu’aucune calculatrice de l’époque ne savait faire de telles opérations d’une traite, et que les concurrents en faisaient des tonnes pour moins que ça, je ne comprend pas qu’on puisse se dire choqué que l’entreprise affiche le type de calcul que savent faire ses calculatrices le doigt dans le nez. C’est par contre choquant, pour moi, de vouloir mettre une prouesse d’une époque en regard d’une banalité advenue longtemps après. L’honnêteté du procédé me semble fort douteux. Mettons cela sur le compte du manque de recul et non de quelque intention.
Et toi, agrume, savais-tu tout cela ? Et aurais-tu conçu une argumentation étrange pour taper sur une bécane qui n’est pas à ton goût ? Es-tu arrivé à faire autant avec les machines des autres marques (sans tricher bien sûr, faut pas comparer un truc de 2022 avec un truc de 1975…)
Historique des mises à jour :
- juillet 2022
- Publication initiale sur LinuxFr.org avec ajout d’illustrations et de sous-sections.
- octobre 2022
- Importation sur ZdS pour bénéficier de la richesse de zmarkdown et avoir un contenu plus lisible.
- Introduction et conclusion réadaptées en conséquence. Passage des formules de l’ASCII-art à
- novembre 2022
- Import des images d’illustration dans la galerie Zds et correction des liens en conséquence.
- décembre 2022
- Utilisation d’images réduite avec affichage en taille réelle au clic. Correction de typos.
- septembre 2023
- Correction de fautes/typos.