Savoir si le point est à gauche ou à droite d'un vecteur

Le problème d'être un avion c'est ça !

Le problème exposé dans ce sujet a été résolu.

Bonjour,

L’heure est grave mes amis ! Comme vous le savez, je suis un avion. Et ce matin, je viens de casser mon pilote automatique. :'( Je dois donc être capable de savoir mathématiquement à l’aide de mon radar (un plan en 2D) et de ma trajectoire (vecteur AB) si un objet non identifié (point OVNI) est à ma droite ou à ma gauche, pour que je puisse m’éloigner comme il le faut.

Je cherche une piste avec mon maigre niveau en géométrie, pour savoir comment identifier ma gauche et ma droite mathématiquement et savoir où se trouve l’OVNI ?

J’ai essayé de nombreuses choses mais selon l’inclinaison je n’avais que deux des trois tests ci-dessous correctes.

TESTS :

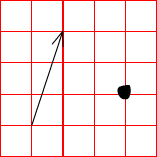
J’ai un point A(1;1)A(1;1) et un point B(2;4)B(2;4) qui forme le vecteur AB⃗(+1;+3)\vec{AB}(+1;+3) et je souhaite savoir de quel côté est le point OVNI(4;2)\mathrm{OVNI(4;2)} (SOLUTION: DROITE).

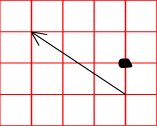
Ou au contraire : A(4;1)A(4;1), B(1;3)B(1;3) donc AB⃗(−3;+2)\vec{AB}(-3;+2) et le point OVNI(4;2)\mathrm{OVNI(4;2)} (SOLUTION: DROITE). (<— ce cas là, a brisé tous mes modèles :colere: ).

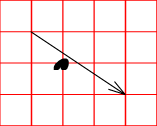
Et : A(1;3)A(1;3), B(4;1)B(4;1) donc AB⃗(+3;−2)\vec{AB}(+3;-2) et le point OVNI(2;1)\mathrm{OVNI(2;1)} (SOLUTION: DROITE).

Bon vol,

A.

+0 -0

Il te suffit de calculer le produit vectoriel entre AB→\overrightarrow{AB} et AOvni→\overrightarrow{AO_{vni}}. Le signe du produit te donne la droite ou la gauche.

Vael

@Vael, c’est quoi le signe d’un produit vectoriel ?

Au début j’pensais que tu parlais de produit scalaire alors j’a essayé… Mais c’était pas concluant (droite, gauche, droite) alors que la correction donne (droite, droite, droite).

Alors j’ai vérifier avec le produit vectoriel mais ça donne rien d’interessant ?! :euh:

J’ai tenu à verifier le corriger par tracer… Voilà mes tests :

Premier OVNI

A
A
AB→⋅AOovni→=(13).(42)=4+6=10\overrightarrow{AB}\;\cdot\;\overrightarrow{AO_{ovni}} = \begin{pmatrix} 1 \\ 3 \end{pmatrix}.\begin{pmatrix} 4 \\ 2 \end{pmatrix} = 4 + 6 =10
AB→∧AOovni→=(13)∧(42)=(12−22−12)=(10−10)\overrightarrow{AB}\;\wedge\;\overrightarrow{AO_{ovni}} = \begin{pmatrix} 1 \\ 3 \end{pmatrix}\wedge\begin{pmatrix} 4 \\ 2 \end{pmatrix} =\begin{pmatrix} 12-2 \\ 2-12 \end{pmatrix} = \begin{pmatrix} 10 \\ -10 \end{pmatrix}

Deuxième OVNI

B
B
AB→.AOovni→=(−32).(42)=−12+4=−8\overrightarrow{AB}\;.\;\overrightarrow{AO_{ovni}} = \begin{pmatrix} -3 \\ 2 \end{pmatrix}.\begin{pmatrix} 4 \\ 2 \end{pmatrix} = -12 + 4 = -8
AB→∧AOovni→=(−32)∧(42)=(8+6−6−8)=(14−14)\overrightarrow{AB}\;\wedge\;\overrightarrow{AO_{ovni}} = \begin{pmatrix} -3 \\ 2 \end{pmatrix}\wedge\begin{pmatrix} 4 \\ 2 \end{pmatrix} =\begin{pmatrix} 8+6 \\ -6-8 \end{pmatrix} = \begin{pmatrix} 14 \\ -14 \end{pmatrix}

Troisième OVNI

C
C
AB→.AOovni→=(3−2).(21)=6−2=4\overrightarrow{AB}\;.\;\overrightarrow{AO_{ovni}} = \begin{pmatrix} 3 \\ -2 \end{pmatrix}.\begin{pmatrix} 2 \\ 1 \end{pmatrix} = 6 -2 = 4
AB→∧AOovni→=(3−2)∧(21)=(−4−33+4)=(−77)\overrightarrow{AB}\;\wedge\;\overrightarrow{AO_{ovni}} = \begin{pmatrix} 3 \\ -2 \end{pmatrix}\wedge\begin{pmatrix} 2 \\ 1 \end{pmatrix} = \begin{pmatrix} -4-3 \\ 3+4 \end{pmatrix}= \begin{pmatrix} -7 \\ 7 \end{pmatrix}
+0 -0

Humm, c’est le déterminant qu’il faut calculer. Pas le produit scalaire, ni vectoriel (c’est bizarre le produit vectoriel).

Aussi, Blackline, tes vecteurs AOAO sont cassés.

J’ai repris le format de Blackline <3

Premier OVNI

A
A
det⁡(AB→,AOovni→)=det⁡((13),(31)=1∗1−3∗3=−8\det(\overrightarrow{AB}\;, \;\overrightarrow{AO_{ovni}}) = \det( \begin{pmatrix} 1 \\ 3 \end{pmatrix}, \begin{pmatrix} 3 \\ 1 \end{pmatrix} = 1*1 - 3*3 = -8

Deuxième OVNI

B
B
det⁡(AB→,AOovni→)=det⁡((−32),(01))=(−3)∗1−0=−3\det(\overrightarrow{AB}\;, \;\overrightarrow{AO_{ovni}}) = \det( \begin{pmatrix} -3 \\ 2 \end{pmatrix}, \begin{pmatrix} 0 \\ 1 \end{pmatrix}) = (-3)*1 - 0 = -3

Troisième OVNI

C
C
AB→.AOovni→=det⁡((3−2),(1−1))=−3−(−2)=−1\overrightarrow{AB}\;.\;\overrightarrow{AO_{ovni}} = \det( \begin{pmatrix} 3 \\ -2 \end{pmatrix}, \begin{pmatrix} 1 \\ -1 \end{pmatrix}) = -3 - (-2) = -1

Edit: Remarque, tes tests ne me semblent pas exhaustifs car avec le produit scalaire, ça marche aussi x) Dans les trois cas, il me semble positif (je peux me planter).

Un cas cassant le produit scalaire est le deuxième ovni dont on a inverser la direction de la deuxième composante.

det⁡(AB→,AOovni→)=det⁡((−3−2),(01))=(−3)∗1−0∗(−2)=−3\det(\overrightarrow{AB}\;, \;\overrightarrow{AO_{ovni}}) = \det( \begin{pmatrix} -3 \\ -2 \end{pmatrix}, \begin{pmatrix} 0 \\ 1 \end{pmatrix}) = (-3)*1 - 0*(-2) = -3

Alors qu’avec le produit scalaire :

AB→⋅AOovni→=(−3−2)⋅(01)=(−3)∗0+1∗(−2)=−2\overrightarrow{AB}\;\cdot\;\overrightarrow{AO_{ovni}} = \begin{pmatrix} -3 \\ -2 \end{pmatrix}\cdot\begin{pmatrix} 0 \\ 1 \end{pmatrix} = (-3)*0 + 1*(-2) = -2

Dernier truc, normalement le déterminant te donne l’air du parallélogramme formé par les deux vecteurs, le signe étant l’orientation de l’angle orienté (positif = sens trigo).

Voilà voilou. Bonne journée. ^^

+2 -0

Humm, c’est le déterminant qu’il faut calculer. Pas le produit scalaire, ni vectoriel (c’est bizarre le produit vectoriel).

En fait ça revient au même. Je pense que par « signe du produit vectoriel » il voulait dire ajouter un 3ème axe au repère pour former un espace et observer le signe de la côte du produit vectoriel, ce qui correspond au détetminant des deux vecteurs dans le plan.

Edit: Remarque, tes tests ne me semblent pas exhaustifs car avec le produit scalaire, ça marche aussi x) Dans les trois cas, il me semble positif (je peux me planter).

ache

Les tiens ne le sont pas vraiment non plus, d’ailleurs si tu regardes un peu tes exemples tu ne testes que des cas où l’objet est à droite.

Avec un point A en (0, 0), B en (3, -10) et OVNI en (1, 1) (donc à droite), tu devrais voir que le résultat avec le déterminant est bon, alors que le produit scalaire ne donne rien d’exploitable.

+3 -0

Je crois que tu as un soucis avec tes produits vectoriels @Blackline , Le produit vectoriel de deux vecteurs donne un vecteur perpendiculaire au plan formé par les deux vecteurs. Ici comme on est dans le plan ça donne un vecteur avec une unique composante en z, composante égale au déterminant des deux vecteurs.

+2 -0

Ok donc je dois partir la dessus : http://paquito.amposta.free.fr/glossd/determin.htm ?

det(A⃗,B⃗)=Ax∗By−Ay∗Bx\cancel{\text{det}(\vec{A}, \vec{B}) = A_x*B_y - A_y*B_x}

EDIT :

det(A⃗,B⃗)=AB⃗x∗AO⃗y−AB⃗y∗AO⃗x\text{det}(\vec{A}, \vec{B}) = \vec{AB}_x*\vec{AO}_y - \vec{AB}_y*\vec{AO}_x
+0 -0

Ça marche ! Merci ! :D

En bonus :
function hasOVNIinTheFlightPlan(OVNI) {
    for (let i = 0, A, B; i < borders.length; i++) {
        A = borders[i];
        B = borders[i+1] || borders[0];
        let ABx = A.x - B.x,
            ABy = A.y - B.y,
            AOx = A.x - OVNI.x,
            AOy = A.y - OVNI.y,
            det = ABx*AOy - AOx*ABy;

        if (det < 0)
            return false;
    }
    return true;
}
+1 -0

a = résultat du produit vectoriel, (signe de la 3ème composante)

b = résultat du produit scalaire.

a peut être positif ou négatif, b peut-être positif ou négatif. Soit 4 commbinaisons. Ces 4 combinaisons corespondent aux 4 cadrants : 0°-90° , 90°-180° , 180°-270° et 270°-360°.

Et bien entendu , si a ou b est nul, on est dans les cas limites (ovni droit devant, droit derrière …)

+0 -0

@ache, Si tu te places en A et que tu regardes vers B, OVNI peut être soit devant toi soit derrière. Le signe du produit scalaire te permet de le savoir (car il correspond à la colinéarité du projeté orthogonal d’un vecteur sur l’autre)1.

  1. Je sais pas si j’utilise les bons termes car la « projection orthogonale sur un vecteur » ça ne me semble pas très formel, mais c’est l’idée.

    ↩
+0 -0

Oui dsl. Le produit vectoriel en 2D donne nécessairement un vecteur selon l’axe OzOz. Ce vecteur pourra s’écrire λz⃗\lambda \vec{z}. Je parlais donc du signe de λ\lambda.

edit : yep rigoureusement c’est le déterminant en effet, mais comme en 2D c’es equivalent… :-° ( se ratrappe en aux branches )

+0 -0

yep rigoureusement c’est le déterminant en effet, mais comme en 2D c’es equivalent

Pas qu’en 2D, en 3D aussi, puisque dans une base orthonormée directe

a×b=det⁡(e1e2e3a1a2a3b1b2b3)a\times b= \det\begin{pmatrix} \boldsymbol e_1 & \boldsymbol e_2 & \boldsymbol e_3\\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3\\ \end{pmatrix}

C’est plus une notation qu’autre chose, mais ça montre qu’un produit vectoriel va voir le déterminant des projetés des vecteurs dans les trois plans perpendiculaires aux vecteurs de base.

D’ailleurs perso ça m’a pas choqué quand tu as parlé du signe du produit vectoriel, on fait cet abus tout le temps quand on bosse dans un plan.

+0 -0

@Lucas-84 Tu fais bien d’en parler, à l’initialisation de borders, j’ai glissé à la fin un :

    borders.push(borders[0])

D’ailleurs on pourrait se passer de cette ligne en remplaçant la ligne 4 de mon code ci-dessus par :

    B = borders[i+1]||borders[0];

Cet algo est limité en effet 😔

Il faudra que j’essaye celui des collisions pairs et impaires.

+0 -0

Mais t’es sûr que ça devrait pas être i < border.length-1 quand même ? Je sais pas trop ce que c’est comme langage mais ça m’a l’air suspect sinon.

Tout dépend de ce que tu cherches à faire, si tous tes polygones sont convexes, c’est une excellente manière de faire (beaucoup plus simple que l’histoire des collisions, même si y a une fameuse manière de faire tenir ça en 7 lignes).

+0 -0

Le dernier terme c’est borders[borders.length-1] car l’index commence à zéro et non 1.

Donc :

Pour ABCD -> 4

  • AB
  • BC
  • CD
  • DA

Le borders.push(borders[0]) n’était pas une si bonne idée. Dans ma précipitation pour vous partager le code, j’ai remplacé la variable N qui était dans la boucle for par borders.length mais N est une valeur antérieure de borders.length avant borders.push(borders[0]) donc N valait borders.length - 1 mais en modifiant la ligne 6, le problème ne se pose pas.

Donc au lieu d’ajouter une variable N ou -1 qui est plus complexe pour la lecture, je rajoute une ligne 6.

+0 -0
Connectez-vous pour pouvoir poster un message.
Connexion

Pas encore membre ?

Créez un compte en une minute pour profiter pleinement de toutes les fonctionnalités de Zeste de Savoir. Ici, tout est gratuit et sans publicité.
Créer un compte