Merci pour votre réponse.
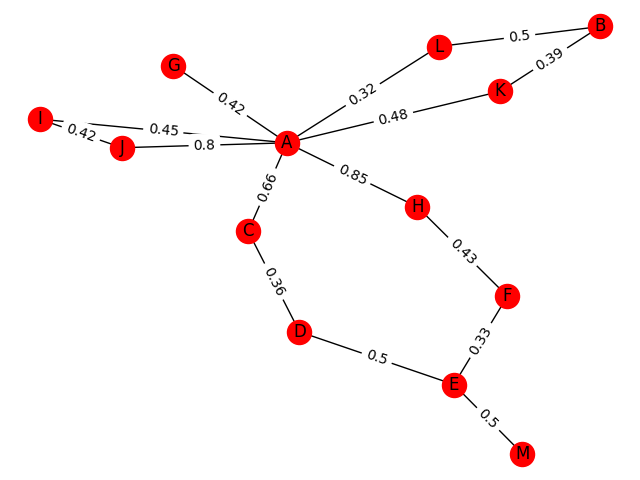
Nous avons saisi une matrice d’adjacence pour un exemple réel de graphe.
En changeant "m_adjac" (l.22), on obtient toujours une distance et un chemin mais il ne correspondent pas aux résultats attendus. Le chemin proposé relie par exemple des sommets qui ne sont pas reliés. Je n’arrive pas a vous joindre la photo du graphe en revanche, voici notre code sur Python:
Nvilles = 13
L0 = [0,0.5,0,0,0,0,0,0,0,0,0,0,0]
L1 = [0.5,0,0.5,0.33,0,0,0,0,0,0,0,0,0]
L2 = [0,0.5,0,0,0.36,0,0,0,0,0,0,0,0]
L3 = [0,0.33,0,0,0,0.43,0,0,0,0,0,0,0]
L4 = [0,0,0.36,0,0,0,0,0,0,0.66,0,0,0]
L5 = [0,0,0,0.43,0,0,0,0,0,0.85,0,0,0]
L6 = [0,0,0,0,0,0,0,0,0.42,0.45,0,0,0]
L7 = [0,0,0,0,0,0,0,0,0,0.42,0,0,0]
L8 = [0,0,0,0,0,0,0.42,0,0,0.8,0,0,0]
L9 = [0,0,0,0,0.66,0.85,0.45,0.42,0.8,0,0.48,0.32,0]
L10 = [0,0,0,0,0,0,0,0,0,0.48,0,0,0.39]
L11 = [0,0,0,0,0,0,0,0,0,0.32,0,0,0.5]
L12 = [0,0,0,0,0,0,0,0,0,0,0.39,0.5,0]
m_adjac = [L0,L1,L2,L3,L4,L5,L6,L7,L8,L9,L10,L11,L12]
DIJ=list()
for i in range (Nvilles):
DIJ.append([1000000,"X","N"])
ville_select=0
dist_interm=0
while ville_select != Nvilles-1:
minimum=1000000
for n in range(1,Nvilles):
if DIJ[n][2]=="N":
dist=m_adjac[ville_select][n]
dist_totale=dist_interm+dist
if dist != 0 and dist_totale < DIJ[n][0]:
DIJ[n][0]=dist_totale
DIJ[n][1]=ville_select
if DIJ[n][0]<minimum:
minimum=DIJ[n][0]
pville_select=n
ville_select=pville_select
DIJ[ville_select][2]="O"
dist_interm=DIJ[ville_select][0]
for i in range(1,Nvilles):
print (DIJ[i])
print ("\n")
chemin=list()
ville=Nvilles-1
chemin.append(ville)
while ville != 0:
ville=DIJ[ville][1]
chemin.append(ville)
print ("plus court chemin, à lire à l'envers : ",chemin)
print ("distance totale : ",DIJ[Nvilles-1][0])
On obtient dans la console:
[0.5, 0, 'O']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[0.5, 0, 'O']
[1.0, 1, 'N']
[0.8300000000000001, 1, 'O']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[0.5, 0, 'O']
[1.0, 1, 'O']
[0.8300000000000001, 1, 'O']
[1000000, 'X', 'N']
[1.26, 3, 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[0.5, 0, 'O']
[1.0, 1, 'O']
[0.8300000000000001, 1, 'O']
[1.3599999999999999, 2, 'N']
[1.26, 3, 'O']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[0.5, 0, 'O']
[1.0, 1, 'O']
[0.8300000000000001, 1, 'O']
[1.3599999999999999, 2, 'O']
[1.26, 3, 'O']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[2.11, 5, 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[0.5, 0, 'O']
[1.0, 1, 'O']
[0.8300000000000001, 1, 'O']
[1.3599999999999999, 2, 'O']
[1.26, 3, 'O']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[2.02, 4, 'O']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[1000000, 'X', 'N']
[0.5, 0, 'O']
[1.0, 1, 'O']
[0.8300000000000001, 1, 'O']
[1.3599999999999999, 2, 'O']
[1.26, 3, 'O']
[2.47, 9, 'N']
[2.44, 9, 'N']
[2.8200000000000003, 9, 'N']
[2.02, 4, 'O']
[2.5, 9, 'N']
[2.34, 9, 'O']
[1000000, 'X', 'N']
[0.5, 0, 'O']
[1.0, 1, 'O']
[0.8300000000000001, 1, 'O']
[1.3599999999999999, 2, 'O']
[1.26, 3, 'O']
[2.47, 9, 'N']
[2.44, 9, 'O']
[2.8200000000000003, 9, 'N']
[2.02, 4, 'O']
[2.5, 9, 'N']
[2.34, 9, 'O']
[2.84, 11, 'N']
[0.5, 0, 'O']
[1.0, 1, 'O']
[0.8300000000000001, 1, 'O']
[1.3599999999999999, 2, 'O']
[1.26, 3, 'O']
[2.47, 9, 'O']
[2.44, 9, 'O']
[2.8200000000000003, 9, 'N']
[2.02, 4, 'O']
[2.5, 9, 'N']
[2.34, 9, 'O']
[2.84, 11, 'N']
[0.5, 0, 'O']
[1.0, 1, 'O']
[0.8300000000000001, 1, 'O']
[1.3599999999999999, 2, 'O']
[1.26, 3, 'O']
[2.47, 9, 'O']
[2.44, 9, 'O']
[2.8200000000000003, 9, 'N']
[2.02, 4, 'O']
[2.5, 9, 'O']
[2.34, 9, 'O']
[2.84, 11, 'N']
[0.5, 0, 'O']
[1.0, 1, 'O']
[0.8300000000000001, 1, 'O']
[1.3599999999999999, 2, 'O']
[1.26, 3, 'O']
[2.47, 9, 'O']
[2.44, 9, 'O']
[2.8200000000000003, 9, 'O']
[2.02, 4, 'O']
[2.5, 9, 'O']
[2.34, 9, 'O']
[2.84, 11, 'N']
[0.5, 0, 'O']
[1.0, 1, 'O']
[0.8300000000000001, 1, 'O']
[1.3599999999999999, 2, 'O']
[1.26, 3, 'O']
[2.47, 9, 'O']
[2.44, 9, 'O']
[2.8200000000000003, 9, 'O']
[2.02, 4, 'O']
[2.5, 9, 'O']
[2.34, 9, 'O']
[2.84, 11, 'O']